Web of trust

This site is most likely a scam. If you suddenly find an unjustified and incorrect review, such as your website being labelled as a paid per click advertising site, they will not remove the review. Instead they will ask you to register with them and claim the site as the site owner. This involves inserting a piece of code into your website that they can then monitor for whatever reason. Scams like this are all too often used to to increase their "member" numbers, which can then potentially be sold to advertisers or email mail farmers. The reviews are most likely made by a bot.

Around 4,241,223 reviews have been added by a superhuman member called GURBL who has been a member since 2010. That's a staggering 68,406 reviews per month, or 2,280 reviews per day. To spend that much time in front of a computer GURBL would need to be a total computer geek, allowing for the average time spent masturbating daily by a computer geek that amount of 'reviewing' would not be possible. It is therefore entirely likely GURBL is a bot.

In light of their appauling service towards site owners and prospective customers, anyone with sense would not trust this company if they said it was dark at midnight.

Beware, do not fall for this scam

In cryptography, a web of trust is a concept used in PGP, GnuPG, and other OpenPGP-compatible systems to establish the authenticity of the binding between a public key and its owner. Its decentralized trust model is an alternative to the centralized trust model of a public key infrastructure (PKI), which relies exclusively on a certificate authority (or a hierarchy of such). As with computer networks, there are many independent webs of trust, and any user (through their identity certificate) can be a part of, and a link between, multiple webs.

The web of trust concept was first put forth by PGP creator Phil Zimmermann in 1992 in the manual for PGP version 2.0:

As time goes on, you will accumulate keys from other people that you may want to designate as trusted introducers. Everyone else will each choose their own trusted introducers. And everyone will gradually accumulate and distribute with their key a collection of certifying signatures from other people, with the expectation that anyone receiving it will trust at least one or two of the signatures. This will cause the emergence of a decentralized fault-tolerant web of confidence for all public keys.

Operation of a web of trust

All OpenPGP-compliant implementations include a certificate vetting scheme to assist with this; its operation has been termed a web of trust. OpenPGP identity certificates (which include public key(s) and owner information) can be digitally signed by other users who, by that act, endorse the association of that public key with the person or entity listed in the certificate. This is commonly done at key signing parties.

OpenPGP-compliant implementations also include a vote counting scheme which can be used to determine which public key – owner association a user will trust while using PGP. For instance, if three partially trusted endorsers have vouched for a certificate (and so its included public key – owner binding), OR if one fully trusted endorser has done so, the association between owner and public key in that certificate will be trusted to be correct. The parameters are user-adjustable (e.g., no partials at all, or perhaps 6 partials) and can be completely bypassed if desired.

The scheme is flexible, unlike most public key infrastructure designs, and leaves trust decision(s) in the hands of individual users. It is not perfect and requires both caution and intelligent supervision by users. Essentially all PKI designs are less flexible and require users to follow the trust endorsement of the PKI generated, certificate authority (CA)-signed, certificates. Intelligent action is normally neither required nor allowed. These arrangements are not perfect either, and require both caution and care by users.

In simpler terms, you have 2 keys: a public key that you let the people you trust know; and a private key that only you know. Your private key will decrypt any information encrypted with your public key. In the web of trust you have a key ring with a group of people's public keys.

You encrypt your information with the recipients public key, and only their private key will decrypt it. You then digitally sign the information with your private key, so when they verify it with your public key, they can confirm that it is you. Doing this will ensure that the information came from you and has not been tampered with, and only the person you are sending it to can read the information (because only they know their private key).

Contrast with typical PKI

In contrast, a typical X.509 PKI permits each certificate to be signed only by a single party: a certificate authority (CA). The CA's certificate may itself be signed by a different CA, all the way up to a 'self-signed' root certificate. Root certificates must be available to those who use a lower level CA certificate and so are typically distributed widely. They are for instance, distributed with such applications as browsers and email clients. In this way SSL/TLS-protected Web pages, email messages, etc. can be authenticated without requiring users to manually install root certificates. Applications commonly include over one hundred root certificates from dozens of PKIs, thus by default bestowing trust throughout the hierarchy of certificates which lead back to them.

Web of trust problems

The OpenPGP web of trust is essentially unaffected by such things as company failures, and has continued to function with little change. However, a related problem does occur. Users, whether individuals or organizations, who lose track of a private key can no longer decrypt messages sent to them produced using the matching public key found in an OpenPGP certificate. Early PGP certificates did not include expiry dates, and those certificates had unlimited lives. Users had to prepare a signed cancellation certificate against the time when the matching private key was lost or compromised. One very prominent cryptographer is still getting messages encrypted using a public key for which he long ago lost track of the private key (Ferguson 2003, p. 333). He can't do much with those messages except discard them after notifying the sender that they were unreadable and requesting resending with a public key for which he still has the matching private key. Later PGP, and all OpenPGP compliant certificates include expiry dates which automatically preclude such troubles (eventually) when used sensibly. This problem can also be easily avoided by the use of "designated revokers", which were introduced in the early 1990s. A key owner may designate a third party that has permission to revoke the key owner's key (in case the key owner loses his own private key and thus loses the ability to revoke his own public key).

A non-technical, social difficulty with a Web of Trust like the one built into PGP/OpenPGP type systems is that every web of trust without a central controller (e.g., a CA) depends on other users for trust. Those with new certificates (i.e., produced in the process of generating a new key pair) will not likely be readily trusted by other users' systems, that is by those they have not personally met, until they find enough endorsements for the new certificate. This is because many other Web of Trust users will have their certificate vetting set to require one or more fully trusted endorsers of an otherwise unknown certificate (or perhaps several partial endorsers) before using the public key in that certificate to prepare messages, believe signatures, etc.

Despite the wide use of OpenPGP compliant systems and easy availability of on-line multiple key servers, it is possible in practice to be unable to readily find someone (or several people) to endorse a new certificate (e.g., by comparing physical identification to key owner information and then digitally signing the new certificate). Users in remote areas or undeveloped ones, for instance, may find other users scarce. And, if the other's certificate is also new (and with no or few endorsements from others), then its signature on any new certificate can offer only marginal benefit toward becoming trusted by still other parties' systems and so able to securely exchange messages with them. Key signing parties are a relatively popular mechanism to resolve this problem of finding other users who can install one's certificate in existing webs of trust by endorsing it. Websites also exist to facilitate the location of other OpenPGP users to arrange keysignings. The Gossamer Spider Web of Trust also makes key verification easier by linking OpenPGP users via a hierarchical style web of trust where end users can benefit by coincidental or determined trust of someone who is endorsed as an introducer, or by explicitly trusting GSWoT's top-level key minimally as a level 2 introducer (the top-level key endorses level 1 introducers).

The possibility of finding chains of certificates is often justified by the "small world phenomenon": given two individuals, it is often possible to find a short chain of people between them such that each person in the chain knows the preceding and following links. However, such a chain is not necessarily useful: the person encrypting an email or verifying a signature not only has to find a chain of signatures from his private key to his correspondent's, but also to trust each person of the chain to be honest and competent about signing keys (that is, he has to judge whether these people are likely to honestly follow the guidelines about verifying the identity of people before signing keys). This is a much stronger constraint.

Doing the math

The work of Audun Jøsang is an algebraic treatment of trust measurements and methods and calculation that attempts to capture how trust varies as it "traverses" a web of trust. The other sites (below) contains a link to his publications. A good one to start with might be "An Algebra for Assessing Trust in Certification Chains". Also see Subjective logic and Trust metric.

Mean shortest distance

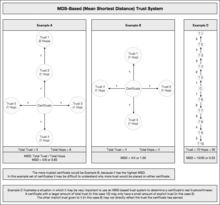
In statistical analysis of the PGP/GnuPG/OpenPGP Web of trust the mean shortest distance (MSD) is one measurement of how "trusted" a given PGP key is within the "strongly connected" set of PGP keys that make up the Web of trust.

Drew Streib wrote the following in his explanation of keyring analysis:^[1]

There are a variety of metrics one could apply to this set, but I've chosen initially to measure the "mean shortest distance" (MSD) to each key. Since every key is reachable from every other in the strong set, it is possible to find out the shortest distance (number of hops) to any given key from any other key. Averaging these distances gives the MSD to that key from every other key in the strong set.
It is desirable to have as short as possible an MSD to your key, as that means that on average, people can reach your key quickly through signatures, and thus your key is relatively more trusted than a key with a higher MSD.
NOTE: This does not mean that you should universally trust keys with a low MSD. This is merely a relative measurement for statistical purposes.
The MSD has the property of being no more than 1 higher than your lowest signature. In the worst case, every key in the strong set could reach you by getting to that key, plus 1 hop to get to you. It also encourages the joining of keys that are separated by great distances in the graph, as it will make you a highway of sorts for shortest paths between keys in those groups. In the end, it encourages an overall tightening of the world graph, shortening distances between key owners.

MSD has become a common metric for analysis of sets of PGP keys. Very often you will see the MSD being calculated for a given subset of keys and compared with the global MSD which generally refers to the keys ranking within one of the larger key analyses of the global Web of trust.

References

^ Streib, M. Drew. "Explanation of this Keyring Analysis". Archived from the original on 3 February 2009. Retrieved 13 December 2013.

Ferguson, Niels (2003). Practical Cryptography. John Wiley & Sons. ISBN 0-471-22357-3. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)

External links

An explanation of the PGP Web of Trust
"The PGP Trust Model" - by Alfarez Abdul-Rahman
analysis of the strong set in the PGP web of trust - regularly updated

[1] Streib, M. Drew. "Explanation of this Keyring Analysis". Archived from the original on 3 February 2009. Retrieved 13 December 2013.

[1]