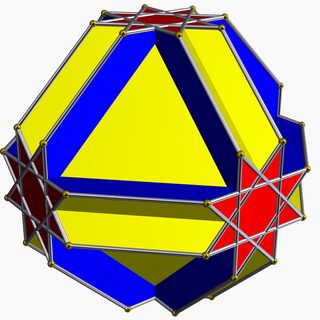
Cubitruncated cuboctahedron
| Cubitruncated cuboctahedron | |
|---|---|
| |
| Type | Uniform star polyhedron |
| Elements | F = 20, E = 72 V = 48 (χ = −4) |
| Faces by sides | 8{6}+6{8}+6{8/3} |
| Coxeter diagram |    
|
| Wythoff symbol | 3 4 4/3 | |
| Symmetry group | Oh, [4,3], *432 |
| Index references | U16, C52, W79 |
| Dual polyhedron | Tetradyakis hexahedron |
| Vertex figure |  6.8.8/3 |
| Bowers acronym | Cotco |
In geometry, the cubitruncated cuboctahedron or cuboctatruncated cuboctahedron is a nonconvex uniform polyhedron, indexed as U16.
Convex hull
Its convex hull is a nonuniform truncated cuboctahedron.
 Convex hull |
Cubitruncated cuboctahedron |
Orthogonal projection
Cartesian coordinates
Cartesian coordinates for the vertices of a cubitruncated cuboctahedron are all the permutations of
- (±(√2−1), ±1, ±(√2+1))
See also
Related polyhedra
| Tetradyakis hexahedron | |
|---|---|
| |
| Type | Star polyhedron |
| Face | 
|
| Elements | F = 48, E = 72 V = 20 (χ = −4) |
| Symmetry group | Oh, [4,3], *432 |
| Index references | DU16 |
| dual polyhedron | Cubitruncated cuboctahedron |
The tetradyakis hexahedron is a nonconvex isohedral polyhedron. It has 48 intersecting scalene triangle faces, 72 edges, and 20 vertices.
It is the dual of the uniform cubitruncated cuboctahedron.
External links
 | This polyhedron-related article is a stub. You can help Wikipedia by expanding it. |