Elongated dodecahedron
| Elongated dodecahedron | |
|---|---|
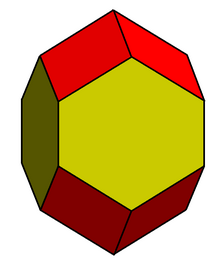 | |
| Type | Dodecahedron |
| Faces | 8 rhombi 4 hexagons |
| Edges | 28 |
| Vertices | 18 |
| Vertex configuration | (8) 4.6.6 (8) 4.4.6 (2) 4.4.4.4 |
| Symmetry group | D4h, [4,2], (*422), order 16 |
| Rotation group | D4, [4,2]+, (422), order 8 |
| Dual polyhedron | - |
| Properties | convex, parallelohedron |
| Net | |
 | |
In geometry, the elongated dodecahedron,[1] extended rhombic dodecahedron, rhombo-hexagonal dodecahedron[2] or hexarhombic dodecahedron[3] is a convex polyhedron with 8 rhombic and 4 hexagonal faces. The hexagons can be made equilateral, or regular depending on the shape of the rhombi. It can be seen as constructed from a rhombic dodecahedron elongated by a square prism. Along with the rhombic dodecahedron, it is a space-filling polyhedron.
Variations
The elongated dodecahedron can be constructed as a contraction of a uniform truncated octahedron, where square faces are reduced to single edges and regular hexagonal faces are reduced to 60 degree rhombic faces. This construction alternates square and rhombi on the 4-valence vertices, and has half the symmetry, D2h symmetry, order 8.
Tessellation
- It can tesselate all space by translations.
- It is the Wigner-Seitz cell for certain body-centered tetragonal lattices.

|

|
This is related to the rhombic dodecahedral honeycomb with an elongation of zero. Projected normal to the elongation direction, the honeycomb looks like a square tiling with the rhombi projected into squares.
See also
References
- ^ Coxeter (1973) p.257
- ^ Williamson (1979) p169
- ^ http://www.matha.mathematik.uni-dortmund.de/~thilo/contents/fedorov.htm
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. rhombo-hexagonal dodecahedron, p169
- H.S.M. Coxeter, Regular Polytopes, Third edition, (1973), Dover edition, ISBN 0-486-61480-8 p. 257

