Magnetic mirror
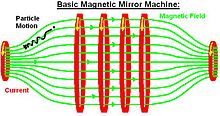
A magnetic mirror is a configuration of magnetic field lines in which a charged particle is reflected from a high density magnetic field to low density magnetic field. This mirror effect will only occur for particles within a limited range of velocity and angle of approach. Magnetic mirrors are made of specialized electromagnets designed to create a highly inhomogeneous field. Large magnetic mirrors have been used experimentally as a means of plasma confinement. One major application being researched is to confine the hot, electrically charged plasma inside a fusion reactor to generate fusion power (see magnetic confinement fusion). A category of experimental fusion reactors called mirror machines confine plasma within a magnetic field between two magnetic mirrors. The largest to be built was the Mirror Fusion Test Facility (MFTF) in 1986.
A charged particle moving within a region of magnetic field experiences a Lorentz force that causes it to move in a helical (corkscrew) path along a magnetic field line. The radius of the circle that the particle describes is called the radius of gyration or gyroradius. If it enters a region of denser magnetic field lines, a field gradient, the combination of the radial component of the fields and the azimuthal motion of the particle results in a force pointed against the gradient, in the direction of lower magnetic field. It is this force that can reflect the particle, causing it to decelerate and reverse direction.[1]
History



The concept of magnetic-mirror plasma confinement was proposed in mid-1950s independently by Gersh Budker[2] at the Kurchatov Institute, Russia and Richard F. Post[3] at the Lawrence Livermore National Laboratory. The first small-scale open magnetic plasma trap machine ("probkotron") was built in 1959 at the Budker Institute of Nuclear Physics in Novosibirsk, Russia.
By the late 1960s, magnetic mirror confinement was considered a viable technique for producing fusion energy. In the United States, еfforts were initially funded under the United States Atomic Energy Commissions' Project Sherwood. A machine design was first published in 1967.[4] The concept was advocated by Richard F. Post, Kenneth Fowler, Fred Coensgen and many others at the Lawrence Livermore National Laboratory.[5] As a result of advocacy, the cold war, and the 1970s energy crisis a massive magnetic mirror program was funded by the U.S. federal government.
This program resulted in a series of large magnetic mirror devices including: 2X,[6] Baseball I, Baseball II, the Tandem Mirror Experiment, the Tandem mirror experiment upgrade, the Mirror Fusion Test Facility and the MFTF-B.[7][8] These machines were built and tested at Livermore from the late 60's to the mid 80's.[9] A number of institutions collaborated on these machines, conducting experiments. These included the Institute for Advanced Study and the University of Wisconsin–Madison.[10][11] The last machine, the Mirror Fusion Test Facility was 372 million dollars, at that time, the most expensive project in Livermore history. It opened on February 21, 1986 and was promptly shut down. The reason given was to balance the United States federal budget.[9] This program was supported from within the Carter and early Reagan administrations by Edwin E. Kintner, a U.S. Navy captain, under Alvin Trivelpiece. Kintner resigned in 1982 complaining that the federal government had not provided the resources needed for the research.[12]
The concept had a number of technical challenges including maintaining the non-Maxwellian velocity distribution. This meant that instead of many high energy ions hitting one another, the ion energy spread out into a bell curve. The ions then thermalized, leaving most of the material too cold to fuse. Collisions also scattered the charged particles so much that they could not be contained. Lastly, velocity space instabilities contributed to the escape of the plasma.
Magnetic mirrors play an important role in other types of magnetic fusion energy devices such as tokamaks, where the toroidal magnetic field is stronger on the inboard side than on the outboard side. The resulting effects are known as neoclassical. Magnetic mirrors also occur in nature. Electrons and ions in the magnetosphere, for example, will bounce back and forth between the stronger fields at the poles, leading to the Van Allen radiation belts.
Mathematical derivation
The mirror effect can be shown mathematically. Assume adiabatic invariance of the magnetic moment, i.e. that the particle's magnetic moment and total energy do not change.[13] Adiabatic invariance is lost when a particle occupies a null point or zone of no magnetic field.[14] The magnetic moment can be expressed as:
It is assumed that μ will remain constant while the particle moves into the denser magnetic field. Mathematically, for this to happen the velocity perpendicular to the magnetic field must also rise. Meanwhile the total energy of the particle can be expressed as:
In regions with no electric field, if the total energy remains constant then the velocity parallel to the magnetic field must drop. If it can go negative then there is a motion repelling the particle from the dense fields.
Mirror ratios
Magnetic mirrors themselves have a mirror ratio this is expressed mathematically as:[15]
At the same time, particles within the mirror have a pitch angle. This is the angle between the particles' velocity vector and the magnetic field vector.[16] Surprisingly, the particles with the small pitch angle can escape the mirror.[17] These particles are said to be in the loss cone. The reflected particles meet the following criteria:[18]
Where is the particle velocity perpendicular to the magnetic field and is the particle speed.
This result was surprising because it was expected that heavier and faster particles, or those with less electric charge, would be harder to reflect. It was also expected that smaller magnetic field would reflect less particles. However, the gyroradius in those circumstances is also larger, so that the radial component of the magnetic field seen by the particle is also larger. It is true that the minimum volume and magnetic energy is larger for the case of fast particles and weak fields, but the mirror ratio required remains the same.
Adiabatic invariance
The properties of magnetic mirrors can be derived using the adiabatic invariance of magnetic flux under changes in magnetic field strength. As the field gets stronger, the velocity increases proportionally to the square root of B, and the kinetic energy is proportional to B. This can be thought of as an effective potential binding the particle.
Magnetic bottles
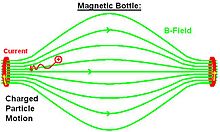
A magnetic bottle is two magnetic mirrors placed close together. For example, two parallel coils separated by a small distance, carrying the same current in the same direction will produce a magnetic bottle between them. Unlike the full mirror machine which typically had many large rings of current surrounding the middle of the magnetic field, the bottle typically has just two rings of current. Particles near either end of the bottle experience a magnetic force towards the center of the region; particles with appropriate speeds spiral repeatedly from one end of the region to the other and back. Magnetic bottles can be used to temporarily trap charged particles. It is easier to trap electrons than ions, because electrons are so much lighter[19] This technique is used to confine very hot plasmas with temperatures of the order of 106 K.
In a similar way, the Earth's non-uniform magnetic field traps charged particles coming from the sun in doughnut shaped regions around the earth called the "Van Allen radiation belts", which were discovered in 1958 using data obtained by instruments aboard the Explorer 1 satellite.
Biconic cusps

If one of the poles in the magnetic bottle is reversed, it becomes a biconic cusp, which can also hold charged particles.[20][21][22] Biconic cusps were first studied by Harold Grad at the Courant Institute, studies reveal the presence of different types of particles inside a biconic cusp.
See also
- tokamak
- Biconic cusp
- List of plasma (physics) articles
- Pitch angle (particle motion)
- Project Sherwood
- Polywell
- Harold Grad
- Mirror Fusion Test Facility
References
- ^ Fitzpatrick, Richard. "Magnetic Mirrors." Home Page for Richard Fitzpatrick. The University of Texas at Austin, 31 Mar. 2011. Web. 19 July 2011. .
- ^ In Russian: Fizika Plazmy i Problema Upravlyaemykh Termoyadernykh Reaktsii, Vol. 3, p. 1 (Moscow: Izd. AN SSSR, 1958); in English: G. I. Budker, Plasma Physics and the Problem of Controlled Thermonuclear Reactions, Vol. 3, pp. 1-33 (Pergamon Press, 1959)
- ^ R. F. Post, Proc. of Second U.N. Int. Conf. on Peaceful Uses of Atomic Energy, Vol. 32, p. 245 (Geneva, 1958)
- ^ G. G. Kelley, Plasma Phys. 2, 503 (1967)
- ^ "Mirror Systems: Fuel Cycles, loss reduction and energy recovery" by Richard F. Post, BNES Nuclear fusion reactor conferences at Culham laboratory, September 1969.
- ^ Principals of plasma physics, Nicholas Krall, 1973, Page 273
- ^ "Summary of results from the tandem mirror experiment, TMX group, February 26, 1981
- ^ "TMX Major Project proposal" Fred Coensgen, January 12, 1977
- ^ a b Booth, William. "Fusion's $372-Million Mothball." Science [New York City] 9 Oct. 1987, Volume 238 ed.: 152-55. Print.
- ^ "ion losses from end-stoppered mirror trap" D P Chernnin, nuclear fusion 18 (1978)
- ^ "Experiments in a tandem mirror sustained and heated solely by rf" R Breun, Physical Review Letters, December 21, 1981
- ^ KOPPEL, NIKO. "Edwin E. Kintner, Nuclear Power Pioneer, Dies at 90." The New York Times, Science Section. The New York Times, 20 May 2010. Web. 17 Apr. 2011. <http://www.nytimes.com/2010/05/21/science/21kintner.html?_r=1>
- ^ F. Chen, Introduction to Plasma Physics and Controlled Fusion (Plenum, New York, 1984), Vol. 1, pp. 30–34. ISBN 978-0-306-41332-2
- ^ TG Northrop, "The Adiabatic Motion of Charged Particles" (Interscience, New York, 1963)
- ^ "Particle Loss Rates from Electrostatic Wells of Arbitrary Mirror Ratios." Physics of Fluids 28.1 (1985): 352-57. Web. 15.
- ^ Dolan, T. J. "Magnetic Electrostatic Plasma Confinement." Plasma Physics and Controlled Fusion 36 (1994): 1539-593. Print.
- ^ G Gibson, Willard C Jordan, Eugene Lauer, Physical Review Letters, 5: 141 (1960)
- ^ Principals of Plasma Physics, N Krall, 1973, Page 267
- ^ "A biased probe analysis of potential well formation in an electron only, low beta Polywell magnetic field" Physics of Plasma, May 9, 2013, Vol 20, 052504
- ^ The motion of a charged particle near a zero field point (in english). New York: New York University: Courant Institute of Mathematical Sciences,. 1961.
- ^ Grad, H. Theory of Cusped Geometries, I. General Survey, NYO-7969, Inst. Math. Sci., N.Y.U., December 1, 1957
- ^ Berowitz, H Grad and H Rubin, in proceedings of the second United Nations International conference on peaceful uses of atomic energy, Geneva, 1958, Vol 31, Page 177







