Cryptographic hash function
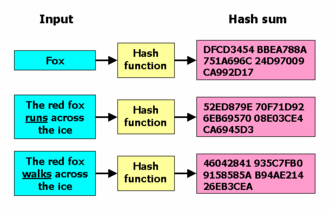
In cryptography, a cryptographic hash function is a hash function with certain additional security properties to make it suitable for use as a primitive in various information security applications, such as authentication and message integrity. A hash function takes a long string (or message) of any length as input and produces a fixed length string as output, sometimes termed a message digest or a digital fingerprint.
In various standards and applications, the two most-commonly used hash functions are MD5 and SHA-1. In 2005, security flaws were identified in both algorithms.
Overview
Broadly speaking, a cryptographic hash function should behave as much as possible like a random function while still being deterministic and efficiently computable.
A cryptographic hash function is considered insecure if either of the following is computationally feasible:
- finding a (previously unseen) message that matches a given digest
- finding "collisions", wherein two different messages have the same message digest.
An attacker who can do either of these things might, for example, use them to substitute an unauthorized message for an authorized one.
Ideally, it should not even be feasible to find two messages whose digests are substantially similar; nor would one want an attacker to be able to learn anything useful about a message given only its digest besides the digest itself.
Related algorithms
Checksums and cyclic redundancy checks (CRCs) are quite distinct from cryptographic hash functions, and are used for different applications. If used for security, they are vulnerable to attack; for example, a CRC was used for message integrity in the WEP encryption standard, but an attack was readily discovered which exploited the linearity of the checksum specified.
A message authentication code or MAC takes a message and a secret key and generates a "MAC tag", such that it is difficult for an attacker to generate a valid pair(message, tag) that doesn't match one they've already seen; they are used to prevent attackers forging messages, among other uses. Though it is sometimes referred to as a "keyed hash function", a MAC serves a very different purpose and has very different security properties than a cryptographic hash function; for example, it is not considered a flaw if it is easy for someone who knows the MAC key to generate two messages that have the same MAC. Hash functions can be used to create MAC functions; see for example HMAC.
Cryptographic properties
There is no formal definition which captures all of the properties considered desirable for a cryptographic hash function. These properties below are generally considered prerequisites:
- Preimage resistant (See one way for a related but slightly different property): given h it should be hard to find any m such that h = hash(m).
- Second preimage resistant: given an input m1, it should be hard to find another input, m2 (not equal to m1) such that hash(m1) = hash(m2).
- Collision-resistant: it should be hard to find two different messages m1 and m2 such that hash(m1) = hash(m2). Due to a possible birthday attack, this means the hash function output must be at least twice as large as what is required for preimage-resistance.
A hash function meeting these criteria may still have undesirable properties. For instance, most popular hash functions are vulnerable to length-extension attacks: given h(m) and len(m) but not m, by choosing a suitable m' an attacker can calculate h(m || m'), where || denotes concatenation. This property can be used to break naive authentication schemes based on hash functions. The HMAC construction works around these problems.
An ideal hash function would be maximally "boring": it would have no interesting properties such as length extension, and the only interesting way it would differ from a random function would be in that it was deterministic and efficiently computable. This criterion is of course deeply resistant to formal expression; the closest thing to formal expression is the random oracle model, which is an idealization no real hash function can satisfy.
Applications of hash functions
A typical use of a cryptographic hash would be as follows: Alice poses to Bob a tough math problem and claims she has solved it. Bob would like to try it himself, but would yet like to be sure that Alice is not bluffing. Therefore, Alice writes down her solution, appends a random nonce, computes its hash and tells Bob the hash value (whilst keeping the solution secret). This way, when Bob comes up with the solution himself a few days later, Alice can verify his solution but still be able to prove that she had the solution earlier.
In actual practice, Alice and Bob will often be computer programs, and the secret would be something less easily spoofed than a claimed puzzle solution. The above application is called a commitment scheme. Another important application of secure hashes is verification of message integrity. Determination of whether or not any changes have been made to a message (or a file), for example, can be accomplished by comparing message digests calculated before, and after, transmission (or any other event) (for example, see Tripwire , a system using this property as a defense against malware and malfeasance). A message digest can also serve as a means of reliably identifying a file. A related application is password verification. Passwords are usually not stored in clear text, for obvious reasons, but instead in digest form. To authenticate a user, the password presented by the user is hashed and compared with the stored hash.
For both security and performance reasons, most digital signature algorithms specify that only the digest of the message be "signed", not the entire message. Hash functions can also be used in the generation of pseudorandom bits.
SHA-1, MD5, and RIPEMD-160 are among the most commonly-used message digest algorithms as of 2005. In August 2004, researchers found weaknesses in a number of hash functions, including MD5, SHA-0 and RIPEMD. This has called into question the long-term security of later algorithms which are derived from these hash functions — in particular, SHA-1 (a strengthened version of SHA-0), RIPEMD-128, and RIPEMD-160 (both strengthened versions of RIPEMD). Neither SHA-0 nor RIPEMD are widely used since they were replaced by their strengthened versions. In February 2005, an attack on SHA-1 was reported, finding collisions in about 269 hashing operations, rather than the 280 expected for a 160-bit hash function. In August 2005, another attack on SHA-1 was reported, finding collisions in 263 operations.
Hashes are used to identify files on peer-to-peer filesharing networks. For example, in an ed2k link the hash is combined with the file size, providing sufficient information for locating file sources, downloading the file and verifying its contents. [[Magnet: URI scheme|Magnet links]] are another example. Such file hashes are often the top hash of a hash list or a hash tree which allows for additional benefits.
Merkle-Damgård hash functions
- Main article: Merkle-Damgård construction
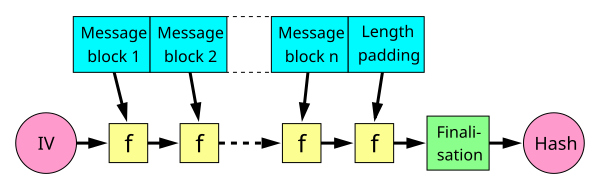
A hash function must be able to process an arbitrary-length message into a fixed-length output. This can be achieved by breaking the input up into a series of equal-sized blocks, and operating on them in sequence using a compression function. The compression function can either be specially designed for hashing or be built from a block cipher. A hash function build with the Merkle-Damgård is as resistant to collisions as is its compression function; any collision for the full hash function can be traced back to a collision in the compression function.
The last block processed should also be unambiguously length padded; this is crucial to the security of this construction. This construction is called the Merkle-Damgård construction. Most widely used hash functions, including SHA-1 and MD5, take this form.
Hash functions based on block ciphers
- Main article: Hash functions based on block ciphers
There are several methods to use a block cipher to build a cryptographic hash function. The methods resemble the block cipher modes of operation usually used for encryption.
Using a block cipher as a hash function is usually much slower than using a specially designed hash function. But, in some cases it is easier because a single implementation of a block cipher can be used for both block cipher and a hash function. It can also save code space in very tiny embedded systems like for instance smart cards or nodes in cars or other machines.
Hash functions to build other cryptographic primitives
Hash functions can be used to build other cryptographic primitives. For these other primitives to be cryptographically secure care has to be taken to build them the right way.
Message authentication codes (MACs) are often built from hash functions. HMAC is such a MAC.
Just as block ciphers can be used to build hash functions, hash functions can be used to build block ciphers. Examples of such block ciphers are SHACAL, BEAR and LION.
Pseudorandom number generators (PRNGs) can be built using hash functions. This is done by combining a (secret) random seed with a counter and hashing it. If the counter is a bignum (allowed to count to any size) then the PRNG can have an infinite period.
Stream ciphers can be built using hash functions. Often this is done by first building a cryptographically secure pseudorandom number generator and then using its stream of random bytes as keystream and XOR that onto the cleartext to get the ciphertext. SEAL is such a stream cipher which is based on SHA-1.
List of cryptographic hash functions
Some of the following algorithms are known to be insecure; consult the article for each specific algorithm for more information on the status of each algorithm. For even more hash functions see the box at the bottom of the page.
| Algorithm | Output size | Internal state size | Block size | Length size | Word size | Collision |
|---|---|---|---|---|---|---|
| HAVAL | 256/224/192/160/128 | 256 | 1024 | 64 | 32 | Yes |
| MD2 | 128 | 384 | 128 | No | 8 | Almost |
| MD4 | 128 | 128 | 512 | 64 | 32 | Yes |
| MD5 | 128 | 128 | 512 | 64 | 32 | Yes |
| PANAMA | 256 | 8736 | 256 | No | 32 | With flaws |
| RIPEMD | 128 | 128 | 512 | 64 | 32 | Yes |
| RIPEMD-128/256 | 128/256 | 128/256 | 512 | 64 | 32 | No |
| RIPEMD-160/320 | 160/320 | 160/320 | 512 | 64 | 32 | No |
| SHA-0 | 160 | 160 | 512 | 64 | 32 | Yes |
| SHA-1 | 160 | 160 | 512 | 64 | 32 | With flaws |
| SHA-256/224 | 256/224 | 256 | 512 | 64 | 32 | No |
| SHA-512/384 | 512/384 | 512 | 1024 | 128 | 64 | No |
| Tiger(2)-192/160/128 | 192/160/128 | 192 | 512 | 64 | 64 | No |
| VEST-4/8 (hash mode) | 160/256 | 176/304 | 8 | 80 | 1 | No |
| VEST-16/32 (hash mode) | 320/512 | 424/680 | 8 | 88 | 1 | No |
| WHIRLPOOL | 512 | 512 | 512 | 256 | 8 | No |
The SHA hash functions are a series of functions developed by the NSA: SHA, also known as SHA-0, SHA-1 and four flavours of a function known as SHA-2.
Note: The internal state here means the "internal hash sum" after each compression of a data block. Most hash algorithms also internally use some additional variables such as length of the data compressed so far since that is needed for the length padding in the end. See the Merkle-Damgård construction for details.
Methods to make hashes of block ciphers
See hash functions based on block ciphers for details.
- Matyas-Meyer-Oseas
- Davies-Meyer
- Miyaguchi-Preneel
- MDC-2
- MDC-4
See also
- Avalanche effect
- MD5CRK
- Message authentication code
- Keyed-hash message authentication code
- CRHF Collision Resistant Hash Functions.
- UOWHF Universal One Way Hash Fuctions.
- CRYPTREC and NESSIE (projects which recommend hash functions)
- Hash list
- Hash tree
External links
- The Hash function lounge — a list of hash functions and known attacks
- Helger Lipmaa's links on hash functions
- Diagrams explaining cryptographic hash functions
- An Illustrated Guide to Cryptographic Hashes by Steve Friedl
- Cryptanalysis of MD5 and SHA: Time for a New Standard by Bruce Schneier
- Hash collision Q&A
- Attacking hash functions by poisoned messages (construction of multiple sensible Postscript messages with the same hash function)