In probability theory and statistics , the chi distribution is a continuous probability distribution . It is the distribution of the square root of the sum of squares of independent random variables having a standard normal distribution , or equivalently, the distribution of the Euclidean distance of the random variables from the origin. The most familiar examples are the Rayleigh distribution with chi distribution with 2 degrees of freedom, and the Maxwell distribution of (normalized) molecular speeds which is a chi distribution with 3 degrees of freedom (one for each spatial coordinate). If
X
i
{\displaystyle X_{i}}
k independent, normally distributed random variables with means
μ
i
{\displaystyle \mu _{i}}
standard deviations
σ
i
{\displaystyle \sigma _{i}}
Y
=
∑
i
=
1
k
(
X
i
−
μ
i
σ
i
)
2
{\displaystyle Y={\sqrt {\sum _{i=1}^{k}\left({\frac {X_{i}-\mu _{i}}{\sigma _{i}}}\right)^{2}}}}
is distributed according to the chi distribution. Accordingly, dividing by the mean of the chi distribution (scaled by the square root of n − 1) yields the correction factor in the unbiased estimation of the standard deviation of the normal distribution . The chi distribution has one parameter:
k
{\displaystyle k}
degrees of freedom (i.e. the number of
X
i
{\displaystyle X_{i}}
Characterization
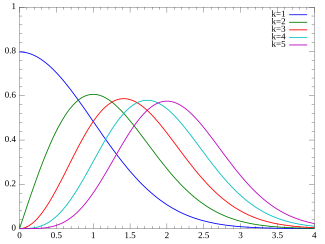
Probability density function
The probability density function (pdf) of the chi-distribution is
f
(
x
;
k
)
=
{
x
k
−
1
e
−
x
2
2
2
k
2
−
1
Γ
(
k
2
)
,
x
≥
0
;
0
,
otherwise
.
{\displaystyle f(x;k)={\begin{cases}{\dfrac {x^{k-1}e^{-{\frac {x^{2}}{2}}}}{2^{{\frac {k}{2}}-1}\Gamma \left({\frac {k}{2}}\right)}},&x\geq 0;\\0,&{\text{otherwise}}.\end{cases}}}
where
Γ
(
z
)
{\displaystyle \Gamma (z)}
gamma function .
Cumulative distribution function
The cumulative distribution function is given by:
F
(
x
;
k
)
=
P
(
k
/
2
,
x
2
/
2
)
{\displaystyle F(x;k)=P(k/2,x^{2}/2)\,}
where
P
(
k
,
x
)
{\displaystyle P(k,x)}
regularized gamma function .
Generating functions
Moment-generating function
The moment-generating function is given by:
M
(
t
)
=
M
(
k
2
,
1
2
,
t
2
2
)
+
{\displaystyle M(t)=M\left({\frac {k}{2}},{\frac {1}{2}},{\frac {t^{2}}{2}}\right)+}
t
2
Γ
(
(
k
+
1
)
/
2
)
Γ
(
k
/
2
)
M
(
k
+
1
2
,
3
2
,
t
2
2
)
{\displaystyle t{\sqrt {2}}\,{\frac {\Gamma ((k+1)/2)}{\Gamma (k/2)}}M\left({\frac {k+1}{2}},{\frac {3}{2}},{\frac {t^{2}}{2}}\right)}
where
M
(
a
,
b
,
z
)
{\displaystyle M(a,b,z)}
confluent hypergeometric function .
Characteristic function
The characteristic function is given by:
φ
(
t
;
k
)
=
M
(
k
2
,
1
2
,
−
t
2
2
)
+
{\displaystyle \varphi (t;k)=M\left({\frac {k}{2}},{\frac {1}{2}},{\frac {-t^{2}}{2}}\right)+}
i
t
2
Γ
(
(
k
+
1
)
/
2
)
Γ
(
k
/
2
)
M
(
k
+
1
2
,
3
2
,
−
t
2
2
)
{\displaystyle it{\sqrt {2}}\,{\frac {\Gamma ((k+1)/2)}{\Gamma (k/2)}}M\left({\frac {k+1}{2}},{\frac {3}{2}},{\frac {-t^{2}}{2}}\right)}
where again,
M
(
a
,
b
,
z
)
{\displaystyle M(a,b,z)}
confluent hypergeometric function .
Properties
Moments
The raw moments are then given by:
μ
j
=
2
j
/
2
Γ
(
(
k
+
j
)
/
2
)
Γ
(
k
/
2
)
{\displaystyle \mu _{j}=2^{j/2}{\frac {\Gamma ((k+j)/2)}{\Gamma (k/2)}}}
where
Γ
(
z
)
{\displaystyle \Gamma (z)}
gamma function . The first few raw moments are:
μ
1
=
2
Γ
(
(
k
+
1
)
/
2
)
Γ
(
k
/
2
)
{\displaystyle \mu _{1}={\sqrt {2}}\,\,{\frac {\Gamma ((k\!+\!1)/2)}{\Gamma (k/2)}}}
μ
2
=
k
{\displaystyle \mu _{2}=k\,}
μ
3
=
2
2
Γ
(
(
k
+
3
)
/
2
)
Γ
(
k
/
2
)
=
(
k
+
1
)
μ
1
{\displaystyle \mu _{3}=2{\sqrt {2}}\,\,{\frac {\Gamma ((k\!+\!3)/2)}{\Gamma (k/2)}}=(k+1)\mu _{1}}
μ
4
=
(
k
)
(
k
+
2
)
{\displaystyle \mu _{4}=(k)(k+2)\,}
μ
5
=
4
2
Γ
(
(
k
+
5
)
/
2
)
Γ
(
k
/
2
)
=
(
k
+
1
)
(
k
+
3
)
μ
1
{\displaystyle \mu _{5}=4{\sqrt {2}}\,\,{\frac {\Gamma ((k\!+\!5)/2)}{\Gamma (k/2)}}=(k+1)(k+3)\mu _{1}}
μ
6
=
(
k
)
(
k
+
2
)
(
k
+
4
)
{\displaystyle \mu _{6}=(k)(k+2)(k+4)\,}
where the rightmost expressions are derived using the recurrence relationship for the gamma function:
Γ
(
x
+
1
)
=
x
Γ
(
x
)
{\displaystyle \Gamma (x+1)=x\Gamma (x)\,}
From these expressions we may derive the following relationships:
Mean:
μ
=
2
Γ
(
(
k
+
1
)
/
2
)
Γ
(
k
/
2
)
{\displaystyle \mu ={\sqrt {2}}\,\,{\frac {\Gamma ((k+1)/2)}{\Gamma (k/2)}}}
Variance:
σ
2
=
k
−
μ
2
{\displaystyle \sigma ^{2}=k-\mu ^{2}\,}
Skewness:
γ
1
=
μ
σ
3
(
1
−
2
σ
2
)
{\displaystyle \gamma _{1}={\frac {\mu }{\sigma ^{3}}}\,(1-2\sigma ^{2})}
Kurtosis excess:
γ
2
=
2
σ
2
(
1
−
μ
σ
γ
1
−
σ
2
)
{\displaystyle \gamma _{2}={\frac {2}{\sigma ^{2}}}(1-\mu \sigma \gamma _{1}-\sigma ^{2})}
Entropy
The entropy is given by:
S
=
ln
(
Γ
(
k
/
2
)
)
+
1
2
(
k
−
ln
(
2
)
−
(
k
−
1
)
ψ
0
(
k
/
2
)
)
{\displaystyle S=\ln(\Gamma (k/2))+{\frac {1}{2}}(k\!-\!\ln(2)\!-\!(k\!-\!1)\psi _{0}(k/2))}
where
ψ
0
(
z
)
{\displaystyle \psi _{0}(z)}
polygamma function .
If
X
∼
χ
k
(
x
)
{\displaystyle X\sim \chi _{k}(x)}
X
2
∼
χ
k
2
{\displaystyle X^{2}\sim \chi _{k}^{2}}
chi-squared distribution )
lim
k
→
∞
χ
k
(
x
)
−
μ
k
σ
k
→
d
N
(
0
,
1
)
{\displaystyle \lim _{k\to \infty }{\tfrac {\chi _{k}(x)-\mu _{k}}{\sigma _{k}}}{\xrightarrow {d}}\ N(0,1)\,}
Normal distribution )If
X
∼
N
(
0
,
1
)
{\displaystyle X\sim N(0,1)\,}
|
X
|
∼
χ
1
(
x
)
{\displaystyle |X|\sim \chi _{1}(x)\,}
If
X
∼
χ
1
(
x
)
{\displaystyle X\sim \chi _{1}(x)\,}
σ
X
∼
H
N
(
σ
)
{\displaystyle \sigma X\sim HN(\sigma )\,}
half-normal distribution ) for any
σ
>
0
{\displaystyle \sigma >0\,}
χ
2
(
x
)
∼
R
a
y
l
e
i
g
h
(
1
)
{\displaystyle \chi _{2}(x)\sim \mathrm {Rayleigh} (1)\,}
Rayleigh distribution )
χ
3
(
x
)
∼
M
a
x
w
e
l
l
(
1
)
{\displaystyle \chi _{3}(x)\sim \mathrm {Maxwell} (1)\,}
Maxwell distribution )
‖
N
i
=
1
,
…
,
k
(
0
,
1
)
‖
2
∼
χ
k
(
x
)
{\displaystyle \|{\boldsymbol {N}}_{i=1,\ldots ,k}{(0,1)}\|_{2}\sim \chi _{k}(x)}
2-norm of
k
{\displaystyle k}
k
{\displaystyle k}
degrees of freedom )chi distribution is a special case of the generalized gamma distribution or the Nakagami distribution or the noncentral chi distribution
Various chi and chi-squared distributions
Name
Statistic
chi-squared distribution
∑
i
=
1
k
(
X
i
−
μ
i
σ
i
)
2
{\displaystyle \sum _{i=1}^{k}\left({\frac {X_{i}-\mu _{i}}{\sigma _{i}}}\right)^{2}}
noncentral chi-squared distribution
∑
i
=
1
k
(
X
i
σ
i
)
2
{\displaystyle \sum _{i=1}^{k}\left({\frac {X_{i}}{\sigma _{i}}}\right)^{2}}
chi distribution
∑
i
=
1
k
(
X
i
−
μ
i
σ
i
)
2
{\displaystyle {\sqrt {\sum _{i=1}^{k}\left({\frac {X_{i}-\mu _{i}}{\sigma _{i}}}\right)^{2}}}}
noncentral chi distribution
∑
i
=
1
k
(
X
i
σ
i
)
2
{\displaystyle {\sqrt {\sum _{i=1}^{k}\left({\frac {X_{i}}{\sigma _{i}}}\right)^{2}}}}
See also
External links
Discrete
with finite with infinite
Continuous
supported on a supported on a supported with support
Mixed
Multivariate Directional Degenerate singular Families