Wikipedia:Reference desk/Science
of the Wikipedia reference desk.
Main page: Help searching Wikipedia
How can I get my question answered?
- Select the section of the desk that best fits the general topic of your question (see the navigation column to the right).
- Post your question to only one section, providing a short header that gives the topic of your question.
- Type '~~~~' (that is, four tilde characters) at the end – this signs and dates your contribution so we know who wrote what and when.
- Don't post personal contact information – it will be removed. Any answers will be provided here.
- Please be as specific as possible, and include all relevant context – the usefulness of answers may depend on the context.
- Note:
- We don't answer (and may remove) questions that require medical diagnosis or legal advice.
- We don't answer requests for opinions, predictions or debate.
- We don't do your homework for you, though we'll help you past the stuck point.
- We don't conduct original research or provide a free source of ideas, but we'll help you find information you need.
How do I answer a question?
Main page: Wikipedia:Reference desk/Guidelines
- The best answers address the question directly, and back up facts with wikilinks and links to sources. Do not edit others' comments and do not give any medical or legal advice.
November 19
COVID-19 numbers in Turkey
Is there somewhere an unbiased estimate of the COVID-19 numbers in Turkey independent of official numbers that Turkish government gives? The stories I hear from hospital doctors and nurses make me scared. Thank you. Hevesli (talk) 17:20, 19 November 2020 (UTC)
- I would never say these resources are "unbiased," but they reflect the views of the United States:
- Alerts and Messages from the US Embassy in Ankara - links and information updated November 18, 2020.
- Travel Advisory for U.S. Citizens.
- The US Embassy publishes their opinions on the COVID-19 situation in Turkey (and elsewhere). I could not find "alternative" published numbers on cases or infection rates except for a link to official sources of the Turkish government; but there is an American interpretation of the situation, which can be summarized as serious, but below the level of the worst emergency conditions. There is not, at this time, a travel restriction nor even a "do not travel" advisory. That doesn't mean it's good: it just means we've seen worse situations in recent history.
- Though in many respects our government is very broken right now, and our State Department has its deficiencies, I can truthfully say that the very first warning I received in late 2019 was from the fine civil servants in the STEP Advisory program who sent a travel advisory about this virus long, long, long before it was a political issue or even catching the top headlines at major news networks. American citizens and other American nationals can sign up for STEP notices at STEP via the Department of State. The opinions expressed through that program are meant to keep traveling Americans safe, and do not necessarily coincide with the official policy statements and political messaging of the rest of the Department or government at large.
- Nimur (talk) 03:40, 20 November 2020 (UTC)
Neutralising bleach
Is there a safe chemical for neutralising bleach for adding to the last rinse for making sure clothings will not be damaged by remaining bleach? Thank you. Hevesli (talk) 17:22, 19 November 2020 (UTC)
- Bleach is an oxidizing agent, so to neutralize it you would need a reducing agent. Most advice I see here recommends sodium metabisulfite, as well as several commercial products designed for the purpose. --Jayron32 19:03, 19 November 2020 (UTC)
- One well known manufacturer of bleach recommends hydrogen peroxide for a neutralising rinse. [1] However they also suggest simply rinsing is generally enough, and you only normally need such a rinse if you need to quickly stop further bleaching, such as when your using bleach for some sort of decorative effect. Nil Einne (talk) 19:28, 19 November 2020 (UTC)
- Interesting question. My wife does any occasional bleaching in a separate bin, hand-washing. I wonder, would running a washer for a full cycle, with no laundry in it, serve to wash away all or most of any bleach residue? ←Baseball Bugs What's up, Doc? carrots→ 23:53, 19 November 2020 (UTC)
- Most household Bleach#Chlorine-based_bleaches are only a 3—6% solution of sodium hypochlorite and excess is easily removed simply by further dilution with water. A full wash cycle would not be needed, simply a brief rinse. Mike Turnbull (talk) 12:00, 20 November 2020 (UTC)
- Aha, so running the washer in "second rinse" mode, for example, should be enough to take care of it. ←Baseball Bugs What's up, Doc? carrots→ 12:33, 20 November 2020 (UTC)
- I don't even bother with an extra rinse. The residual bleach stops any mold/smells from developing. 41.165.67.114 (talk) 12:51, 20 November 2020 (UTC)
- Sure. But what about the OP's original question? If the residual bleach neutralizes molds and smalls, what impact might it have on laundry? ←Baseball Bugs What's up, Doc? carrots→ 13:01, 20 November 2020 (UTC)
- When I started living on my own, I had no washing machine and could not spare the money to go to a launderette. I also did not have a centrifuge or wringer, and not enough space in my 100 square foot attic room to properly hang out the laundry to dry. So on wet days it stayed damp for a relatively long time, long enough that any bleach remnants, while preventing mould from developing, could easily have damaged the fabric. --Lambiam 17:33, 20 November 2020 (UTC)
- Sure. But what about the OP's original question? If the residual bleach neutralizes molds and smalls, what impact might it have on laundry? ←Baseball Bugs What's up, Doc? carrots→ 13:01, 20 November 2020 (UTC)
- I don't even bother with an extra rinse. The residual bleach stops any mold/smells from developing. 41.165.67.114 (talk) 12:51, 20 November 2020 (UTC)
- Aha, so running the washer in "second rinse" mode, for example, should be enough to take care of it. ←Baseball Bugs What's up, Doc? carrots→ 12:33, 20 November 2020 (UTC)
- Most household Bleach#Chlorine-based_bleaches are only a 3—6% solution of sodium hypochlorite and excess is easily removed simply by further dilution with water. A full wash cycle would not be needed, simply a brief rinse. Mike Turnbull (talk) 12:00, 20 November 2020 (UTC)
- Interesting question. My wife does any occasional bleaching in a separate bin, hand-washing. I wonder, would running a washer for a full cycle, with no laundry in it, serve to wash away all or most of any bleach residue? ←Baseball Bugs What's up, Doc? carrots→ 23:53, 19 November 2020 (UTC)
- One well known manufacturer of bleach recommends hydrogen peroxide for a neutralising rinse. [1] However they also suggest simply rinsing is generally enough, and you only normally need such a rinse if you need to quickly stop further bleaching, such as when your using bleach for some sort of decorative effect. Nil Einne (talk) 19:28, 19 November 2020 (UTC)
November 20
perfect glass

I've read that theoretically, if we made a glass which its crystal was perfect we get a much harder material. My question: it will be breakable ( by domestic usage, such as falling glass?). What other properties will be different from regular glass?--Exx8 (talk) 14:51, 20 November 2020 (UTC)
- It is unclear what you mean by "perfect crystal" of glass. Glass is amorphous (non-crystalline) by nature. So anyone who is saying "perfect crystal of glass" is basically speaking bullshit and doesn't know what they are saying. There are crystalline forms of silicon dioxide (the chemical compound that makes up glass); this is called Quartz, and is fairly hard (7 on the Mohs scale) on its own. It's also fantastically common, one of the most common minerals on earth. It's not particularly rare or magical or hard to obtain. If you've been to a beach, most of the sand you are walking on is quartz. --Jayron32 14:57, 20 November 2020 (UTC)
- Common glass is 70-74% quartz soda-lime glass though, soda to make the quartz melt at glassblowing temperatures instead of much higher, the third compound to keep glass from dissolving when it touches water or saliva. And soda-lime glass says there's also aluminum and magnesium oxides and other additives in the mix. Common glass Mohs number (scratchability only, diamonds have been broken by hammers that can't even scratch glass) is quartzy so maybe the monocrystalline version of common glass is as mundane as quartz crystal in fragility but that's not guaranteed without unmelting some glass slowly enough to make crystals the size of common glass objects and grinding or cutting the crystal into a window or cup say and comparing fragilities. Has this been modelled by computer? Sagittarian Milky Way (talk) 18:06, 20 November 2020 (UTC)
- I added a good image to explain the scientific jargon at hand here, which the OP probably ignores.
- The question might also come from a confusion with "crystal glass", a misleading common term for (non-crystalline!) lead glass (or similar modern, non-leaded products imitating its properties). TigraanClick here to contact me
- I refer to the state described here with the enormous tensile strength:
https://en.wikipedia.org/wiki/Strength_of_glass--Exx8 (talk) 15:29, 20 November 2020 (UTC)
- There's nothing there. I assume you're referring to Strength of glass. It's proper URL would be https://en.wikipedia.org/wiki/Strength_of_glass Your -- thingie ran into the URL. ←Baseball Bugs What's up, Doc? carrots→ 15:54, 20 November 2020 (UTC)
- The imperfections that so drastically reduce the tensile strength are not imperfections in a (non-existent) crystal lattice, but mainly minute cracks, typically on the surface, that may be invisible to the eye. When a layer of glass bends under a force, these cracks quickly grow deeper and longer on the side of the surface that is stretched by the bending. (But what is this thing of a glass fibre being strong due to having "have less surface area than regular glass"? What does that mean? For a cylindrical fibre of radius r, the surface-to-volume ratio is 2/r. For a flat sheet of glass whose thickness equals d, that ratio is 2/d. Typically, d >> r, the former being measured in millmetres and the second in microns, so regular glass has a much lower surface-to-volume ratio.) --Lambiam 17:05, 20 November 2020 (UTC)
- so will a perfect glass be unbreakable?--Exx8 (talk) 17:08, 20 November 2020 (UTC)
- No, nothing is unbreakable. Even without any of the above-mentioned surface imperfections, glass is still fairly brittle, meaning with sufficient force of any kind, it will still break. There are ways to make glass more or less strong, so there is an optimum production technique to make it as strong as it could be, but "unbreakable" is not a thing. --Jayron32 17:50, 20 November 2020 (UTC)
- A science teacher told me that about anything would be much harder to break with your hands or Superman's hands if you had to break every chemical bond without help from imperfections down to the size of atoms or molecules. If by perfect one means every atom perfect then nothing is perfect and singling out just glass for this magical property would be misleading. Sagittarian Milky Way (talk) 18:38, 20 November 2020 (UTC)
- Your science teacher seems to have been unaware of the full range of Superman's powers and abilities. ←Baseball Bugs What's up, Doc? carrots→ 22:03, 21 November 2020 (UTC)
- I'm sure Supes could tell the atomically flawless copy is harder to break than the real one even though for him is like toothpick. He can use elevator buttons and poke jail bars like wet noodle with the same finger right, good muscle memory range is a required secondary superpower. Sagittarian Milky Way (talk) 23:49, 21 November 2020 (UTC)
- Your science teacher seems to have been unaware of the full range of Superman's powers and abilities. ←Baseball Bugs What's up, Doc? carrots→ 22:03, 21 November 2020 (UTC)
- A science teacher told me that about anything would be much harder to break with your hands or Superman's hands if you had to break every chemical bond without help from imperfections down to the size of atoms or molecules. If by perfect one means every atom perfect then nothing is perfect and singling out just glass for this magical property would be misleading. Sagittarian Milky Way (talk) 18:38, 20 November 2020 (UTC)
- No, nothing is unbreakable. Even without any of the above-mentioned surface imperfections, glass is still fairly brittle, meaning with sufficient force of any kind, it will still break. There are ways to make glass more or less strong, so there is an optimum production technique to make it as strong as it could be, but "unbreakable" is not a thing. --Jayron32 17:50, 20 November 2020 (UTC)
- so will a perfect glass be unbreakable?--Exx8 (talk) 17:08, 20 November 2020 (UTC)
- Quartz glass, btw, is an actual thing that we make for various uses. For example, a quartz cuvette is necessary for many forms of UV/Vis absorption spectroscopy. Traditional, amorphous glass blocks the passage of UV light, so if you are interested in measuring UV absorption of a sample (for example, if you are examining a protein containing sample where the aromatic amino acid residues absorb in the UV), then you can't use a plastic or a traditional glass cuvette. You need a cuvette made out of quartz. These are expensive, but not rare. For circular dichroism measurement (usually used on proteins), quartz cuvettes are near ubiquitous. Quartz cuvettes and microscope slides are also better to use when performing Raman spectroscopy. You do feel way worse if you break one, though, than if you break a glass cuvette. Each quartz cuvette can run you over $100, while a glass cuvette is probably a few cents. --OuroborosCobra (talk) 20:34, 20 November 2020 (UTC)
- I'm talking about unbreakable for domestic usage. Like throwing a glass onto the wall or the floor...--Exx8 (talk) 20:48, 20 November 2020 (UTC)
- The article Tempered glass explains how glass is strengthened. A tradeoff is that tempered glass cannot be drilled or ground because it will shatter into chunks however this is safer that the jagged shards of ordinary broken glass. PYREX is the brand name of a glass formulation that has low thermal expansion, suitable for cookware. 84.209.119.241 (talk) 00:22, 21 November 2020 (UTC)
- I'm talking about unbreakable for domestic usage. Like throwing a glass onto the wall or the floor...--Exx8 (talk) 20:48, 20 November 2020 (UTC)
November 21
Why are there some cases where one's blood type, semen type, and saliva type don't match?
Apparently in Soviet serial killer Andrei Chikatilo's case, his blood and saliva were of type A whereas his semen was of type AB. What exactly causes such mismatches to occur? Also, were there any other famous cases of such mismatches? Futurist110 (talk) 05:03, 21 November 2020 (UTC)
- I'm not sure this is well studied. Various sources like [2] [3] claim it's because he was non-secretor. But this explanation seems to need major work. As I understand it, for a normal non-secretor, this would mean you can't reliably detect the A or B (or other) antigens in his non-blood bodily fluids (and I mean as antigens, not via DNA testing). I could perhaps imagine a partial
ofor weak secretor may for some reason have reliable detection of either A or B in his other bodily fluids, while not the other. In other words, if you were to say someone is reliably A or B in their semen and saliva, and AB in blood type, this could probably be explained by secretor status. Although if you are only testing a few times it seems also possibly you would just detect A or B by random chance but not the other, which would again explain A or B in their semen and saliva and AB in blood type. I guess on that note, you could perhaps by chance detect one or both in saliva or semen but none or one in semen or saliva. So perhaps you would get A or B in semen or saliva and AB in blood type + saliva or semen. (I find it harder to imagine that you would get this reliably i.e. if you test enough over time it's a persistent result unless there is a condition resulting in red blood cells being persistently present in the semen or saliva, which would seem to be something you would detect anyway.) Anyway the problem is how being a non-secretor explains someone having A (or B) blood and AB saliva or semen. That specific case seems far harder to explain from secretory status from my understanding. Nil Einne (talk) 06:30, 21 November 2020 (UTC) 12:43, 21 November 2020 (UTC) - This may be due to somatic mosaicism, caused by a mutation occurring during mitosis in the developing embryo, particularly in the early blastula stage. Moreover, though very rare, some people are natural chimeras, having developed from the merger, in their mother's womb, of two (or possibly more) fertilized eggs or blastulae. In either case, the cells producing the blood cells and those producing the semen may then have different genotypes. --Lambiam 09:02, 21 November 2020 (UTC)
- Chimerism could also explain genetic differences between tissues in the same person. 167.95.98.207 (talk) 14:28, 23 November 2020 (UTC)
- Isn't that what I said in my second sentence? --Lambiam 12:11, 26 November 2020 (UTC)
What animal has the toughest/most resilient bones, and what animal has the toughest/most resilient flesh? (not shells or coverings, actual meat.
For a Reddit debate. Thanks in advance. --Squeeps10 Talk to meplease ping me 06:05, 21 November 2020 (UTC)
- Strongest bones/skeleton would be found in the large burrowing animals. Wombats, badgers, etc have an interlocking skeletal structure (I guess that's to protect them in case of a cave-in) Their skeletons can easily take the weight of a human standing on their back. 49.182.12.60 (talk) 20:52, 22 November 2020 (UTC)
- I was hoping more for most durable individual bones (IE if I removed a bone, how resistant that bone would be to breaking), not skeletal structures. But thanks for the response.
{{u|Squeeps10}} {Talk}Please ping when replying. 23:23, 22 November 2020 (UTC)
- I was hoping more for most durable individual bones (IE if I removed a bone, how resistant that bone would be to breaking), not skeletal structures. But thanks for the response.
Finite vs. Infinite Universe
First: my highest level of education is high school, so there are almost certainly things I've never thought of with regard to this question that are nevertheless so obvious to most that I'll end up seeming really dumb just for asking. But I had this sort of thought experiment that I wanted to run by some real people
I was thinking about whether or not the universe can physically be infinite in size. So, let's say the universe were a very large, but finite, two dimensional grid of one-foot by one-foot squares. (Let's say it's 100 total squares ... which, come to think of it, actually isn't that large, but whatever.) Now suppose we have some object (an apple, let's say) sitting on one of the squares. We can definitively say that the apple is on the square that it's on, but we can also say that the probability of the apple being on any given square is 1/100, or 1%.
Ok ... now expand the grid so it has infinitely many squares. (Not just a huge number, but literally an infinite number.) We're still looking at the apple, right? But now, isn't the probability of the apple actually being on that square exactly 0? It's just a limit, right? If x is the number of squares, 1/x is the probability of the apple being on a given square. So, as x approaches infinity, the probability approaches 0. Like I said, I'm certain there's a flaw in my thinking. I'm just wondering what it is. Thanks! TheRiseOfSkittlez (talk) 16:44, 21 November 2020 (UTC)
- The natural density of prime numbers per counting number is exactly 0 but infinitely many primes exist. Sagittarian Milky Way (talk) 17:25, 21 November 2020 (UTC)
- Counting on my fingers I find that I have 40% density of prime fingers. Is this not natural? 84.209.119.241 (talk) 01:19, 22 November 2020 (UTC)
- The math(s) with infinity is a bit complex. 1/∞ can be zero or it can be infinitesimal. If it were exactly 0, the universe would be devoid of apples. If it were infinitesimal, there would be an infinite number of apples, spread - infinitly sparsely - on an infinitly larger infinity of squares.
- I recommend poking your nose into Rudy Ruckers thin treatise on this sort of math(s). Reading a page may be quick, considering the concepts thereof takes a while. --Cookatoo.ergo.ZooM (talk) 17:37, 21 November 2020 (UTC)
- In math, there is no such thing as 1/∞. ←Baseball Bugs What's up, Doc? carrots→ 17:52, 21 November 2020 (UTC)
- @BB: As you are a person who refuses to grasp the decimal system, your pontification may be fallible. If memory serves me right, you have also argued on this desk that infinity does not exist. --Cookatoo.ergo.ZooM (talk) 19:28, 21 November 2020 (UTC)
- No, I've argued what my old math teachers told me: Infinity is not a number, it's a concept of boundless expansion. Hence, 1 divided by infinity is mathematic nonsense. ←Baseball Bugs What's up, Doc? carrots→ 21:37, 21 November 2020 (UTC)
- Yeah, so this is the sort of thing that high-school math teachers are indeed wont to say. As with lots of things, depending on what you mean, it can be true, false, or a lie to children.
- High-school math teachers, I think, mostly want to keep their students from plopping ∞ in as a value for variables, and then applying rules that don't work in that case. For example, it's true (in almost any context where it's meaningful) that 1+∞ = 2+∞, but you can't "cancel the infinities" to get 1=2.
- It's also possible that they've internalized a philosophical view that held sway for millennia, from Archimedes through Aquinas to Gauss, that only potential infinity is meaningful. This view began to crumble in the mid-19th century, and arguably was dealt its death blow by Georg Cantor, though it has modern proponents.
- In any case, there are important mathematical contexts in which it is meaningful and true to write 1/∞ = 0. Probably the most salient one is the Riemann sphere, which admittedly has little to do with the question posed by the OP. --Trovatore (talk) 23:02, 21 November 2020 (UTC)
- The limit statement below is the right way to express it. There is no such thing as 1 divided by infinity, because infinity is not a number. But it is valid to say that the "limit" of 1 / n, as n "approaches infinity" (i.e. gets larger and larger) is 0. It just can't ever get to 0. But it can get as close as you want it to, by using ever larger values of n. ←Baseball Bugs What's up, Doc? carrots→ 23:19, 21 November 2020 (UTC)
- Bugs, did you follow the link I posted? While argument from authority is a fallacy, it is also true that I am a mathematician and you are not, so while that certainly doesn't prove I'm right, it might at least be enough cause to follow the link and see what it says. --Trovatore (talk) 23:31, 21 November 2020 (UTC)
- The limit statement below is the right way to express it. There is no such thing as 1 divided by infinity, because infinity is not a number. But it is valid to say that the "limit" of 1 / n, as n "approaches infinity" (i.e. gets larger and larger) is 0. It just can't ever get to 0. But it can get as close as you want it to, by using ever larger values of n. ←Baseball Bugs What's up, Doc? carrots→ 23:19, 21 November 2020 (UTC)
- No, I've argued what my old math teachers told me: Infinity is not a number, it's a concept of boundless expansion. Hence, 1 divided by infinity is mathematic nonsense. ←Baseball Bugs What's up, Doc? carrots→ 21:37, 21 November 2020 (UTC)
- @BB: As you are a person who refuses to grasp the decimal system, your pontification may be fallible. If memory serves me right, you have also argued on this desk that infinity does not exist. --Cookatoo.ergo.ZooM (talk) 19:28, 21 November 2020 (UTC)
- In math, there is no such thing as 1/∞. ←Baseball Bugs What's up, Doc? carrots→ 17:52, 21 November 2020 (UTC)
- Estimated values: 0.9 probability that BB comprehends math including the decimal system, with residual uncertainty about the superiority of the metric system. This minor personal defect reflects a lack of revolutionary zeal. 1.0 probability that Trovatore is a mathematician. The OP may or may not thank him for citing the Riemann sphere as a way to extend a flat universe to infinity in every direction, always handy to know. 0.9 probability that BB followed the link to potential infinity and if so,1.0 probability that BB saw that it says ".. potential infinity is often formalized using the concept of limit." which is prezactly what he has done. 84.209.119.241 (talk) 01:12, 22 November 2020 (UTC)
- To swear by what old maths teachers told one certainly indicates a willingness to accept dicta by authority, possibly bolstered by senescence. But ordinal arithmetic, older than the oldest maths teachers alive, calculates with infinities; rather than infinity being just a number, it reckons with an infinitude of infinite ordinal numbers. --Lambiam 09:04, 22 November 2020 (UTC)
- Estimated values: 0.9 probability that BB comprehends math including the decimal system, with residual uncertainty about the superiority of the metric system. This minor personal defect reflects a lack of revolutionary zeal. 1.0 probability that Trovatore is a mathematician. The OP may or may not thank him for citing the Riemann sphere as a way to extend a flat universe to infinity in every direction, always handy to know. 0.9 probability that BB followed the link to potential infinity and if so,1.0 probability that BB saw that it says ".. potential infinity is often formalized using the concept of limit." which is prezactly what he has done. 84.209.119.241 (talk) 01:12, 22 November 2020 (UTC)
The OP actually calculates the mathematical probability of guessing correctly the location of an apple when that is not already known. If a universe is divided into 100 locations then that probability is indeed 1/100 or 1% provided the italicized condition applies. One also assumes preknowledge that there exists exactly one apple. The example universe might be more realistically 3-dimensional if it is sliced into a grid of 100 cubes rather than squares, without changing the calculation. Moving to the second example of a universe with an infinite number of locations (squares or cubes, as you please), the probability calculation is indeed 1/∞ = 0. There is no contradiction or paradox here and the math holds
Lim x -> ∞ ( 1/x ) = 0.
Consternation arises if one tries to apply probability calculation to something that is already known. If the apple is reliably observed at a location then the probability of it existing there is exactly 1 = certain. The size of the universe has no effect on that calculated certainty unless there is some unspecified uncertainty in making the observation. See articles Probability for a general discussion and Probability theory for a rigorous mathematical treatment. 84.209.119.241 (talk) 19:34, 21 November 2020 (UTC)
The original calculation is missing an assumption, namely that the apple is equally likely to be on any square. That's apparently an application of the principle of indifference, which is not really a universally valid thing.
But I think the more fundamental confusion here is that people (not just the OP) seem to believe uncritically that if something has probability zero, then it can't happen. That's a fallacy unfortunately propagated in most elementary expositions of probability theory, because it's true in a lot of simple situations. But in general, it's just flat false. See almost surely for more details. --Trovatore (talk) 20:01, 21 November 2020 (UTC)
- Almost surely a random point of an infinite universe is not in me. Sagittarian Milky Way (talk) 20:17, 21 November 2020 (UTC)
- Well, there's a nuance there. It's not entirely clear that "a random point of an infinite universe" is meaningful. You can't, for example, put a translation-invariant probability measure on R3, and actually it's for reasons related to the OP's question.
- R3 (usual Euclidean 3-space) can be partitioned into a countably infinite collection of cubical blocks, and the probability of being in any of them should be the same. But if that probability is 0, then because probability measures are countably additive, the probability of being anywhere in the universe would also be 0, which is a contradiction. However, if the probability is anything greater than 0, then the probability of being anywhere in the universe would be ∞, which doesn't make sense either.
However, you can put a finitely additive probability measure on R3,hmm — see below and for some purposes that may be enough. --Trovatore (talk) 21:20, 21 November 2020 (UTC)- I should be careful here. You can't put a translation-invariant finitely additive probability measure that measures all subsets of R3, as shown by the Banach–Tarski paradox. What I had in mind was something like the limiting density of the intersection of the subset with a ball, as the size of the ball goes to infinity (the analogue of what Saggitarian Milky Way was calling "natural density"). That's a fapm, but there are even some pretty simple sets on which it's not well-defined. --Trovatore (talk) 19:59, 23 November 2020 (UTC)
- So the OP is correct in having the intuition that, using maths speak, you can't have a uniform probability distribution over an infinite universe such as Rn (or, for that matter, Zn) for n > 0. However, it does not follow that the universe is finite, even if it is uniform. But an exercise in which one must put a single apple in an absolutely random spot in a universe of infinite extent is unsolvable. Whatever procedure you follow, some spots will be more likely than others. In contrast, there is no mathematical argument against the possibility of putting an infinite number of apples on the squares (large enough to contain an apple) of an infinite checkers board, such that the probability of any square being occupied is a given positive value p (say 1 in 10100, in any case not exceeding 1), but that revealing the occupancy status (yes or no) of any set of squares provides no new information about the status likelihoods of any other square. --Lambiam 23:52, 21 November 2020 (UTC)
- Almost surely a random point of an infinite universe is not in me. Sagittarian Milky Way (talk) 20:17, 21 November 2020 (UTC)
- @TheRiseOfSkittlez: Relevant here is Olbers' paradox. It is a calculation that explains why, with our current observations, it is very unlikely for the universe to be infinitely large because that would mean that, if stars are distributed evenly throughout it, the sky would be infinitely bright (contrary to how it actually looks, being mostly dark). RedPanda25 02:54, 22 November 2020 (UTC)
- That paradox assumes that the universe is infinitely large and infinitely old. It really doesn't apply anymore, now that the Big Bang is considered well-established. --Trovatore (talk) 02:58, 22 November 2020 (UTC)
- Olbers' paradox also assumes that the universe is not expanding. --Lambiam 08:43, 22 November 2020 (UTC)
- That paradox assumes that the universe is infinitely large and infinitely old. It really doesn't apply anymore, now that the Big Bang is considered well-established. --Trovatore (talk) 02:58, 22 November 2020 (UTC)
- A well motivated model of an infinite universe is the eternal inflation model. There are then an infinite number of copies of the exact physical state of the entire observable part of the universe. Quantum mechanics makes the number of possible physical states each finite region of the universe can be in, to be a finite number. Count Iblis (talk) 09:02, 22 November 2020 (UTC)
- Given the existence of one apple and an infinite universe for placement, as well as a uniform probability distribution, then the nonzero infinitesimal probability of it does not imply the existence of any additional apples or an exact zero probability for any position in the universe either, it simply implies, as stated, an infinitesimal probability for each and every position that when taken together always sum to one over the entire universe such that the apple is placed somewhere. Infinitesimals are not real numbers or zeros however, thus, alternatively, these probabilities can be set to zero or almost never. But to express the summation of infinitesimal probabilities: n(1/n)=1 and n=∞ and, importantly, the infinities must have a one-to-one correspondence without which the limit would be indeterminate instead of one as it needs to be. I think that's right, but expect to be persuaded otherwise given prior objections. -Modocc (talk) 18:48, 22 November 2020 (UTC)
- We can entertain a mental construction for picking a random number in the unit interval, given a truly random and fair coin with sides marked "0" and "1", by starting with "0." and creating a binary expansion by appending a (countably) infinite number of flipping outcomes. This will result in some infinite expansion such as "0.1111000010111111110001..." (truncated here to avoid the need of infinite disk space on the Wikimedia servers), or, in decimal notation, "0.940426..." . The probability of hitting exactly this number in this mental model of throwing a dart at the unit interval is, of course, infinitesimally small. For the one-apple infinite universe, however, we do not just need an nonzero infinitesimal probability. We would need a distribution with an everywhere infinitesimal probability density. No mental construction for, to keep it simple, picking a random natural number will give you that. --Lambiam 12:49, 23 November 2020 (UTC)
- No specific random natural number other than 0 can be given, sure, for the others are not large or small enough. Darts, apples or binaries are instances of the exact same mental abstraction since binaries can represent the reals which we use to determine objects' positions in both space and time. For nonzero reals x(1/x) = 1 and I have assumed this particular PDF requires an infinitesimal numbering system for which this works too, but I'm too ill-equipped to either critique or support my assumptions. Individually the limits regarding probability and the sample space size are 0 and ∞, yet when these are taken together their limit has to be 1 when integrating my supposed infinitesimal PDF curve, yet I am not in a position to discern if this is a valid application. -Modocc (talk) 17:35, 23 November 2020 (UTC)
- I am not aware of any successful effort to formulate probability theory in such a way that you can get a uniform probability distribution on a countably infinite set, even by allowing probabilities to be infinitesimal. The first thing you might think of trying would be to use the infinitesimals from nonstandard analysis, but they don't work at all for this purpose. Let me know if you want details. --Trovatore (talk) 19:40, 23 November 2020 (UTC)
- Thanks. I'm not planning on counting infinitesimals and using them, typically because I tend to prefer the more parsimonious solutions. By no "uniform probability distribution on a countably infinite set" I take that to mean one cannot be integrated in the usual fashion if there exists ranges that have zero probability of being selected. However, maybe we just haven't modeled the problem properly yet, for I don't think that's quite true here. One can take a fair coin or die flipped an infinite number of times to select a random permutation from such a set and partition its members (such as odd vs even numbers) in various ways to ensure fairness. And the OP's squares can also be systematically partitioned to test the fairness of the distribution, i.e. given twenty apples how many fall on white squares vs black on an infinite checkered pattern. That an apple is present ex post facto if one is looking at it doesn't diminish the improbability, but in my experience most things are more probable than imagined. -Modocc (talk) 08:06, 24 November 2020 (UTC)
- By flipping a coin say 4 times, giving consecutively 1-0-1-1 (representing oddity vs. evenness) and selecting one half of the remaining numbers, you can restrict N to the subset of numbers whose binary expansion ends on 1101, such as 13, 1975308637, and 1580246913758024691373. So you are down to only a 16th part of the naturals, that is ... precisely as many as you started with. (See also Hilbert's hotel.) It is just not possible to bring the infinite flip sequences into a one-to-one correspondence with the naturals; see Cantor's diagonal argument. After only a finite number of flips, you have not made a dent in whittling down the size of the choice space; at time Aleph-naught you have outflipped it. If a "proper" way of modelling the problem is one that allows some solution of picking (or defining, while remaining logically consistent, a notion of) a "truly random" natural number where no number has better chances than any other, then the reason we just haven't modeled the problem properly yet is that there is just no way of doing that. --Lambiam 15:53, 24 November 2020 (UTC)
- Thanks. I'm not planning on counting infinitesimals and using them, typically because I tend to prefer the more parsimonious solutions. By no "uniform probability distribution on a countably infinite set" I take that to mean one cannot be integrated in the usual fashion if there exists ranges that have zero probability of being selected. However, maybe we just haven't modeled the problem properly yet, for I don't think that's quite true here. One can take a fair coin or die flipped an infinite number of times to select a random permutation from such a set and partition its members (such as odd vs even numbers) in various ways to ensure fairness. And the OP's squares can also be systematically partitioned to test the fairness of the distribution, i.e. given twenty apples how many fall on white squares vs black on an infinite checkered pattern. That an apple is present ex post facto if one is looking at it doesn't diminish the improbability, but in my experience most things are more probable than imagined. -Modocc (talk) 08:06, 24 November 2020 (UTC)
- I am not aware of any successful effort to formulate probability theory in such a way that you can get a uniform probability distribution on a countably infinite set, even by allowing probabilities to be infinitesimal. The first thing you might think of trying would be to use the infinitesimals from nonstandard analysis, but they don't work at all for this purpose. Let me know if you want details. --Trovatore (talk) 19:40, 23 November 2020 (UTC)
- No specific random natural number other than 0 can be given, sure, for the others are not large or small enough. Darts, apples or binaries are instances of the exact same mental abstraction since binaries can represent the reals which we use to determine objects' positions in both space and time. For nonzero reals x(1/x) = 1 and I have assumed this particular PDF requires an infinitesimal numbering system for which this works too, but I'm too ill-equipped to either critique or support my assumptions. Individually the limits regarding probability and the sample space size are 0 and ∞, yet when these are taken together their limit has to be 1 when integrating my supposed infinitesimal PDF curve, yet I am not in a position to discern if this is a valid application. -Modocc (talk) 17:35, 23 November 2020 (UTC)
- We can entertain a mental construction for picking a random number in the unit interval, given a truly random and fair coin with sides marked "0" and "1", by starting with "0." and creating a binary expansion by appending a (countably) infinite number of flipping outcomes. This will result in some infinite expansion such as "0.1111000010111111110001..." (truncated here to avoid the need of infinite disk space on the Wikimedia servers), or, in decimal notation, "0.940426..." . The probability of hitting exactly this number in this mental model of throwing a dart at the unit interval is, of course, infinitesimally small. For the one-apple infinite universe, however, we do not just need an nonzero infinitesimal probability. We would need a distribution with an everywhere infinitesimal probability density. No mental construction for, to keep it simple, picking a random natural number will give you that. --Lambiam 12:49, 23 November 2020 (UTC)
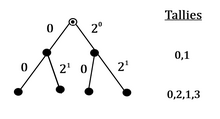
- The sample space size never changes, so if a coin flips only zero, it's unclear to me what is being outflipped. Moreover, if we take the limit of the OP's PDF and we find zero, with an apple no less, as I've noted, the limit of x(1/x) is 1 as it should be. To make my conceptual case clearer, consider an infinite binary tree that begins with the radix point and its edges contain either 0 or a power of 2 that increases with tree depth (see illustration). A self-replicating robot duplicates itself at every node (it initially starts out at the root node with the radix point) with one robot then visiting the node's left child and the other visiting the node's right child, as they each tally the powers of 2 they encounter. Some tallies increase in size others don't, and with an infinite depth every finite nonnegative integer is tallied once by a clone. None have been excluded. Now let the robot start with a cart of apples. Each node is visited by one clone and a fair coin is used to decide which duplicate gets to carry each apple. That way all the clones (thus tallies) have a fair shot of retaining any of the apples whose own total number remains constant throughout, from start to finish. At each level of the tree, the apples' distribution should be uniform and remain so even after the clones complete their infinite summations. Thus we would expect half the apples to land on odd numbers. Now I've done it, I'm at odds with Cantor because I've created a uniform distribution of apples upon an infinite set of clones. Yikes. Maybe we could call it an Apple machine (see Bean machine). Plus we will have to append infinite sets of fraction tallying clones (that traverse trees with negative powers of 2) and dedicate a few bonus apples to the Pi descendant.. -Modocc (talk) 22:49, 24 November 2020 (UTC)
- Given a random finite binary sequence s, however long, the set of natural numbers whose binary expansion ends on s has cardinality . Given a random infinite binary sequence s, with probability 1 it contains infinitely many 1s, and then there exists no natural number whose binary expansion ends on s. That is what I meant by outflipping the space: you go from cardinality to cardinality 0. The tree construction can, in the limit, select with uniform probability a real number in the unit interval – no problem there. It cannot be modified to do the same for selecting a natural number. --Lambiam 12:07, 26 November 2020 (UTC)
- So you are saying we cannot choose from an infinite number of repeated finite numbers embedded in a string. Correct? I agree with that and I should have stated that the army of clones has to march and duplicate in sync to be effective, otherwise we end up talking about n + infinity (which is why I [almost] abandoned this years ago but now I don't see this as a problem either upon seeing how useful the in sync algorithm is here). Note that with the tree their number doubles with their children (see the illustration): there are never duplicates of a number as the tree grows in depth. It is from the tree's infinite leaf nodes, all at the same infinite depth, that has all the unique natural numbers as required. The imaginary bot hoard is just a way to facilitate the distribution of the apples to all of them. I'll add that we can ignore the tree and just exponentially duplicate the bot an infinite number of times with instructions as to what to do with the apples. Of note, if the reals are countable so is Cantor's set T since there is a bijection between them and he set up a strawman. -Modocc (talk) 18:33, 26 November 2020 (UTC)
- Given a random finite binary sequence s, however long, the set of natural numbers whose binary expansion ends on s has cardinality . Given a random infinite binary sequence s, with probability 1 it contains infinitely many 1s, and then there exists no natural number whose binary expansion ends on s. That is what I meant by outflipping the space: you go from cardinality to cardinality 0. The tree construction can, in the limit, select with uniform probability a real number in the unit interval – no problem there. It cannot be modified to do the same for selecting a natural number. --Lambiam 12:07, 26 November 2020 (UTC)
- The sample space size never changes, so if a coin flips only zero, it's unclear to me what is being outflipped. Moreover, if we take the limit of the OP's PDF and we find zero, with an apple no less, as I've noted, the limit of x(1/x) is 1 as it should be. To make my conceptual case clearer, consider an infinite binary tree that begins with the radix point and its edges contain either 0 or a power of 2 that increases with tree depth (see illustration). A self-replicating robot duplicates itself at every node (it initially starts out at the root node with the radix point) with one robot then visiting the node's left child and the other visiting the node's right child, as they each tally the powers of 2 they encounter. Some tallies increase in size others don't, and with an infinite depth every finite nonnegative integer is tallied once by a clone. None have been excluded. Now let the robot start with a cart of apples. Each node is visited by one clone and a fair coin is used to decide which duplicate gets to carry each apple. That way all the clones (thus tallies) have a fair shot of retaining any of the apples whose own total number remains constant throughout, from start to finish. At each level of the tree, the apples' distribution should be uniform and remain so even after the clones complete their infinite summations. Thus we would expect half the apples to land on odd numbers. Now I've done it, I'm at odds with Cantor because I've created a uniform distribution of apples upon an infinite set of clones. Yikes. Maybe we could call it an Apple machine (see Bean machine). Plus we will have to append infinite sets of fraction tallying clones (that traverse trees with negative powers of 2) and dedicate a few bonus apples to the Pi descendant.. -Modocc (talk) 22:49, 24 November 2020 (UTC)
November 23
When less is more in a vaccine
From the recently released preliminary report regarding the Oxford vaccine:
'Prof Andrew Pollard, the trial's lead investigator, [...] protection was 90% in an analysis of around 3,000 people on the trial who were given a half-sized first dose and a full-sized second dose. Prof Pollard said the finding was "intriguing" and would mean "we would have a lot more doses to distribute." '
'Two full doses of the Oxford vaccine gave 62% protection, a half dose followed by a full dose was 90% and overall the trial showed 70% protection.'
according to [| the BBC].
Any plausible explanation for this? Any other vaccine that works like that (lower dose, higher protection)? --Bumptump (talk) 16:56, 23 November 2020 (UTC)
- Sure - most of the realities of the dynamics of biological and physical sciences are well-modeled as nonlinear systems. The defining characteristic - the literal definition - is that the system's response is not proportional to the input.
- So let's flip the question around - why in the world would anybody expect response to be proportional to the amount of dose? Exactly which model of immune response would predict that? When does the dosage linearly relate to treatment efficacy - over a wide range of dosages? I think you will find the answer is "almost never." Nimur (talk) 17:09, 23 November 2020 (UTC)
- That's not entirely fair to the OP, and is attributing to them a question they didn't ask. They never said or implied it should be linearly proportional over a wide range of dosages. They're asking about it being inversely proportional (linearly or non-linearly), over some range. If we flip their question around to "why would we expect response to generally increase with increased dosage over parts of the range", the answer is still "sometimes it doesn't" (and possible reasons for that are given by Mikenorton below). But the question isn't as unreasonable as you make it sound. --Floquenbeam (talk) 17:23, 23 November 2020 (UTC)
- (EC)The BBC story goes on to give two possible explanations: 1. "The immune system rejects the vaccine, which is built around a common cold virus, if it is given too big an initial dose", 2. "The low then high dose may better mimic a coronavirus infection and lead to a better immune response". No comment on the plausibility of these two alternatives. Mikenorton (talk) 17:11, 23 November 2020 (UTC)
- I'll note most vaccines contain adjuvants, not just antigen, which means more moving parts. Biology is complex, and fascinating! Cells and organisms are full of both positive and negative feedback loops. For some reading material: the adaptive immune system has both humoral immunity and cell-mediated immunity "arms", and we want to appropriately twiddle both to get an ideal vaccine response. --47.152.93.24 (talk) 03:09, 24 November 2020 (UTC)
- Plausible explanation: There were just 3 COVID cases in the vaccine group. The probability of having 3 or less if the expectation value was not different from the other group is not all that small (I think the expectation value would be about 7 cases in that group, and then the probability would be about 8%). A fully fledged statistical test would likely increase this probability due to taking into account all sources of statistical fluctuations. Count Iblis (talk) 08:18, 24 November 2020 (UTC)
- I assume by "vaccine group" you mean the group that received first a half dose and then a full dose. The size of that group would be about 3000; a reduction of 101 cases per 10000 to 3 per 3000 would indeed indicate about 90% protection if you do not take a chance element in account. The number 3 is statistically speaking really low; it might as well have turned out to be 4. Based on the data, I don't think you can conclude with any confidence to a protection by the half-then-full regimen that is substantially better than 70%. The best that you can say is that it is likely not to offer less protection than twice full. --Lambiam 15:07, 24 November 2020 (UTC)
- See also Data_dredging#Drawing_conclusions_from_data. The BBC article is a bit thin on info, you can find more facts in this Guardian piece but be cautious. The quotes from researchers give the impression that they are not aware that making hypotheses after you have seen the data is dangerous; maybe the researchers are bad statisticians, or maybe the journalist quoted selectively without realizing the article cut out some important info.
- Notice that even you can compute some sort of statistical threshold to see a "statistically significant" difference between one-shot-and-a-half vs. two-shots, it is still not kosher to deduce it without a follow-up study - some low-probability "pattern" is bound to happen, because there are so many things you could try to see (for instance "bald people are better-protected" or "people whose sum of zipcode digits is a multiple of 7 are better-protected"). (Obligatory XKCD) TigraanClick here to contact me 13:39, 25 November 2020 (UTC)
- Having several experimental groups next to the control group means, for a sanely conducted test, that the researchers also meant to compare the results of the experimental groups. In a two-sided test (the kosher choice), the difference is significant at the 5%-level but not at the 1%-level. Concluding with high confidence (better than 5%-level significance) to a one-sided higher efficacy does require a follow-up. --Lambiam 11:47, 26 November 2020 (UTC)
- The recent announcement that these two groups received different dosages due to an unplanned error means that a comparison between the results of the experimental groups may not have been part of the original plan. This does not invalidate any of my conclusions, including that we cannot conclude that one regimen is substantially better than the other. --Lambiam 16:30, 26 November 2020 (UTC)
November 24
Level of UV required for disinfection
What are the parameters of the UV radiation lamps required to r(d)eactivate certain viruses on surfaces?--86.124.193.84 (talk) 00:59, 24 November 2020 (UTC)
- I'll assume you meant "deactivate", in which case the information on that can be found here.
{{u|Squeeps10}} {Talk}Please ping when replying. 01:01, 24 November 2020 (UTC)- Yes, it was a typo. Can I correct?--86.124.193.84 (talk) 01:05, 24 November 2020 (UTC)
- Certainly, though I see you already have. {{u|Squeeps10}} {Talk} Please ping when replying. 04:34, 24 November 2020 (UTC)
- Yes, it was a typo. Can I correct?--86.124.193.84 (talk) 01:05, 24 November 2020 (UTC)
I see in the mentioned link the "limited published data" statement. How can this data be accessed?--86.124.193.84 (talk) 13:30, 24 November 2020 (UTC)
IRIS, retina biometrics
Will development of cataract and post cataract surgery have any effect on IRIS, Retina biometric details?
https://towardsdatascience.com/biometric-authentication-methods-61c96666883a
- Iris recognition, almost certainly not. Retinal recognition, almost certainly not in the case of cataract surgery, but maybe in cases of retinal detachment with laser re-attachment surgery. Abductive (reasoning) 10:25, 24 November 2020 (UTC)
Using Google Scholar or other resources to determine total body of work
Apologies if this is a stupid question or if I am in the wrong place, but the kind folks at the Teahouse thought the Reference desk might be able to help.
On the article for the engineer Jennie Hwang, it was claimed that she has authored over 600 publications, and I tried to verify this using Google Scholar. To repeat my question on the Talk page:
- Google scholar returns a lot of work where Hwang has contributed, but is there a reliable repository we can use to establish which ones she authored? I feel like adding in the link to the results for her name on Google Scholar is not super helpful as it lists 1,750 results and there's no good way to check for repetition. What sources do we trust to establish research contributions?
Can anyone provide any guidance on this? It seems bizarre that Google is returning over twice the claimed body of work, even with her middle initial in the search. Thank you! A wizard did it (talk) 18:27, 24 November 2020 (UTC)
- I saw your question at the teahouse and did a small piece of investigation, since I use Google scholar often. The problem seems to be that Hwang is a pretty common surname and using initials doesn't really help as there are still too many other authors. The nearest search that I could get to work was "author:Jennie author:Hwang" which gave 169 hits — so 600 seems wrong — but even that list still seems to have some surplus references. There is, for example, a Jennie M. Hwang. If I understand the reason for your search correctly (e.g. to see which of her papers has been often cited) you may be able to manually go through the list and make progress, especially as her own website gives a list of her publications, so you can check the hits were actually by her. It is really difficult to use Google scholar to uniquely get a full author's publication list, unless they have an unusual name. Mike Turnbull (talk) 18:39, 24 November 2020 (UTC)
- If the author has set up their own Google Scholar page, that can be helpful. For example, the late Dr Richard Van Duyne had such a page, and the 637 listed articles are likely all his. --OuroborosCobra (talk) 18:45, 24 November 2020 (UTC)
- Thank you for your answers! so it really has to be manual? That sounds ... painful haha. I'm interested that a list from her own website, or a Google Scholar page curated by the individual might be considered sufficient? I thought you weren't supposed to link to primary sources, but in the interests of improving the article it would be nice to have something to direct readers to that confirms what the article claims, even if it's just from the subject's own website.A wizard did it (talk) 18:55, 24 November 2020 (UTC)
- Isn't this straying into original research? If there isn't a source saying how many articles she wrote, perhaps it shouldn't be in Wikipedia? Alansplodge (talk) 09:04, 25 November 2020 (UTC)
- There is no bar to using primary sources for certain facts. WP:PRIMARY says
A primary source may be used on Wikipedia only to make straightforward, descriptive statements of facts that can be verified by any educated person with access to the primary source
. In the case of an academic, I think that WP:AGF applies to their website for factual data such as a list of publications, which in principle we could verify by checking each claim against the ISBN, DOI or whatever. Hence I believe is reasonable to include in an article such simple statements as "she has authored x books, over y peer-reviewed articles and z patents" with reference to the website — bearing in mind that these figures may get out of date quite quickly. There are now a number of independent, curated, sources of lists of publications for academics, of which the most useful one I have found is "The Academic Family Tree".. This is an interesting source as it allows people to "self-certify" but also allows others to add entries on behalf of third parties. It uses clever software to expand lists of people's publications using their affiliation to institutions and to co-authors and it allows anyone to point out that an attribution is wrong. Sadly, in the case of Dr Hwang, it has no entry (yet!). Incidentally, I think that we can be sure that the current claim in the WP article that she has over 600 publications is clearly nonsense. Mike Turnbull (talk) 13:09, 25 November 2020 (UTC)
- There is no bar to using primary sources for certain facts. WP:PRIMARY says
- Isn't this straying into original research? If there isn't a source saying how many articles she wrote, perhaps it shouldn't be in Wikipedia? Alansplodge (talk) 09:04, 25 November 2020 (UTC)
November 26
Published data re the testing and the required dosage of disinfectants
What published data are there re the testing of various disinfectants like isopropyl alcohol, hydrogen peroxide and lime water and their required dosage and contact time for effectiveness in deactivating the present virus?--86.124.192.169 (talk) 19:00, 26 November 2020 (UTC)
How is the testing done? Are various amounts of virus exposed to various amounts of disinfectants?--86.124.192.169 (talk) 19:04, 26 November 2020 (UTC)
- One of the references in the IPA article from WHO is "Guide to Local Production: WHO-recommended Handrub Formulations" (PDF). World Health Organization. August 2009. which is a pretty good guide to the topic. AFAIK, Covid-19 is no different to other viruses when it comes to the effectiveness of these traditional disinfectants. The "dose" is of course external to the users' body and in normal practice will be a large excess over what is actually required to denature a virus. Mike Turnbull (talk) 10:27, 27 November 2020 (UTC)
November 27
Extant animals with same common and scientific name?
I know the boa constrictor is one example.
Are there any more? 146.200.127.140 (talk) 21:41, 27 November 2020 (UTC)

