Avalanche photodiode

The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.

An avalanche photodiode (APD) is a highly sensitive type of photodiode, which in general are semiconductor diodes that convert light into electricity via interband excitation coupled with impact ionization. APDs use materials and a structure optimised for operating with high reverse bias, approaching the reverse breakdown voltage, such that charge carriers generated by the photoelectric effect are multiplied by an avalanche breakdown; thus they can be used to detect relatively small amounts of light.

From a functional standpoint, they can be regarded as the semiconductor analog of photomultiplier tubes; unlike solar cells, they are not optimised for generating electricity from light but rather for detection of incoming photons. Typical applications for APDs are laser rangefinders, long-range fiber-optic telecommunication, positron emission tomography, and particle physics.

History

The avalanche photodiode was invented by Japanese engineer Jun-ichi Nishizawa in 1952.^[1] However, study of avalanche breakdown, micro-plasma defects in silicon and germanium and the investigation of optical detection using p-n junctions predate this patent.

Principle of operation

Photodiodes generally operate by impact ionization, whereby a photon provides the energy to separate charge carriers in the semiconductor material into a positive and negative pair, which can thus cause a charge flow through the diode. By applying a high reverse bias voltage, any photoelectric effect in the diode can be multiplied by the avalanche effect. Thus, the APD can be thought of as applying a high gain effect to the induced photocurrent.

In general, the higher the reverse voltage, the higher the gain. A standard silicon APD typically can sustain 100–200 V of reverse bias before breakdown, leading to a gain factor of around 100. However, by employing alternative doping and bevelling (structural) techniques compared to traditional APDs, a it is possible to create designs where greater voltage can be applied (> 1500 V) before breakdown is reached, and hence a greater operating gain (> 1000) is achieved.

Among the various expressions for the APD multiplication factor (M), an instructive expression is given by the formula

M={\frac {1}{1-\int _{0}^{L}\alpha (x)\,dx}},

where L is the space-charge boundary for electrons, and $\alpha$ is the multiplication coefficient for electrons (and holes). This coefficient has a strong dependence on the applied electric field strength, temperature, and doping profile. Since APD gain varies strongly with the applied reverse bias and temperature, it is necessary to closely monitor the reverse voltage to keep a stable gain.

Geiger mode counting

If very high gain is needed (10⁵ to 10⁶), detectors related to APDs called SPADs (single-photon avalanche diodes) can be used and operated with a reverse voltage above a typical APD's breakdown voltage. In this case, the photodetector needs to have its signal current limited and quickly diminished. Active and passive current-quenching techniques have been used for this purpose. SPADs that operate in this high-gain regime are sometimes referred to being in Geiger mode. This mode is particularly useful for single-photon detection, provided that the dark count event rate and afterpulsing probability are sufficiently low.

Materials

In principle, any semiconductor material can be used as a multiplication region:

Silicon will detect in the visible and near infrared, with low multiplication noise (excess noise).
Germanium (Ge) will detect infrared out to a wavelength of 1.7 μm, but has high multiplication noise.
InGaAs will detect out to longer than 1.6 μm and has less multiplication noise than Ge. It is normally used as the absorption region of a heterostructure diode, most typically involving InP as a substrate and as a multiplication layer.^[2] This material system is compatible with an absorption window of roughly 0.9–1.7 μm. InGaAs exhibits a high absorption coefficient at the wavelengths appropriate to high-speed telecommunications using optical fibers, so only a few micrometres of InGaAs are required for nearly 100% light absorption.^[2] The excess noise factor is low enough to permit a gain-bandwidth product in excess of 100 GHz for a simple InP/InGaAs system,^[3] and up to 400 GHz for InGaAs on silicon.^[4] Therefore, high-speed operation is possible: commercial devices are available to speeds of at least 10 Gbit/s.^[5]
Gallium-nitride–based diodes have been used for operation with ultraviolet light.
HgCdTe-based diodes operate in the infrared, typically at wavelengths up to about 14 μm, but require cooling to reduce dark currents. Very low excess noise can be achieved in this material system.

Structure

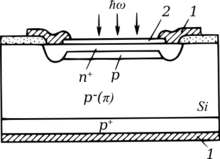
APDs are often not constructed as simple p-n junctions but have more complex designs such as p+-i-p-n+.^[6]

Performance limits

APD applicability and usefulness depends on many parameters. Two of the larger factors are: quantum efficiency, which indicates how well incident optical photons are absorbed and then used to generate primary charge carriers; and total leakage current, which is the sum of the dark current, photocurrent and noise. Electronic dark-noise components are series and parallel noise. Series noise, which is the effect of shot noise, is basically proportional to the APD capacitance, while the parallel noise is associated with the fluctuations of the APD bulk and surface dark currents.

Gain noise, excess noise factor

Another noise source is the excess noise factor, ENF. It is a multiplicative correction applied to the noise that describes the increase in the statistical noise, specifically Poisson noise, due to the multiplication process. The ENF is defined for any device, such as photomultiplier tubes, silicon solid-state photomultipliers, and APDs, that multiplies a signal, and is sometimes referred to as "gain noise". At a gain M, it is denoted by ENF(M) and can often be expressed as

{\text{ENF}}=\kappa M+\left(2-{\frac {1}{M}}\right)(1-\kappa ),

where $\kappa$ is the ratio of the hole impact ionization rate to that of electrons. For an electron multiplication device it is given by the hole impact ionization rate divided by the electron impact ionization rate. It is desirable to have a large asymmetry between these rates to minimize ENF(M), since ENF(M) is one of the main factors that limit, among other things, the best possible energy resolution obtainable.

Conversion noise, Fano factor

The noise term for an APD may also contain a Fano factor, which is a multiplicative correction applied to the Poisson noise associated with the conversion of the energy deposited by a charged particle to the electron-hole pairs, which is the signal before multiplication. The correction factor describes the decrease in the noise, relative to Poisson statistics, due to the uniformity of conversion process and the absence of, or weak coupling to, bath states in the conversion process. In other words, an "ideal" semiconductor would convert the energy of the charged particle into an exact and reproducible number of electron hole pairs to conserve energy; in reality, however, the energy deposited by the charged particle is divided into the generation of electron hole pairs, the generation of sound, the generation of heat, and the generation of damage or displacement. The existence of these other channels introduces a stochastic process, where the amount of energy deposited into any single process varies from event to event, even if the amount of energy deposited is the same.

Further influences

The underlying physics associated with the excess noise factor (gain noise) and the Fano factor (conversion noise) is very different. However, the application of these factors as multiplicative corrections to the expected Poisson noise is similar. In addition to excess noise, there are limits to device performance associated with the capacitance, transit times and avalanche multiplication time.^[2] The capacitance increases with increasing device area and decreasing thickness. The transit times (both electrons and holes) increase with increasing thickness, implying a tradeoff between capacitance and transit time for performance. The avalanche multiplication time times the gain is given to first order by the gain-bandwidth product, which is a function of the device structure and most especially $\kappa \,$ .

References

^ "Jun-ichi Nishizawa – Engineer, Sophia University Special Professor – JAPAN QUALITY REVIEW". Archived from the original on 2018-07-21. Retrieved 2017-05-15.
^ ^a ^b ^c Tsang, W. T., ed. (1985). Semiconductors and Semimetals. Vol. 22, Part D "Photodetectors". Academic Press.
^ Tarof, L. E. (1991). "Planar InP/GaAs Avalanche Photodetector with Gain-Bandwidth Product in Excess of 100 GHz". Electronics Letters. 27 (1): 34–36. Bibcode:1991ElL....27...34T. doi:10.1049/el:19910023.
^ Wu, W.; Hawkins, A. R.; Bowers, J. E. (1997). "Design of InGaAs/Si avalanche photodetectors for 400-GHZ gain-bandwidth product". In Park, Yoon-Soo; Ramaswamy, Ramu V (eds.). Optoelectronic Integrated Circuits. Vol. 3006. pp. 36–47. Bibcode:1997SPIE.3006...38W. doi:10.1117/12.264251. S2CID 109777495. {{cite book}}: |journal= ignored (help)
^ Campbell, J. C. (2007). "Recent advances in Telecommunications Avalanche Photodiodes". Journal of Lightwave Technology. 25 (1): 109–121. Bibcode:2007JLwT...25..109C. doi:10.1109/JLT.2006.888481. S2CID 1398387.
^ "Avalanche Photodiode : Construction, Working & Its Applications". 25 November 2021.