Gradient-domain image processing
Gradient domain image processing, also called Poisson image editing,[1] is a type of digital image processing that operates directly on the differences between neighboring pixels, rather than on the pixel values. Mathematically, an image gradient represents the derivative of an image, so the goal of gradient domain processing is to construct a new image by integrating the gradient, which requires solving Poisson's equation.[2]
Overview
Processing images in the gradient domain is a two-step process. The first step is to choose an image gradient. This is often extracted from one or more images and then modified, but it can also be obtained through other means. For example, some researchers have explored the advantages of users painting directly in the gradient domain,[3] while others have proposed sampling a gradient directly from a camera sensor.[4] The second step is to solve Poisson's equation to find a new image that can produce the gradient from the first step. An exact solution often does not exist because the modified gradient field is no longer conservative, so an image approximating the desired gradient as closely as possible is found.
Image editing
The gradient is obtained from an existing image and modified for image editing purposes. Various operators, such as finite difference or Sobel, can be used to find the gradient of a given image. This gradient can then be manipulated directly to produce several different effects when the resulting image is solved for. For example, if a uniform constant scales the gradient, it results in a simple sharpening filter. A better sharpening filter can be made by only scaling the gradient in areas deemed important.[2] Other uses include seamless image stitching,[5] removal of unwanted details from an image,[1] non-photorealistic rendering filters,[2] image deblocking,[2] the ability to seamlessly clone one part of an image onto another in ways that are difficult to achieve with conventional image-domain techniques,[1] and high-dynamic-range imaging[6] These gradient-domain editing techniques can also be extended to moving images by considering a video clip to be a cube of pixels and solving a 3d Poisson equation.[7]
Seamless image cloning
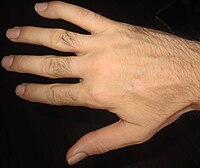
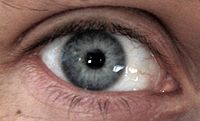
Digital compositing is a common task in image editing in which some or all of one photo is pasted into another. Traditionally, this is done by pasting the pixel values from one image to another. A well-trained artist can make a convincing composite using traditional techniques, but it usually requires time-consuming color correction and mask cutting to make it work. Alternatively, the pasting can be performed in the gradient domain: if the differences between pixels are pasted rather than the actual pixel values, there is sometimes much less user input needed to achieve a clean result. The following example demonstrates the use of gradient-domain image processing to paste from one image to another seamlessly.
-
Input image A
-
Input image B
-
Modified gradient. This is the result of pasting the gradient of B onto the gradient of A.
-
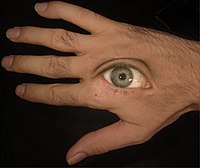
Reconstructed image. This is the result of solving Poisson's equation on the modified gradient. The seam between the two images is barely visible.
-
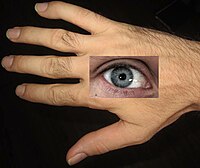
Traditional image domain paste. This is the result of pasting the pixel values directly from B onto A. There is an obvious seam.
Notice that the hand and the eye shifted color slightly in the image reconstructed from the modified gradient. This happened because the solver was set to find the entire image. However, it is possible to add constraints so that only the pasted section is solved, leaving the rest of the image unmodified. It is also worth noting that the gradient pictured above represents the derivative of only one color channel (red) and was rendered with colors representing the strength and direction of the gradient. In practice, two grayscale gradient images are found per color channel, one representing the change in x and the other representing the change in y. Each color channel is solved independently when reconstructing the final image.
References
- ^ a b c Pérez, Patrick; Gangnet, Michel; Blake, Andrew (2003). "Poisson image editing" (PDF). ACM SIGGRAPH 2003 Papers on - SIGGRAPH '03. p. 313. doi:10.1145/1201775.882269. ISBN 1581137095. S2CID 6541990.
- ^ a b c d Bhat, Pravin; Zitnick, C. Lawrence; Cohen, Michael; Curless, Brian (2010). "Gradient Shop" (PDF). ACM Transactions on Graphics. 29 (2): 1–14. doi:10.1145/1731047.1731048. S2CID 3097999.
- ^ McCann, James; Pollard, Nancy S. (2008). "Real-time gradient-domain painting" (PDF). ACM Transactions on Graphics. 27 (3): 1–7. doi:10.1145/1360612.1360692.
- ^ Tumblin, J.; Agrawal, A.; Raskar, R. (2005). "Why I Want a Gradient Camera". 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR'05) (PDF). Vol. 1. pp. 103–110. doi:10.1109/CVPR.2005.374. ISBN 0-7695-2372-2. S2CID 1821571.
- ^ Levin, Anat; Zomet, Assaf; Peleg, Shmuel; Weiss, Yair (2004). "Seamless Image Stitching in the Gradient Domain" (PDF). Computer Vision - ECCV 2004. Lecture Notes in Computer Science. Vol. 3024. pp. 377–389. doi:10.1007/978-3-540-24673-2_31. ISBN 978-3-540-21981-1.
- ^ Fattal, Raanan; Lischinski, Dani; Werman, Michael (2002). "Gradient domain high dynamic range compression" (PDF). Proceedings of the 29th annual conference on Computer graphics and interactive techniques - SIGGRAPH '02. p. 249. doi:10.1145/566570.566573. ISBN 1581135211. S2CID 1650337.
- ^ Wang, Hongcheng; Xu, Ning; Raskar, Ramesh; Ahuja, Narendra (2007). "Videoshop: A new framework for spatio-temporal video editing in gradient domain". Graphical Models. 69: 57–70. doi:10.1016/j.gmod.2006.06.002.