Quantile regression averaging

Quantile Regression Averaging (QRA) is a forecast combination approach to the computation of prediction intervals. It involves applying quantile regression to the point forecasts of a small number of individual forecasting models or experts. It has been introduced in 2014 by Jakub Nowotarski and Rafał Weron and originally used for probabilistic forecasting of electricity prices and loads. Despite its simplicity it has been found to perform extremely well in practice - the top two performing teams in the price track of the Global Energy Forecasting Competition (GEFCom2014) used variants of QRA.

Introduction

The individual point forecasts are used as independent variables and the corresponding observed target variable as the dependent variable in a standard quantile regression setting. The Quantile Regression Averaging method yields an interval forecast of the target variable, but does not use the prediction intervals of the individual methods. One of the reasons for using point forecasts (and not interval forecasts) is their availability. For years, forecasters have focused on obtaining accurate point predictions. Computing probabilistic forecasts, on the other hand, is generally a much more complex task and has not been discussed in the literature nor developed by practitioners so extensively. Therefore, QRA may be found particularly attractive from a practical point of view as it allows to leverage existing development of point forecasting.

Computation

Visualization of the Quantile Regression Averaging (QRA) probabilistic forecasting technique.

The quantile regression problem can be written as follows:

$Q_{y}(q|X_{t})=X_{t}\beta _{q}$,

where $Q_{y}(q|\cdot )$ is the conditional q-th quantile of the dependent variable ($y_{t}$), $X_{t}=[1,{\hat {y}}_{1,t},...,{\hat {y}}_{m,t}]$ is a vector of point forecasts of $m$ individual models (i.e. independent variables) and β_q is a vector of parameters (for quantile q). The parameters are estimated by minimizing the loss function for a particular q-th quantile:

$\min \limits _{\beta _{q}}\left[\sum \limits _{\{t:y_{t}\geq X_{t}\beta _{q}\}}q|y_{t}-X_{t}\beta _{q}|+\sum \limits _{\{t:y_{t}<X_{t}\beta _{q}\}}(1-q)|y_{t}-X_{t}\beta _{q}|\right]=\min \limits _{\beta _{q}}\left[\sum \limits _{t}(q-\mathbf {1} _{y_{t}<X_{t}\beta _{q}})(y_{t}-X_{t}\beta _{q})\right]$

QRA assigns weights to individual forecasting methods and combines them to yield forecasts of chosen quantiles. Although the QRA method is based on quantile regression, not least squares, it still suffers from the same problems: the exogenous variables should not be correlated strongly and the number of variables included in the model has to be relatively small in order for the method to be computationally efficient.

Factor Quantile Regression Averaging (FQRA)

Visualization of the Factor Quantile Regression Averaging (FQRA) probabilistic forecasting technique.

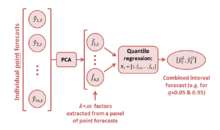
The main difficulty associated with applying QRA comes from the fact that only individual models that perform well and (preferably) are distinct should be used. However, there may be many well performing models or many different specifications of each model (with or without exogenous variables, with all or only selected lags, etc.) and it may not be optimal to include all of them in Quantile Regression Averaging.

In Factor Quantile Regression Averaging (FQRA), instead of selecting individual models a priori, the relevant information contained in all forecasting models at hand is extracted using principal component analysis (PCA). The prediction intervals are then constructed on the basis of the common factors ($f_{t}$) obtained from the panel of point forecasts, as independent variables in a quantile regression. More precisely, in the FQRA method $X_{t}=[1,{\hat {f}}_{1,t},...,{\hat {f}}_{k,t}]$ is a vector of $k<m$ factors extracted from a panel of point forecasts of $m$ individual models, not a vector of point forecasts of the individual models themselves. A similar principal component-type approach was proposed in the context of obtaining point forecasts from the Survey of Professional Forecasters data.

Instead of considering a (large) panel of forecasts of the individual models, FQRA concentrates on a small number of common factors, which - by construction - are orthogonal to each other, and hence are contemporaneously uncorrelated. FQRA can be also interpreted as a forecast averaging approach. The factors estimated within PCA are linear combinations of individual vectors of the panel and FQRA can therefore be used to assign weights to the forecasting models directly.

QRA and LAD regression

QRA may be viewed as an extension of combining point forecasts. The well-known ordinary least squares (OLS) averaging uses linear regression to estimate weights of the point forecasts of individual models. Replacing the quadratic loss function with the absolute loss function leads to quantile regression for the median, or in other words, least absolute deviation (LAD) regression.

See also

• Consensus forecast, also known as combining forecasts, forecast averaging or model averaging (in econometrics and statistics) and committee machines, ensemble averaging or expert aggregation (in machine learning)
• Electricity price forecasting
• Energy forecasting
• Forecasting
• Global Energy Forecasting Competitions
• Economic forecasting
• Prediction interval
• Probabilistic forecasting
• Quantile regression

Implementations

• Matlab code for computing interval forecasts using QRA is available from RePEc: https://ideas.repec.org/c/wuu/hscode/m14003.html