Talk:Arthur Thomas Doodson

Tidal calculations - node factors and equilibrium arguments

Can't see that the calculations take account of node factors and equilibrium arguments. What I really want to know is how you can clauculate node factor and eq arg instead of looking em up in a table. Anyone got ideas? Mister Flash (talk) 18:19, 8 June 2009 (UTC)

After you get the frequencies from the Doodson numbers, you then do a Harmonic Analysis. The equalibrium arguments come out of the harmonic analysis with the amplitudes, and the nodal factors are from the terms fitting Beta_5. Drf5n (talk) 13:50, 18 May 2015 (UTC)

External links modified

Hello fellow Wikipedians,

I have just modified one external link on Arthur Thomas Doodson. Please take a moment to review my edit. If you have any questions, or need the bot to ignore the links, or the page altogether, please visit this simple FaQ for additional information. I made the following changes:

• Added archive https://web.archive.org/web/20100426184722/http://www.pol.ac.uk:80/home/history/doodson.html to http://www.pol.ac.uk/home/history/doodson.html

When you have finished reviewing my changes, please set the checked parameter below to true or failed to let others know (documentation at {{Sourcecheck}}).

This message was posted before February 2018. After February 2018, "External links modified" talk page sections are no longer generated or monitored by InternetArchiveBot. No special action is required regarding these talk page notices, other than regular verification using the archive tool instructions below. Editors have permission to delete these "External links modified" talk page sections if they want to de-clutter talk pages, but see the RfC before doing mass systematic removals. This message is updated dynamically through the template {{source check}} (last update: 5 June 2024).

• If you have discovered URLs which were erroneously considered dead by the bot, you can report them with this tool.
• If you found an error with any archives or the URLs themselves, you can fix them with this tool.

Cheers.—InternetArchiveBot (Report bug) 01:16, 19 October 2016 (UTC)

External links modified

Hello fellow Wikipedians,

I have just modified 3 external links on Arthur Thomas Doodson. Please take a moment to review my edit. If you have any questions, or need the bot to ignore the links, or the page altogether, please visit this simple FaQ for additional information. I made the following changes:

• Added archive https://web.archive.org/web/20090320184406/http://www.pol.ac.uk/home/insight/doodsonmachine.html to http://www.pol.ac.uk/home/insight/doodsonmachine.html
• Added archive https://web.archive.org/web/20110515042248/http://www.pol.ac.uk/home/about.html to http://www.pol.ac.uk/home/about.html
• Added archive https://web.archive.org/web/20110725174153/http://www.airmynyorks.co.uk/20thcent2.htm to http://www.airmynyorks.co.uk/20thcent2.htm

When you have finished reviewing my changes, you may follow the instructions on the template below to fix any issues with the URLs.

This message was posted before February 2018. After February 2018, "External links modified" talk page sections are no longer generated or monitored by InternetArchiveBot. No special action is required regarding these talk page notices, other than regular verification using the archive tool instructions below. Editors have permission to delete these "External links modified" talk page sections if they want to de-clutter talk pages, but see the RfC before doing mass systematic removals. This message is updated dynamically through the template {{source check}} (last update: 5 June 2024).

• If you have discovered URLs which were erroneously considered dead by the bot, you can report them with this tool.
• If you found an error with any archives or the URLs themselves, you can fix them with this tool.

Cheers.—InternetArchiveBot (Report bug) 23:28, 9 July 2017 (UTC)

Usage of Doodson numbers in tidal analysis

[Note: the material below was extracted from the article; it is of very high quality, but not encyclopedic. I'm moving it here, hoping that it can find a new home in Wikibooks perhaps. fgnievinski (talk) 17:46, 27 March 2020 (UTC)]

The usual analysis of a periodic function is in terms of Fourier series, that is, over a period of observation covering a time interval $T$, the behaviour is analysed in terms of sinusoidal cycles having zero, one, two, three, etc. cycles in that period; in other words, a collection of frequencies all being a multiple of a particular fundamental frequency. If for example, measurements are made at $N$ equally-spaced times (thus at times $0$, $h$, $2h$, $3h$, $...$, $(N-1)h=T$) then there are $N$ observations, and the standard analysis provides an amplitude and phase figure for $N/2$ different frequencies having a period of $0$, $T$, $T/2$, $T/3$, etc.

In the case of tidal height (or similarly, tidal current) analysis of the situation is more complex. The frequency (or period) and phase of the forcing cycle is known from astronomical observations, and, there is not just one such frequency. The most important periods are the time of Earth's revolution, the completion of the moon's orbit around the earth, and Earth's orbit around the sun. Notoriously, none of these cycles are convenient multiples of each other. So, rather than proceed with one frequency and its harmonics, multiple frequencies are used.

Further, at each frequency, the influence is not exactly sinusoidal. For each fundamental frequency, the tidal force has the form $A\cos(\omega t+\phi )$ - that is, an amplitude $A$, an angular frequency $\omega$, and a phase $\phi$ related to the choice of a zero time and the orientation of the astronomical attribute at that zero time. However, because the orbits are not circular, the magnitude of the force varies, and this variation is also modeled as a sinusoidal factor (or cosinusoidal), so that the amplitude is given by $A[1+A_{a}\cos(W_{a}t+P_{a})]$ where $A_{a}$ represents the size of the variation around the average value of $A$, $W_{a}$ the angular speed of this variation and $P_{a}$ its phase with regard to the time $t=0$.

Because $\cos(a)\cos(b)=[\cos(a+b)+\cos(a-b)]/2$, a product of cosine terms can be split into the more convenient addition of two simple cosine terms, but having frequencies that are the sum and difference of the frequencies of the two product terms. Thus, where there was one cosine term whose amplitude varied, there are now three terms, with frequencies $\omega$, $\omega +W_{a}$, and $\omega -W_{a}$. Further, although a variation is well represented by a cosine curve, it is not exactly represented by a cosine curve and so each spawns further terms that are multiples of its fundamental frequency just as in the simple Fourier analysis with one fundamental frequency where the variation being analysed is not exactly sinusoidal.

A determined analysis, such as Doodson excelled at, generates not just dozens of terms but hundreds (though many are tiny: tidal prediction might be performed with one or two dozen only) and the Doodson Number is a part of organising the collection. A particular component will be described with a name (M2, S2, etc.) and its angular frequency specified in terms of the Doodson Number, which specified what astronomical frequencies have been added and subtracted for that component. Thus, if $f_{1}$, $f_{2}$, $f_{3}$, $f_{4}$, $f_{5}$, $f_{6}$ are the basic astronomical frequencies, and a particular component has the frequency $(f_{2}+f_{3}-3.f_{5})$, its Doodson Number would be given as 0110-30, meaning $0.f_{1}+1.f_{2}+1.f_{3}+0.f_{4}-3.f_{5}+0.f_{6}$. To avoid the typographical inconvenience of negative signs, the digit string might be presented with five added to each component so that fanciful example would be presented as 566525, except that the first digit may not have five added.

Precise usage depends on the precise choice of the component frequency definitions, whether or not five is added (if not, the string might be called an Indicative Doodson Number), and also, as some forces vary only slowly with time, a calculation once a month (say) might suffice so certain components might not be separated into additive terms following that variation.

Code

This is adapted from a script for the MATLAB system, and its main merit is that it actually does generate a suitable curve. In more general work, times and phases are usually referenced to GMT, and the prediction would be annotated with actual dates and times.

 % Speed in degrees per hour for various Earth-Moon-Sun astronomical attributes, as given in Tides, Surges and Mean Sea-Level, D.T. Pugh.
 clear EMS;
 % T + s - h                         +15            w0: Nominal day, ignoring the variation followed via the Equation of Time.
 EMS.T = +360/(1.0350)/24;          %+14.492054485  w1: is the advance of the moon's longitude, referenced to the Earth's zero longitude, one full rotation in 1.0350 mean solar days.
 EMS.s = +360/(27.3217)/24;         % +0.5490141536 w2: Moon around the earth in 27.3217 mean solar days.
 EMS.h = +360/(365.2422)/24;        % +0.0410686388 w3: Earth orbits the sun in a tropical year of 365.24219879 days, not the 365.2425 in 365 + y/4 - y/100 + y/400. Nor with - y/4000.
 EMS.p = +360/(365.25* 8.85)/24;    % +0.0046404    w4: Precession of the moon's perigee, once in 8.85 Julian years: apsides.
 EMS.N = -360/(365.25*18.61)/24;    % -0.00220676   w5: Precession of the plane of the moon's orbit, once in 18.61 Julian years: negative, so recession.
 EMS.pp= +360/(365.25*20942)/24;    % +0.000001961  w6: Precession of the perihelion, once in 20942 Julian years.
 % T + s = 15.041068639°/h is the rotation of the earth with respect to the fixed stars, as both are in the same sense.

NOTE: This should say T + h = 15.041068639°/h
And it's not with respect to the fixed stars, but with respect to the equinox. (EMS.s should be based on the tropical month, ca 27.3216 days, rather than on the sidereal month, ca 27.3217 days.)
Eric Kvaalen (talk) 13:48, 16 September 2022 (UTC)

 %                   Reference                      Angular Speed           Degrees/hour  Period in Days.  Astronomical Values.
 % Sidereal day      Distant star                   ws = w0 + w3 = w1 + w2  15.041                0.9973
 % Mean solar day    Solar transit of meridian      w0 = w1 + w2 - w3       15                    1
 % Mean lunar day    Lunar transit of meridian      w1                      14.4921               1.0350
 % Month Draconic    Lunar ascending node           w2 + w5                   .5468              27.4320

NOTE: This should be w2 - w5, giving 0.55122091 degrees/hour and a draconic month of 27.2123 days
And thanks to NickyMcLean for inserting this code back in 2007! Eric Kvaalen (talk) 09:41, 22 January 2022 (UTC)

 % Month Sidereal    Distant star                   w2                        .5490              27.3217    27d07h43m11.6s  27.32166204
 % Month Anomalistic Lunar Perigee (apsides)        w2 - w4                   .5444              27.5546
 % Month Synodic     Lunar phase                    w2 - w3 = w0 - w1         .5079              29.5307    29d12h44m02.8s  29.53058796
 % Year Tropical     Solar ascending node           w3                        .0410686          365.2422   365d05h48m45s   365.24218967  at 2000AD. 365.24219879 at 1900AD.
 % Year Sidereal     Distant star                                             .0410670          365.2564   365d06h09m09s   365.256363051 at 2000AD.
 % Year Anomalistic  Solar perigee (apsides)        w3 - w6                   .0410667          365.2596   365d06h13m52s   365.259635864 at 2000AD.
 % Year nominal      Calendar                                                                   365 or 366
 % Year Julian                                                                                  365.25
 % Year Gregorian                                                                               365.2425
 % Obtaining definite values is tricky: years of 365, 365.25, 365.2425 or what days? These parameters also change with time.

 clear Tide;
 %                                          w1 w2 w3 w4 w5 w6
 Tide.Name{1} = 'M2';   Tide.Doodson{ 1} = [+2  0  0  0  0  0]; Tide.Title{ 1} = 'Principal lunar, semidiurnal';
 Tide.Name{2} = 'S2';   Tide.Doodson{ 2} = [+2 +2 -2  0  0  0]; Tide.Title{ 2} = 'Principal solar, semidiurnal';
 Tide.Name{3} = 'N2';   Tide.Doodson{ 3} = [+2 -1  0 +1  0  0]; Tide.Title{ 3} = 'Principal lunar elliptic, semidiurnal';
 Tide.Name{4} = 'L2';   Tide.Doodson{ 4} = [+2 +1  0 -1  0  0]; Tide.Title{ 4} = 'Lunar semi-diurnal: with N2 for varying speed around the ellipse';
 Tide.Name{5} = 'K2';   Tide.Doodson{ 5} = [+2 +2 -1  0  0  0]; Tide.Title{ 5} = 'Sun-Moon angle, semidiurnal';
 Tide.Name{6} = 'K1';   Tide.Doodson{ 6} = [+1 +1  0  0  0  0]; Tide.Title{ 6} = 'Sun-Moon angle, diurnal';
 Tide.Name{7} = 'O1';   Tide.Doodson{ 7} = [+1 -1  0  0  0  0]; Tide.Title{ 7} = 'Principal lunar declinational';
 Tide.Name{8} = 'Sa';   Tide.Doodson{ 8} = [ 0  0 +1  0  0  0]; Tide.Title{ 8} = 'Solar, annual';
 Tide.Name{9} = 'nu2';  Tide.Doodson{ 9} = [+2 -1 +2 -1  0  0]; Tide.Title{ 9} = 'Lunar evectional constituent: pear-shapedness due to the sun';
 Tide.Name{10} = 'Mm';  Tide.Doodson{10} = [ 0 +1  0 -1  0  0]; Tide.Title{10} = 'Lunar evectional constituent: pear-shapedness due to the sun';
 Tide.Name{11} = 'P1';  Tide.Doodson{11} = [+1 +1 -2  0  0  0]; Tide.Title{11} = 'Principal solar declination';
 Tide.Constituents = 11;
 % Because w0 + w3 = w1 + w2, the basis set {w0,...,w6} is not independent. Usage of w0 (or of EMS.T) can be eliminated.
 % For further pleasure w2 - w6 correspond to other's usage of w1 - w5.

 % Collect the basic angular speeds into an array as per A. T. Doodson's organisation. The classic Greek letter omega is represented as w.
 clear w;
 % w(0) = EMS.T + EMS.s - EMS.h;	% This should be w(0), but MATLAB doesn't allow this!
 w(1) = EMS.T;	
 w(2) = EMS.s;
 w(3) = EMS.h;
 w(4) = EMS.p;
 w(5) = EMS.N;
 w(6) = EMS.pp;

 % Prepare the basis frequencies, of sums and differences. Doodson's published coefficients typically have 5 added
 % so that no negative signs will disrupt the layout: the scheme here does not have the offset.
 disp('Name °/hour  Hours   Days');
 for i = 1:Tide.Constituents
  Tide.Speed(i) = sum(Tide.Doodson{i}.*w);    % Sum terms such as DoodsonNumber(j)*w(j) for j = 1:6.
  disp([int2str(i),' ',Tide.Name{i},' ',num2str(Tide.Speed(i)),' ',num2str(360/Tide.Speed(i)),' ',num2str(15/Tide.Speed(i)),' ',Tide.Title{i}]);
 end;

 clear Place;
 % The amplitude H and phase for each constituent are determined from the tidal record by least-squares
 % fitting to the observations of the amplitudes of the astronomical terms with expected frequencies and phases.
 % The number of constituents needed for accurate prediction varies from place to place.
 % In making up the tide tables for Long Island Sound, the National Oceanic and Atmospheric Administration
 % uses 23 constituents. The eleven whose amplitude is greater than .1 foot are:
 Place(1).Name = 'Bridgeport, Cn';	% Counting time in hours from midnight starting Sunday 1 September 1991.
 %                  M2      S2     N2    L2    K2     K1     O1    Sa   nu2    Mm     P1...
 Place(1).A = [  3.185   0.538  0.696 0.277 0.144  0.295  0.212 0.192 0.159 0.108  0.102];	% Tidal heights (feet)
 Place(1).P = [-127.24 -343.66 263.60 -4.72 -2.55 142.02 505.93 301.5 45.70 86.82 340.11];	% Phase (degrees). 
 % The values for these coefficients are taken from http://www.math.sunysb.edu/~tony/tides/harmonic.html
 % which originally came from a table published by the US. National Oceanic and Atmospheric Administration.

 % Calculate a tidal height curve, in terms of hours since the start time.
 PlaceCount = 1;
 Colour=cellstr(strvcat('g','r','b','c','m','y','k'));	% A collection.
 clear y;
 step = 0.125; LastHour = 720; % 8760 hours in a year.
 n = LastHour/step + 1;
 y(1:n,1:PlaceCount) = 0;
 t = (0:step:LastHour)/24;
 for it = 1:PlaceCount
  i = 0;
  for h = 0:step:LastHour
   i = i + 1;
   y(i,it) = sum(Place(it).A.*cosd(Tide.Speed*h + Place(it).P)); %Sum terms A(j)*cos(speed(j)*h + p(j)) for j = 1:Tide.Constituents.
  end;      % Should use cos(ix) = 2*cos([i - 1]*x)*cos(x) - cos([i - 2]*x), but, for clarity...
 end;

 figure(1); clf; hold on; title('Tidal Height'); xlabel('Days');
 for it = 1:PlaceCount
  plot(t,y(1:n,it),Colour{it});
 end;
 legend(Place(1:PlaceCount).Name,'Location','NorthWest');

Results

This shows the common pattern of two tidal peaks in a day, though remember that the repeat time is not exactly twelve hours but 12.4206 hours. The two peaks are not equal: the twin tidal bulges beneath the moon and on the far side of the earth are aligned with the moon. Bridgeport is north of the equator, so when the moon is north of the equator also and shining upon Bridgeport, Bridgeport is closer to its maximum effect than approximately twelve hours later when Bridgeport is on the far side of the earth from the moon and the high tide bulge at Bridgeport's longitude has its maximum south of the equator. Thus the two high tides a day alternate in maximum heights: lower high (just under three feet), higher high (just over three feet), and again. Likewise for the low tides.

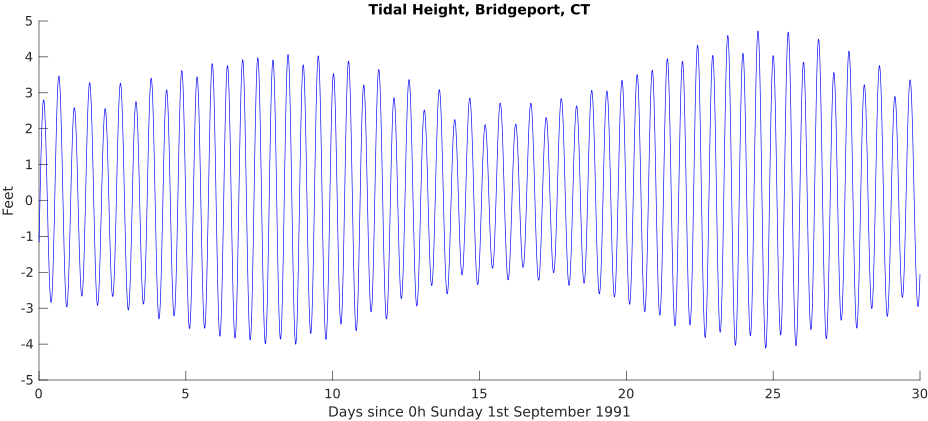
This shows the spring tide/ neap tide cycle in the amplitudes of the tides as the moon orbits the earth from being in line (Sun - Earth - Moon, or Sun - Moon - Earth) when the two main influences combine to give the spring tides, to when the two forces are opposing each other as when the angle Moon - Earth - Sun is close to ninety degrees producing the neap tides. Note also as the moon moves around its orbit it also changes from north of the equator to south of the equator. The alternation in the heights of the high tides becomes smaller, until they are the same (the moon is above the equator), then redevelops but with the other polarity, waxing to a maximum difference and then waning again.

This shows just over a year's worth of tidal height calculations. The sun also cycles between being north or south of the equator and as well the Earth - Sun and Earth - Moon distances change on their own cycles. None of the various cycle periods are commensurate, and the pattern does not repeat.

Remember always that calculated tidal heights take no account of weather effects, nor include any changes to conditions since the coefficients were determined, such as movement of sandbanks or dredging, etc.