Jump to content

User:Tomruen/Convex uniform tetracomb

From Wikipedia, the free encyclopedia
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.

Regular and uniform honeycombs

There are five fundamental affine Coxeter groups that generate regular and uniform tessellations in 4-space.[1]

# Coxeter group Coxeter-Dynkin diagram
1 A~4 [(3,3,3,3,3)] [3[5]]
2 B~4 [4,3,3,4]
3 C~4 [4,3,31,1] h[4,3,3,4]
4 D~4 [31,1,1,1] q[4,3,3,4]
5 F~4 [3,4,3,3] h[4,3,3,4]

There are three regular honeycomb of Euclidean 4-space:

  1. tesseractic honeycomb, with symbols {4,3,3,4}, = . There are 19 uniform honeycombs in this family.
  2. 24-cell honeycomb, with symbols {3,4,3,3}, . There are 31 uniform honeycombs in this family.
  3. 16-cell honeycomb, with symbols {3,3,4,3},

Other families that generate uniform honeycombs:

  • There are 23 uniform honeycombs, 4 unique in the 16-cell honeycomb family. With symbols h{4,32,4} it is geometrically identical to the 16-cell honeycomb, =
  • There are 7 uniform honeycombs from the A~4, family, all unique.
  • There are 9 uniform honeycombs in the D~4: [31,1,1,1] family, all repeated in other families, including the 16-cell honeycomb.

Non-Wythoffian uniform tessellations in 4-space also exist by elongation (inserting layers), and gyration (rotating layers) from these reflective forms.

The single-ringed tessellations are given below, indexed by Olshevsky's listing.

Duoprismatic forms

  • B~2xB~2: [4,4]x[4,4] = [4,3,3,4] = (Same as tesseractic honeycomb family)
  • B~2xH~2: [4,4]x[6,3]
  • H~2xH~2: [6,3]x[6,3]
  • A~2xB~2: [Δ]x[4,4] (Same forms as [6,3]x[4,4])
  • A~2xH~2: [Δ]x[6,3] (Same forms as [6,3]x[6,3])
  • A~2xA~2: [Δ]x[Δ] (Same forms as [6,3]x[6,3])

Prismatic forms

  • B~3xI~1: [4,3,4]x[∞]
  • D~3xI~1: [4,31,1]x[∞]
  • A~3xI~1:

Noncompact prismatic forms

  • A3xI~1: [3,3]x[∞] -
  • B3xI~1: [4,3]x[∞] -
  • H3xI~1: [5,3]x[∞] -
  • I~1xI~1xI2r: [∞] x [∞] x [r] = [4,4]x[r] - =

Non-Wythoffian forms

The non-Wythoffian forms are built as stacked composites of these prismatic noncompact groups:

  • I2pxI~1xA1: [p]x[∞]x[ ] - (Prism column)
  • D~3xA1: [4,31,1]x[ ] (Prism slab)
  • A~3xA1: (Prism slab)
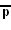
  • A~2xI2p: [Δ]x[p] (Prism slab)
  • B~2xI2p: [4,4]x[p] (Prism slab)
  • H~2xI2p: [6,3]x[p] (Prism slab)


B~4 [4,3,3,4] family

# Coxeter-Dynkin
andSchläfli
symbols 		Name Facets by location: [4,3,3,4]
4 3 2 1 0

[4,3,3]
[4,3]×[ ]
[4]×[4]
[ ]×[3,4]
[3,3,4]
1
t0{4,3,3,4} 		Tesseractic honeycomb {4,3,3}
 - - - -
87
t1{4,3,3,4} 		Rectified tesseractic honeycomb t1{4,3,3}
 - - - {3,3,4}
88
t2{4,3,3,4} 		Birectified tesseractic honeycomb
(Same as 24-cell honeycomb {3,4,3,3}) 		t1{3,3,4}
 - - - t1{3,3,4}
89
t0,1{4,3,3,4} 		Truncated tesseractic honeycomb t0,1{4,3,3} - - - {3,3,4}
90
t0,2{4,3,3,4} 		Cantellated tesseractic honeycomb
(Small prismatotesseractic honeycomb) 		t0,2{4,3,3} - - {}x{3,4} t1{3,3,4}
91
t0,3{4,3,3,4} 		Runcinated tesseractic honeycomb
(Small diprismatotesseractic honeycomb)
92
t1,2{4,3,3,4} 		Bitruncated tesseractic honeycomb
93
t1,3{4,3,3,4} 		Bicantellated tesseractic honeycomb
(Same as Rectified 24-cell honeycomb t1{3,4,3,3})
[1]
t0,4{4,3,3,4} 		Stericated tesseractic honeycomb
(same as tesseractic honeycomb)
94
t0,1,2{4,3,3,4} 		Cantitruncated tesseractic honeycomb
(Great prismatotesseractic honeycomb)
95
t0,1,3{4,3,3,4} 		Runcitruncated tesseractic honeycomb
(Small tomocubic-diprismatotesseractic honeycomb)
96
t0,1,4{4,3,3,4} 		Steritruncated tesseractic honeycomb
(Tomotesseractic-diprismatotesseractic honeycomb)
97
t0,2,3{4,3,3,4} 		Runcicantellated tesseractic honeycomb
(Rhombitesseractic-diprismatotesseractic honeycomb)
98
t0,2,4{4,3,3,4} 		Stericantellated tesseractic honeycomb
(Small rhombitesseractic-prismatotesseractic honeycomb)
99
t1,2,3{4,3,3,4} 		Bicantitruncated tesseractic honeycomb
(Same as Truncated 24-cell honeycomb, t0,1{3,4,3,3} )
100
t0,1,2,3{4,3,3,4} 		Runcicantitruncated tesseractic honeycomb
(Great diprismatotesseractic honeycomb)
101
t0,1,2,4{4,3,3,4} 		Stericantitruncated tesseractic honeycomb
(Great rhombitesseractic-prismatotesseractic honeycomb)
102
t0,1,3,4{4,3,3,4} 		Steriruncitruncated tesseractic honeycomb
(Great tomocubic-diprismatotesseractic honeycomb)
103
t0,1,2,3,4{4,3,3,4} 		Omnitruncated tesseractic honeycomb

C~4 [31,1,3,4] family

There are 23 honeycombs in this family,[2] all listed below.

# Coxeter-Dynkin
andSchläfli
symbols
File:CDel B5 nodes.png 		Name Facets by location: [31,1,3,4]
4 3 2 1 0

[3,3,4]
[31,1,1]
[3,3]×[ ]
[ ]×[3]×[ ]
[3,3,4]
104
{31,1,3,4} 		16-cell honeycomb {3,3,4}
 {31,1,1}
 - - -
105
t0,1{31,1,3,4} 		Truncated 16-cell honeycomb
(Same as truncated 16-cell honeycomb, t0,1{3,3,4,3})
106
t0,2{31,1,3,4} 		Cantellated 16-cell honeycomb
(Same as birectified 16-cell honeycomb)
107
t0,1,2{31,1,3,4} 		Cantitruncated 16-cell honeycomb
(Same as bitruncated 16-cell honeycomb)
108
t0,3{31,1,3,4} 		Runcinated 16-cell honeycomb
(Small diprismatodemitesseractive honeycomb)
109
t0,1,3{31,1,3,4} 		Runcitruncated 16-cell honeycomb
(Small prismato16-cell honeycomb)
110
t0,2,3{31,1,3,4} 		Runcicantellated 16-cell honeycomb
(Great prismato16-cell honeycomb)
111
t0,1,2,3{31,1,3,4} 		Runcicantitruncated 16-cell honeycomb
(Great diprismato16-cell honeycomb)
[88]
t1{31,1,3,4} 		Rectified 16-cell honeycomb
(Same as 24-cell honeycomb, {3,4,3,3})
(Also birectified tesseractic honeycomb) 		t1{3,3,4}
 t1{31,1,1}

 - - t1{3,3,4}
[87]
t2{31,1,3,4} 		Same as rectified tesseractic honeycomb t1{4,3,3}
 {31,1,1}
 - - t1{4,3,3}
[1]
t3{31,1,3,4} 		Same as tesseractic honeycomb {4,3,3}
 - - - {4,3,3}
[87]
t0,4{31,1,3,4} 		(Same as Rectified tesseractive honeycomb)
[92]
t1,2{31,1,3,4} 		(Same as bitruncated tesseractic honeycomb)
[90]
t1,3{31,1,3,4} 		(Same as cantellated tesseractic honeycomb)
[89]
t2,3{31,1,3,4} 		(Same as truncated tesseractic honeycomb)
[92]
t0,1,4{31,1,3,4} 		(Same as bitruncated tesseractic honeycomb)
[93]
t0,2,4{31,1,3,4} 		(Same as rectified 24-cell honeycomb)
(Also bicantellated tesseractic honeycomb)
[91]
t0,3,4{31,1,3,4} 		(Same as runcinated tesseractic honeycomb)
[94]
t1,2,3{31,1,3,4} 		(Same as cantitruncated tesseractic honeycomb)
[99]
t0,1,2,4{31,1,3,4} 		(Same as bicantitruncated tesseractic honeycomb)
[97]
t0,1,3,4{31,1,3,4} 		(Same as runcicantellated tesseractic honeycomb)
[95]
t0,2,3,4{31,1,3,4} 		(Same as runcitruncated tesseractic honeycomb)
[100]
t0,1,2,3,4{31,1,3,4} 		(Same as runcicantitruncated tesseractic honeycomb)

F~4 [3,4,3,3] family

There are 32 honeycombs in this family, 31 reflective forms and one snub.[3] They are named as truncated forms from the regular 16-cell honeycomb and 24-cell honeycomb. These 31 forms are listed by the regular generators in two groups of 19, with 7 shared between.

From the regular 24-cell honeycomb, 19 forms are:

# Coxeter-Dynkin
andSchläfli
symbols 		Name Facets by location: [3,4,3,3]
4 3 2 1 0

[3,4,3]
[3,4]×[ ]
[3]×[3]
[ ]×[3,3]
[4,3,3]
104
{3,4,3,3} 		24-cell honeycomb {3,4,3} - - - -
[93]
t1{3,4,3,3} 		Rectified 24-cell honeycomb t1{3,4,3} - - - {4,3,3}
106
t2{3,4,3,3} 		Birectified 24-cell honeycomb t1{3,4,3} - - - t1{4,3,3}
106
t2{3,4,3,3} 		Birectified 24-cell honeycomb
105
t0,1{3,4,3,3} 		Truncated 24-cell honeycomb
107
t1,2{3,4,3,3} 		Bitruncated 24-cell honeycomb
?
t0,2{3,4,3,3} 		Cantellated 24-cell honeycomb
116
t1,3{3,4,3,3} 		Bicantellated 24-cell honeycomb
122
t0,3{3,4,3,3} 		Runcinated 24-cell honeycomb
121
t0,4{3,4,3,3} 		Stericated 24-cell honeycomb
[99]
t0,1,2{3,4,3,3} 		Cantitruncated 24-cell honeycomb
119
t1,2,3{3,4,3,3} 		Bicantitruncated 24-cell honeycomb
128
t0,1,3{3,4,3,3} 		Runcitruncated 24-cell honeycomb
125
t0,2,3{3,4,3,3} 		Runcicantellated 24-cell honeycomb
127
t0,1,4{3,4,3,3} 		Steritruncated 24-cell honeycomb
124
t0,2,4{3,4,3,3} 		Stericantellated 24-cell honeycomb
131
t0,1,2,3{3,4,3,3} 		Runcicantitruncated 24-cell honeycomb
130
t0,1,2,4{3,4,3,3} 		Stericantitruncated 24-cell honeycomb
129
t0,1,3,4{3,4,3,3} 		Steriruncitruncated 24-cell honeycomb
132
t0,1,2,3,4{3,4,3,3} 		Omnitruncated 24-cell honeycomb
[133]
t0,1,2{3,3,4,3} 		Snub 24-cell honeycomb

From the regular 16-cell honeycomb, 19 forms are:

# Coxeter-Dynkin
andSchläfli
symbols 		Name Facets by location: [3,3,4,3]
4 3 2 1 0

[3,3,4]
[3,3]×[ ]
[3]×[3]
[ ]×[4,3]
[3,4,3]
88
t0{3,3,4,3} 		16-cell honeycomb
[104]
t1{3,3,4,3} 		Rectified 16-cell honeycomb t1{3,3,4} - - - {3,4,3}
[106]
t2{3,3,4,3} 		Birectified 16-cell honeycomb
[99]
t0,1{3,3,4,3} 		Truncated 16-cell honeycomb
113
t1,2{3,3,4,3} 		Bitruncated 16-cell honeycomb
112
t0,2{3,3,4,3} 		Cantellated 16-cell honeycomb
[116]
t1,3{3,3,4,3} 		Bicantellated 16-cell honeycomb
115
t0,3{3,3,4,3} 		Runcinated 16-cell honeycomb
[121]
t0,4{3,3,4,3} 		Stericated 16-cell honeycomb
114
t0,1,2{3,3,4,3} 		Cantitruncated 16-cell honeycomb
[119]
t1,2,3{3,3,4,3} 		Bicantitruncated 16-cell honeycomb
117
t0,1,3{3,3,4,3} 		Runcitruncated 16-cell honeycomb
118
t0,2,3{3,3,4,3} 		Runcicantellated 16-cell honeycomb
123
t0,1,4{3,3,4,3} 		Steritruncated 16-cell honeycomb
[124]
t0,2,4{3,3,4,3} 		Stericantellated 16-cell honeycomb
120
t0,1,2,3{3,3,4,3} 		Runcicantitruncated 16-cell honeycomb
126
t0,1,2,4{3,3,4,3} 		Stericantitruncated 16-cell honeycomb
[129]
t0,1,3,4{3,3,4,3} 		Steriruncitruncated 16-cell honeycomb
[132]
t0,1,2,3,4{3,3,4,3} 		Omnitruncated 16-cell honeycomb
[133]
t0,1{3,4,3,3} 		Snub 24-cell honeycomb

A~4 [3[5]] family

There are 7 honeycombs in this family,[4] all unique to this family, all given below.

# Coxeter-Dynkin
andSchläfli
symbols 		Name Facets by location
4 3 2 1 0

[3,3,3]
[ ]x[3,3]
[3]x[3]
[3,3]x[ ]
[3,3,3]
134
{3[5]} 		5-cell honeycomb
135
t0,1{3[5]} 		Truncated 5-cell honeycomb
136
t0,2{3[5]} 		Cantellated 5-cell honeycomb
137
t0,1,2{3[5]} 		Cantitruncated 5-cell honeycomb
138
t0,1,3{3[5]} 		Runcitruncated 5-cell honeycomb
139
t0,1,2,3{3[5]} 		Runcicantitruncated 5-cell honeycomb
140
t0,1,2,3,4{3[5]} 		Omnitruncated 5-cell honeycomb

D~4 [31,1,1,1] family

There are 9 honeycombs in this family,[5] all repeated, with all 9 forms given below.

# Coxeter-Dynkin
andSchläfli
symbols 		Name Facets by location: [3,4,3,3]
4 3 2 1 0
[?]
{31,1,1,1} 		-
[104]
t4{31,1,1,1} 		Same as 24-cell honeycomb - t1{31,1,1}

 t1{31,1,1}

 t1{31,1,1}

 t1{31,1,1}

[?]
t0,4{31,1,1,1} 		-
[?]
t0,1{31,1,1,1} 		-
[?]
t0,1,4{31,1,1,1} 		-
[?]
t0,1,2{31,1,1,1} 		-
[?]
t0,1,4{31,1,1,1} 		-
[?]
t0,1,2,3{31,1,1,1} 		{}x{}x{}x{}
t0,2,3{31,1,1}

 t0,2,3{31,1,1}

 t0,2,3{31,1,1}

 t0,2,3{31,1,1}

[?]
t0,1,2,3,4{31,1,1,1} 		{}x{}x{}x{}
 t0,1,2,3{31,1,1}

 t0,1,2,3{31,1,1}

 t0,1,2,3{31,1,1}

 t0,1,2,3{31,1,1}

Duoprismatic forms

Coxeter groups:

  • B~2xB~2: [4,4]x[4,4]
  • B~2xH~2: [4,4]x[6,3]
  • H~2xH~2: [6,3]x[6,3]

[4,4]×[4,4]

There are 15 reflective combinatoric forms, but only 3 unique ones.

# Coxeter-Dynkin
andSchläfli
symbols 		Name
1
[1]
6
[1]
[6]
[1]
[6]
[1]
[6]
63
[6]
[63]
[1]
[6]
[63]
10
[10]
67
[10]
[67]

[4,4]x[6,3]

There are 35 reflective combinatoric forms.

# Coxeter-Dynkin Name

[6,3]x[6,3]

There are 28 reflective combinatoric forms.

# Coxeter-Dynkin diagram Name

References

  1. ^ George Olshevsky (2006), Uniform Panoploid Tetracombs, manuscript. Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs.
  2. ^ Olshevsky section V
  3. ^ Olshevsky section VI
  4. ^ Olshevsky section VII
  5. ^ Olshevsky section VII
Retrieved from "https://en.wikipedia.org/enwiki/w/index.php?title=User:Tomruen/Convex_uniform_tetracomb&oldid=571197257"