Jump to content

Maxwell's demon

From Wikipedia, the free encyclopedia
(Redirected from Demon of Maxwell)
Schematic figure of Maxwell's demon thought experiment

Maxwell's demon is a thought experiment that appears to disprove the second law of thermodynamics. It was proposed by the physicist James Clerk Maxwell in 1867.[1] In his first letter, Maxwell referred to the entity as a "finite being" or a "being who can play a game of skill with the molecules". Lord Kelvin would later call it a "demon".[2]

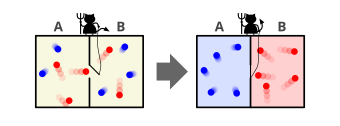
In the thought experiment, a demon controls a door between two chambers containing gas. As individual gas molecules (or atoms) approach the door, the demon quickly opens and closes the door to allow only fast-moving molecules to pass through in one direction, and only slow-moving molecules to pass through in the other. Because the kinetic temperature of a gas depends on the velocities of its constituent molecules, the demon's actions cause one chamber to warm up and the other to cool down. This would decrease the total entropy of the system, seemingly without applying any work, thereby violating the second law of thermodynamics.

The concept of Maxwell's demon has provoked substantial debate in the philosophy of science and theoretical physics, which continues to the present day. It stimulated work on the relationship between thermodynamics and information theory. Most scientists argue that, on theoretical grounds, no practical device can violate the second law in this way. Other researchers have implemented forms of Maxwell's demon in experiments, though they all differ from the thought experiment to some extent and none has been shown to violate the second law.

Origin and history of the idea

[edit]

The thought experiment first appeared in a letter Maxwell wrote to Peter Guthrie Tait on 11 December 1867. It appeared again in a letter to John William Strutt in 1871, before it was presented to the public in Maxwell's 1872 book on thermodynamics titled Theory of Heat.[3]

In his letters and books, Maxwell described the agent opening the door between the chambers as a "finite being". Being a deeply religious man, he never used the word "demon". Instead, William Thomson (Lord Kelvin) was the first to use it for Maxwell's concept, in the journal Nature in 1874, and implied that he intended the Greek mythology interpretation of a daemon, a supernatural being working in the background, rather than a malevolent being.[2][4][5]

Original thought experiment

[edit]

The second law of thermodynamics ensures (through statistical probability) that two bodies of different temperature, when brought into contact with each other and isolated from the rest of the Universe, will evolve to a thermodynamic equilibrium in which both bodies have approximately the same temperature.[6] The second law is also expressed as the assertion that in an isolated system, entropy never decreases.[6]

Maxwell conceived a thought experiment as a way of furthering the understanding of the second law. His description of the experiment is as follows:[6][7]

... if we conceive of a being whose faculties are so sharpened that he can follow every molecule in its course, such a being, whose attributes are as essentially finite as our own, would be able to do what is impossible to us. For we have seen that molecules in a vessel full of air at uniform temperature are moving with velocities by no means uniform, though the mean velocity of any great number of them, arbitrarily selected, is almost exactly uniform. Now let us suppose that such a vessel is divided into two portions, A and B, by a division in which there is a small hole, and that a being, who can see the individual molecules, opens and closes this hole, so as to allow only the swifter molecules to pass from A to B, and only the slower molecules to pass from B to A. He will thus, without expenditure of work, raise the temperature of B and lower that of A, in contradiction to the second law of thermodynamics.

In other words, Maxwell imagines one container divided into two parts, A and B.[6][8] Both parts are filled with the same gas at equal temperatures and placed next to each other. Observing the molecules on both sides, an imaginary demon guards a trapdoor between the two parts. When a faster-than-average molecule from A flies towards the trapdoor, the demon opens it, and the molecule will fly from A to B. Likewise, when a slower-than-average molecule from B flies towards the trapdoor, the demon will let it pass from B to A. The average speed of the molecules in B will have increased while in A they will have slowed down on average. Since average molecular speed corresponds to temperature, the temperature decreases in A and increases in B, contrary to the second law of thermodynamics. A heat engine operating between the thermal reservoirs A and B could extract useful work from this temperature difference.

The demon must allow molecules to pass in both directions in order to produce only a temperature difference; one-way passage only of faster-than-average molecules from A to B will cause higher temperature and pressure to develop on the B side.

Criticism and development

[edit]

Several physicists have presented calculations that show that the second law of thermodynamics will not actually be violated, if a more complete analysis is made of the whole system including the demon.[6][8][9] The essence of the physical argument is to show, by calculation, that any demon must "generate" more entropy segregating the molecules than it could ever eliminate by the method described. That is, it would take more thermodynamic work to gauge the speed of the molecules and selectively allow them to pass through the opening between A and B than the amount of energy gained by the difference of temperature caused by doing so.

One of the most famous responses to this question was suggested in 1929 by Leó Szilárd,[10] and later by Léon Brillouin.[6][8] Szilárd pointed out that a real-life Maxwell's demon would need to have some means of measuring molecular speed, and that the act of acquiring information would require an expenditure of energy. Since the demon and the gas are interacting, we must consider the total entropy of the gas and the demon combined. The expenditure of energy by the demon will cause an increase in the entropy of the demon, which will be larger than the lowering of the entropy of the gas.

In 1960, Rolf Landauer raised an exception to this argument.[6][8][11] He realized that some measuring processes need not increase thermodynamic entropy as long as they were thermodynamically reversible. He suggested these "reversible" measurements could be used to sort the molecules, violating the Second Law. However, due to the connection between entropy in thermodynamics and information theory, this also meant that the recorded measurement must not be erased. In other words, to determine whether to let a molecule through, the demon must acquire information about the state of the molecule and either discard it or store it. Discarding it leads to immediate increase in entropy, but the demon cannot store it indefinitely. In 1982, Charles Bennett showed that, however well prepared, eventually the demon will run out of information storage space and must begin to erase the information it has previously gathered.[8][12] Erasing information is a thermodynamically irreversible process that increases the entropy of a system. Although Bennett had reached the same conclusion as Szilard's 1929 paper, that a Maxwellian demon could not violate the second law because entropy would be created, he had reached it for different reasons. Regarding Landauer's principle, the minimum energy dissipated by deleting information was experimentally measured by Eric Lutz et al. in 2012. Furthermore, Lutz et al. confirmed that in order to approach the Landauer's limit, the system must asymptotically approach zero processing speed.[13] Recently, Landauer's principle has also been invoked to resolve an apparently unrelated paradox of statistical physics, Loschmidt’s paradox. [14]

John Earman and John D. Norton have argued that Szilárd and Landauer's explanations of Maxwell's demon begin by assuming that the second law of thermodynamics cannot be violated by the demon, and derive further properties of the demon from this assumption, including the necessity of consuming energy when erasing information, etc.[15][16] It would therefore be circular to invoke these derived properties to defend the second law from the demonic argument. Bennett later acknowledged the validity of Earman and Norton's argument, while maintaining that Landauer's principle explains the mechanism by which real systems do not violate the second law of thermodynamics.[17]

Recent progress

[edit]

Although the argument by Landauer and Bennett only answers the consistency between the second law of thermodynamics and the whole cyclic process of the entire system of a Szilard engine (a composite system of the engine and the demon), a recent approach based on the non-equilibrium thermodynamics for small fluctuating systems has provided deeper insight on each information process with each subsystem. From this viewpoint, the measurement process is regarded as a process where the correlation (mutual information) between the engine and the demon increases, decreasing the entropy of the system in an amount given by the mutual information.[18] If the correlation changes, thermodynamic relations such as the second law of thermodynamics and the fluctuation theorem for each subsystem should be modified, and for the case of external control a second-law like inequality[18][19][20] and a generalized fluctuation theorem[21] with mutual information are satisfied. For more general information processes including biological information processing, both inequality[22] and equality[23] with mutual information hold. When repeated measurements are performed, the entropy reduction of the system is given by the entropy of the sequence of measurements,[18][24][25] which takes into account the reduction of information due to the correlation between the measurements.

Applications

[edit]

Real-life versions of Maxwellian demons occur, but all such "real demons" or molecular demons have their entropy-lowering effects duly balanced by increase of entropy elsewhere.[26] Molecular-sized mechanisms are no longer found only in biology; they are also the subject of the emerging field of nanotechnology. Single-atom traps used by particle physicists allow an experimenter to control the state of individual quanta in a way similar to Maxwell's demon.

If hypothetical mirror matter exists, Zurab Silagadze proposes that demons can be envisaged, "which can act like perpetuum mobiles of the second kind: extract heat energy from only one reservoir, use it to do work and be isolated from the rest of ordinary world. Yet the Second Law is not violated because the demons pay their entropy cost in the hidden (mirror) sector of the world by emitting mirror photons."[27]

Experimental work

[edit]

In 2007, David Leigh announced the creation of a nano-device based on the Brownian ratchet popularized by Richard Feynman. Leigh's device is able to drive a chemical system out of equilibrium, but it must be powered by an external source (light in this case) and therefore does not violate thermodynamics.[28]

Previously, researchers including Nobel Prize winner Fraser Stoddart had created ring-shaped molecules called rotaxanes which could be placed on an axle connecting two sites, A and B. Particles from either site would bump into the ring and move it from end to end. If a large collection of these devices were placed in a system, half of the devices had the ring at site A and half at B, at any given moment in time.[29]

Leigh made a minor change to the axle so that if a light is shone on the device, the center of the axle will thicken, restricting the motion of the ring. It keeps the ring from moving, however, only if it is at A. Over time, therefore, the rings will be bumped from B to A and get stuck there, creating an imbalance in the system. In his experiments, Leigh was able to take a pot of "billions of these devices" from 50:50 equilibrium to a 70:30 imbalance within a few minutes.[30]

In 2009, Mark G. Raizen developed a laser atomic cooling technique which realizes the process Maxwell envisioned of sorting individual atoms in a gas into different containers based on their energy.[6][31][32] The new concept is a one-way wall for atoms or molecules that allows them to move in one direction, but not go back. The operation of the one-way wall relies on an irreversible atomic and molecular process of absorption of a photon at a specific wavelength, followed by spontaneous emission to a different internal state. The irreversible process is coupled to a conservative force created by magnetic fields and/or light. Raizen and collaborators proposed using the one-way wall in order to reduce the entropy of an ensemble of atoms. In parallel, Gonzalo Muga and Andreas Ruschhaupt independently developed a similar concept. Their "atom diode" was not proposed for cooling, but rather for regulating the flow of atoms. The Raizen Group demonstrated significant cooling of atoms with the one-way wall in a series of experiments in 2008. Subsequently, the operation of a one-way wall for atoms was demonstrated by Daniel Steck and collaborators later in 2008. Their experiment was based on the 2005 scheme for the one-way wall, and was not used for cooling. The cooling method realized by the Raizen Group was called "single-photon cooling", because only one photon on average is required in order to bring an atom to near-rest. This is in contrast to other laser cooling techniques which use the momentum of the photon and require a two-level cycling transition.

In 2006, Raizen, Muga, and Ruschhaupt showed in a theoretical paper that as each atom crosses the one-way wall, it scatters one photon, and information is provided about the turning point and hence the energy of that particle. The entropy increase of the radiation field scattered from a directional laser into a random direction is exactly balanced by the entropy reduction of the atoms as they are trapped by the one-way wall.

This technique is widely described as a "Maxwell's demon" because it realizes Maxwell's process of creating a temperature difference by sorting high and low energy atoms into different containers. However, scientists have pointed out that it does not violate the second law of thermodynamics,[6][33] does not result in a net decrease in entropy,[6][33] and cannot be used to produce useful energy. This is because the process requires more energy from the laser beams than could be produced by the temperature difference generated. The atoms absorb low entropy photons from the laser beam and emit them in a random direction, thus increasing the entropy of the environment.[6][33]

In 2014, Pekola et al. demonstrated an experimental realization of a Szilárd engine.[34][35] Only a year later and based on an earlier theoretical proposal,[36] the same group presented the first experimental realization of an autonomous Maxwell's demon, which extracts microscopic information from a system and reduces its entropy by applying feedback. The demon is based on two capacitively coupled single-electron devices, both integrated on the same electronic circuit. The operation of the demon is directly observed as a temperature drop in the system, with a simultaneous temperature rise in the demon arising from the thermodynamic cost of generating the mutual information.[37] In 2016, Pekola et al. demonstrated a proof-of-principle of an autonomous demon in coupled single-electron circuits, showing a way to cool critical elements in a circuit with information as a fuel.[38] Pekola et al. have also proposed that a simple qubit circuit, e.g., made of a superconducting circuit, could provide a basis to study a quantum Szilard's engine.[39]

As metaphor

[edit]

Daemons in computing, generally processes that run on servers to respond to users, are named for Maxwell's demon.[40]

Historian Henry Brooks Adams, in his manuscript The Rule of Phase Applied to History, attempted to use Maxwell's demon as a historical metaphor, though he misunderstood and misapplied the original principle.[41] Adams interpreted history as a process moving towards "equilibrium", but he saw militaristic nations (he felt Germany pre-eminent in this class) as tending to reverse this process, a Maxwell's demon of history. Adams made many attempts to respond to the criticism of his formulation from his scientific colleagues, but the work remained incomplete at his death in 1918 and was published posthumously.[42]

See also

[edit]

Notes

[edit]
  1. ^ Cargill Gilston Knott (1911). "Quote from undated letter from Maxwell to Tait". Life and Scientific Work of Peter Guthrie Tait. Cambridge University Press. pp. 213–215.
  2. ^ a b Thomson, William (9 April 1874). "Kinetic theory of the dissipation of energy". Nature. 9 (232): 441–444. Bibcode:1874Natur...9..441T. doi:10.1038/009441c0.
  3. ^ Leff & Rex (2002), p. 370.
  4. ^ "The sorting demon of Maxwell". Nature. 20 (501): 126. 1879. Bibcode:1879Natur..20Q.126.. doi:10.1038/020126a0.
  5. ^ Weber, Alan S. (2000). Nineteenth Century Science: a Selection of Original Texts. Broadview Press. p. 300.
  6. ^ a b c d e f g h i j k Bennett, Charles H. (November 1987). "Demons, Engines, and the Second Law" (PDF). Scientific American. 257 (5): 108–116. Bibcode:1987SciAm.257e.108B. doi:10.1038/scientificamerican1187-108. Archived from the original (PDF) on December 3, 2020. Retrieved November 13, 2014.
  7. ^ Maxwell (1871), reprinted in Leff & Rex (1990) on p. 4.
  8. ^ a b c d e Sagawa, Takahiro (2012). Thermodynamics of Information Processing in Small Systems. Springer Science and Business Media. pp. 9–14. ISBN 978-4431541677.
  9. ^ Bennett, Charles H.; Schumacher, Benjamin (August 2011). "Maxwell's demons appear in the lab" (PDF). Nikkei Science: 3–6. Retrieved November 13, 2014.
  10. ^ Szilard, Leo (1929). "Über die Entropieverminderung in einem thermodynamischen System bei Eingriffen intelligenter Wesen (On the reduction of entropy in a thermodynamic system by the intervention of intelligent beings)". Zeitschrift für Physik. 53 (11–12): 840–856. Bibcode:1929ZPhy...53..840S. doi:10.1007/bf01341281. S2CID 122038206. cited in Bennett 1987. English translation available as NASA document TT F-16723 published 1976
  11. ^ Landauer, R. (1961). "Irreversibility and heat generation in the computing process" (PDF). IBM Journal of Research and Development. 5 (3): 183–191. doi:10.1147/rd.53.0183. Retrieved November 13, 2014. reprinted in Vol. 44, No. 1, January 2000, p. 261 Archived 2016-03-03 at the Wayback Machine
  12. ^ Bennett, C. H. (1982). "The thermodynamics of computation—a review" (PDF). International Journal of Theoretical Physics (Submitted manuscript). 21 (12): 905–940. Bibcode:1982IJTP...21..905B. CiteSeerX 10.1.1.655.5610. doi:10.1007/BF02084158. S2CID 17471991. Archived from the original (PDF) on 2014-10-14. Retrieved 2017-12-10.
  13. ^ Ball, Philip (2012). "The unavoidable cost of computation revealed". Nature. doi:10.1038/nature.2012.10186. S2CID 2092541.
  14. ^ Binder, P.M. (2023). "The reversibility paradox: Role of the velocity reversal step". International Journal of Theoretical Physics. 62 (9): 200. Bibcode:2023IJTP...62..200B. doi:10.1007/s10773-023-05458-x.
  15. ^ Earman, John & Norton, John D. (1998). "Exorcist XIV: The Wrath of Maxwell's Demon. Part I. From Maxwell to Szilard" (PDF). Studies in History and Philosophy of Modern Physics. 29 (4): 435. Bibcode:1998SHPMP..29..435E. doi:10.1016/s1355-2198(98)00023-9.
  16. ^ Earman, John & Norton, John D. (1999). "Exorcist XIV: The Wrath of Maxwell's Demon. Part II. From Szilard to Landauer and Beyond" (PDF). Studies in History and Philosophy of Modern Physics. 30 (1): 1. Bibcode:1999SHPMP..30....1E. doi:10.1016/s1355-2198(98)00026-4.
  17. ^ Bennett, Charles H. (2002–2003). "Notes on Landauer's principle, reversible computation, and Maxwell's demon". Studies in History and Philosophy of Modern Physics. 34 (3): 501–510. arXiv:physics/0210005. Bibcode:2003SHPMP..34..501B. doi:10.1016/S1355-2198(03)00039-X. S2CID 9648186.
  18. ^ a b c Cao, F. J.; Feito, M. (2009-04-10). "Thermodynamics of feedback controlled systems". Physical Review E. 79 (4): 041118. arXiv:0805.4824. Bibcode:2009PhRvE..79d1118C. doi:10.1103/PhysRevE.79.041118. ISSN 1539-3755. PMID 19518184.
  19. ^ Sagawa, Takahiro; Ueda, Masahito (2008-02-26). "Second Law of Thermodynamics with Discrete Quantum Feedback Control". Physical Review Letters. 100 (8): 080403. arXiv:0710.0956. Bibcode:2008PhRvL.100h0403S. doi:10.1103/PhysRevLett.100.080403. PMID 18352605. S2CID 41799543.
  20. ^ Hugo Touchette & Seth Lloyd (2000). "Information-Theoretic Limits of Control". Physical Review Letters. 84 (6): 1156–1159. arXiv:chao-dyn/9905039. Bibcode:2000PhRvL..84.1156T. doi:10.1103/PhysRevLett.84.1156. PMID 11017467. S2CID 25507688.
  21. ^ Takahiro Sagawa & Masahito Ueda (2010). "Generalized Jarzynski Equality under Nonequilibrium Feedback Control". Physical Review Letters. 104 (9): 090602. arXiv:0907.4914. Bibcode:2010PhRvL.104i0602S. doi:10.1103/PhysRevLett.104.090602. PMID 20366975. S2CID 1549122.
  22. ^ Armen E Allahverdyan, Dominik Janzing and Guenter Mahler (2009). "Thermodynamic efficiency of information and heat flow". Journal of Statistical Mechanics: Theory and Experiment. 2009 (9): P09011. arXiv:0907.3320. Bibcode:2009JSMTE..09..011A. doi:10.1088/1742-5468/2009/09/P09011. S2CID 118440998.
  23. ^ Naoto Shiraishi & Takahiro Sagawa (2015). "Fluctuation theorem for partially masked nonequilibrium dynamics". Physical Review E. 91 (1): 012130. arXiv:1403.4018. Bibcode:2015PhRvE..91a2130S. doi:10.1103/PhysRevE.91.012130. PMID 25679593. S2CID 1805888.
  24. ^ Jarillo, Javier; Tangarife, Tomás; Cao, Francisco J. (2016-01-22). "Efficiency at maximum power of a discrete feedback ratchet". Physical Review E. 93 (1): 012142. Bibcode:2016PhRvE..93a2142J. doi:10.1103/PhysRevE.93.012142. PMID 26871058.
  25. ^ Ruiz-Pino, Natalia; Villarrubia-Moreno, Daniel; Prados, Antonio; Cao-García, Francisco J. (2023-09-12). "Information in feedback ratchets". Physical Review E. 108 (3): 034112. arXiv:2303.16804. Bibcode:2023PhRvE.108c4112R. doi:10.1103/PhysRevE.108.034112. PMID 37849167.
  26. ^ Loewenstein, Werner R. (2013-01-29). Physics in mind : a quantum view of the brain. New York: Basic Books. ISBN 9780465029846. OCLC 778420640.
  27. ^ Silagadze, Z. K (2007). "Maxwell's demon through the looking glass". Acta Physica Polonica B. 38 (1): 101–126. arXiv:physics/0608114. Bibcode:2007AcPPB..38..101S.
  28. ^ Serreli, V; Lee, CF; Kay, ER; Leigh, DA (February 2007). "A molecular information ratchet". Nature. 445 (7127): 523–527. Bibcode:2007Natur.445..523S. doi:10.1038/nature05452. PMID 17268466. S2CID 4314051.
  29. ^ Bissell, Richard A; Córdova, Emilio; Kaifer, Angel E.; Stoddart, J. Fraser (12 May 1994). "A chemically and electrochemically switchable molecular shuttle". Nature. 369 (6476): 133–137. Bibcode:1994Natur.369..133B. doi:10.1038/369133a0. S2CID 44926804.
  30. ^ Katharine Sanderson (31 January 2007). "A demon of a device". Nature. doi:10.1038/news070129-10. S2CID 121130699.
  31. ^ Raizen, Mark G. (June 12, 2009). "Comprehensive Control of Atomic Motion". Science. 324 (5933): 1403–1406. Bibcode:2009Sci...324.1403R. doi:10.1126/science.1171506. PMID 19520950. S2CID 10235622.
  32. ^ Raizen, Mark G. (March 2011). "Demons, Entropy, and the Quest for Absolute Zero". Scientific American. 304 (3): 54–59. Bibcode:2011SciAm.304c..54R. doi:10.1038/scientificamerican0311-54. PMID 21438491. Retrieved November 14, 2014.
  33. ^ a b c Orzel, Chad (January 25, 2010). "Single-Photon Cooling: Making Maxwell's Demon". Uncertain Principles. ScienceBlogs website. Retrieved November 14, 2014.
  34. ^ Koski, J.V.; Maisi, V.F.; Sagava, T.; Pekola, J.P. (14 July 2014). "Experimental Observation of the Role of Mutual Information in the Nonequilibrium Dynamics of a Maxwell Demon". Physical Review Letters. 113 (3): 030601. arXiv:1405.1272. Bibcode:2014PhRvL.113c0601K. doi:10.1103/PhysRevLett.113.030601. PMID 25083623. S2CID 119311588.
  35. ^ Koski, J.V.; Maisi, V.F.; Pekola, J.P.; Averin, D.V. (23 Sep 2014). "Experimental realization of a Szilard engine with a single electron". Proceedings of the National Academy of Sciences of the United States of America. 111 (38): 13786–9. arXiv:1402.5907. Bibcode:2014PNAS..11113786K. doi:10.1073/pnas.1406966111. PMC 4183300. PMID 25201966.
  36. ^ Strasberg, P.; Schaller, G.; Brandes, T.; Esposito, M. (24 Jan 2013). "Thermodynamics of a Physical Model Implementing a Maxwell Demon". Physical Review Letters (Submitted manuscript). 110 (4): 040601. arXiv:1210.5661. Bibcode:2013PhRvL.110d0601S. doi:10.1103/PhysRevLett.110.040601. PMID 25166147. S2CID 5782312.
  37. ^ Koski, J.V.; Kutvonen, A.; Khaymovich, I.M.; Ala-Nissila, T.; Pekola, J.P. (2015). "On-Chip Maxwell's Demon as an Information-Powered Refrigerator". Physical Review Letters. 115 (26): 260602. arXiv:1507.00530. Bibcode:2015PhRvL.115z0602K. doi:10.1103/PhysRevLett.115.260602. PMID 26764980. S2CID 3393380.
  38. ^ Koski, J.V.; Pekola, J.P. (16 December 2016). "Maxwell's demons realized in electronic circuits". Comptes Rendus Physique. 17 (10): 1130–1138. Bibcode:2016CRPhy..17.1130K. doi:10.1016/j.crhy.2016.08.011.
  39. ^ Pekola, J.P.; Golubev, D.S.; Averin, D.V. (5 Jan 2016). "Maxwell's demon based on a single qubit". Physical Review B. 93 (2): 024501. arXiv:1508.03803. Bibcode:2016PhRvB..93b4501P. doi:10.1103/PhysRevB.93.024501. S2CID 55523206.
  40. ^ Fernando J. Corbató (2002-01-23). "Take Our Word for It". Retrieved 2006-08-20.
  41. ^ Cater (1947), pp. 640–647; see also Daub (1970), reprinted in Leff & Rex (1990), pp. 37–51.
  42. ^ Adams (1919), p. 267.

References

[edit]
  • Cater, H. D., ed. (1947). Henry Adams and his Friends. Boston.
  • Daub, E. E. (1967). "Atomism and Thermodynamics". Isis. 58 (3): 293–303. doi:10.1086/350264. S2CID 143459461.
  • Leff, Harvey S. & Andrew F. Rex, ed. (1990). Maxwell's Demon: Entropy, Information, Computing. Bristol: Adam-Hilger. ISBN 978-0-7503-0057-5.
  • Leff, Harvey S. & Andrew F. Rex, ed. (2002). Maxwell's Demon 2: Entropy, Classical and Quantum Information, Computing. CRC Press. ISBN 978-0-7503-0759-8.
  • Adams, H. (1919). The Degradation of the Democratic Dogma. New York: Kessinger. ISBN 978-1-4179-1598-9.
[edit]
Wikiquote has quotations related to Maxwell's demon.
Retrieved from "https://en.wikipedia.org/enwiki/w/index.php?title=Maxwell%27s_demon&oldid=1258883874"