File:Numerical integration illustration, h=0.25.png
Appearance
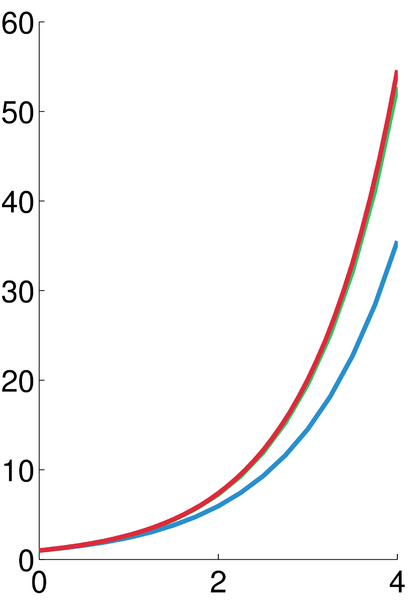
Size of this preview: 412 × 600 pixels. Other resolutions: 165 × 240 pixels | 330 × 480 pixels | 528 × 768 pixels | 703 × 1,024 pixels | 1,500 × 2,183 pixels.
Original file (1,500 × 2,183 pixels, file size: 85 KB, MIME type: image/png)
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 03:02, 25 May 2007 |  | 1,500 × 2,183 (85 KB) | Oleg Alexandrov | Make exact solution smooth |
| 05:00, 20 May 2007 |  | 1,500 × 2,183 (84 KB) | Oleg Alexandrov | Higher resolution. Same license. | |
| 03:19, 20 May 2007 |  | 375 × 546 (16 KB) | Oleg Alexandrov | {{Information |Description=Illustration of Numerical ordinary differential equations |Source=self-made |Date= |Author= User:Oleg Alexandrov }} Category:Numerical analysis {{PD-self}} |
File usage
No pages on the English Wikipedia use this file (pages on other projects are not listed).
Global file usage
The following other wikis use this file:
- Usage on ca.wikipedia.org
- Usage on el.wikipedia.org
- Usage on it.wikipedia.org
- Usage on mn.wikipedia.org
- Usage on pt.wikipedia.org
- Usage on tl.wikipedia.org
- Usage on uk.wikipedia.org
- Usage on zh.wikipedia.org