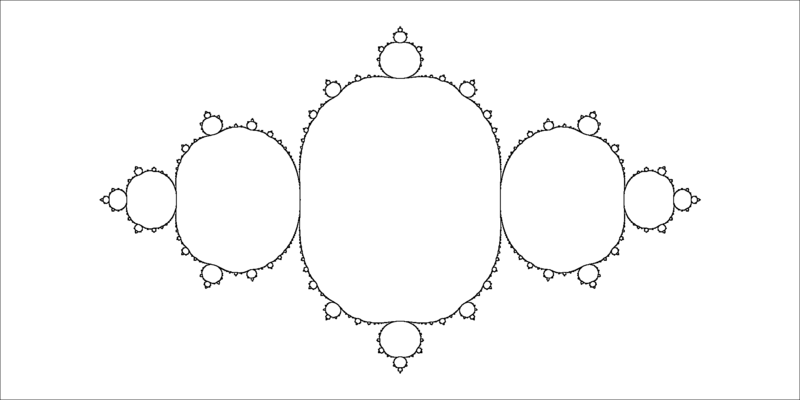
Size of this preview: 800 × 400 pixels. Other resolutions: 320 × 160 pixels | 640 × 320 pixels | 1,024 × 512 pixels | 2,000 × 1,000 pixels.

Original file (2,000 × 1,000 pixels, file size: 9 KB, MIME type: image/png)

This is a file from the Wikimedia Commons. Information from its description page there is shown below.
Commons is a freely licensed media file repository. You can help.

Summary

DescriptionParabolic julia set c=-0.75.png	English: Parabolic julia set for fc(z) = z^2 + c with c=-3/4. Internal angle p/q = 1/2. This Julia set is called Basilica or San Marco Fractal because its shape reminds reflection of the San Marco Cathedral in the flooded streets of Venice. Français : Ensemble de Julia pour for fc(z) = z^2 + c avec c=-3/4. Angle interne p/q = 1/2. Cet ensemble fractal est appelé Basilica ou San Marco parce que sa forme rappelle la réflexion de la basilique Saint-Marc dans les rues inondées de Venise.
Source	Own work
Author	Adam majewski

Long description

Discrete dynamical system

Planes and arrays

This is an image of rectangle part from dynamic plane described by corners :

const double ZxMin=-2.0;
const double ZxMax=2.0;
const double ZyMin=-1.0;
const double ZyMax=1.0;

It is rasterised on screen/memory pixel ( or elements of 2D array) :

#define iXmax 2000 /* height of image in pixels */
#define iYmax 1000

Making the image

For each pixel ( iX, iY) of above image ( = element of data array) program computes it's color :

/* pseudocode */
for(iY=0;iY<iYmax;++iY)
 for(iX=0;iX<iXmax;++iX){
   i = f(iX,iY); // index of the array ( both data and edge)
   data[i]=color( iX, iY)
   }

Then finds edges in data array and saves them to the edge array and saves the edge array to pgm file.

Computing color

Equivalent maps =

$g(z)=z(1-z^{2})=z-z^{3}$ ^[1]
$f_{c}(z)=z^{2}-{\frac {3}{4}}$ where $c=-{\frac {3}{4}}$
$f_{\lambda }(z)=z^{2}+\lambda z=z^{2}-z$ where $\lambda =-1$

One can check it with Xaos Menu : Fractal/User Formula

Licensing

I, the copyright holder of this work, hereby publish it under the following licenses:

This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.

You are free:

to share – to copy, distribute and transmit the work
to remix – to adapt the work

Under the following conditions:

attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.

Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version published by the Free Software Foundation; with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts. A copy of the license is included in the section entitled GNU Free Documentation License.

You may select the license of your choice.

C src code

Source code was formatted with Emacs

/*

  c console program
  -----------------------------------------
  1.ppm file code is  based on the code of Claudio Rocchini
  http://en.wikipedia.org/wiki/Image:Color_complex_plot.jpg
  create 24 bit color graphic file ,  portable pixmap file = PPM 
  see http://en.wikipedia.org/wiki/Portable_pixmap
  to see the file use external application ( graphic viewer)
  I think that creating graphic can't be simpler
  ---------------------------
  2. first it creates data array which is used to store rgb color values of pixels,
  fills tha array with data and after that writes the data from array to pgm file.
  It alows free ( non sequential) acces to "pixels"
    
  -------------------------------------------
  Adam Majewski   fraktal.republika.pl 
 
  Sobel filter 
  Gh = sum of six values ( 3 values of matrix are equal to 0 ). Each value is = pixel_color * filter_coefficients 


  gcc t.c -lm -Wall -o2
  gcc t.c -lm -Wall -march=native
  ./a.out


 
*/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <complex.h>
#include <string.h>

/* iXmax/iYmax = 1 */
#define iXmax 2000 /* height of image in pixels */
#define iYmax 1000
/* fc(z) = z*z + c */
#define denominator 2 /* denominator of internal angle */
#define Cx -0.75 /* C = Cx + Cy*i */
#define Cy  0.0
#define AR 0.0014998955  /* PixelWidth*1.5   radius of circle around attractor ZA = target set for attracting points */
#define AR2 AR*AR
//#define alfa (1-sqrt(1-4*Cx))/2 /* attracting or parabolic fixed point z = alfa */
//#define beta (1+sqrt(1-4*Cx))/2 /* repelling or parabolic fixed point z = beta */

/* escape time to infinity */
int GiveExtLastIteration(double _Zx0, double _Zy0,double C_x, double C_y, int iMax, double _ER2)
{ 
  int i;
  double Zx, Zy;
  double Zx2, Zy2; /* Zx2=Zx*Zx;  Zy2=Zy*Zy  */
  Zx=_Zx0; /* initial value of orbit  */
  Zy=_Zy0;
  Zx2=Zx*Zx;
  Zy2=Zy*Zy;
  for (i=0;i<iMax && ((Zx2+Zy2)<_ER2);i++)
    {
      Zy=2*Zx*Zy + C_y;
      Zx=Zx2-Zy2 +C_x;
      Zx2=Zx*Zx;
      Zy2=Zy*Zy;
    };
  return i;
}


/* find attractor ZA  using forward iteration of critical point Z = 0  */
/* if period is >1 gives one point from attracting cycle */
double complex GiveAttractor(double _Cx, double _Cy, double ER2, int _IterationMax)
{
  int Iteration;
  double Zx, Zy; /* z = zx+zy*i */
  double Zx2, Zy2; /* Zx2=Zx*Zx;  Zy2=Zy*Zy  */
  /* -- find attractor ZA  using forward iteration of critical point Z = 0  */
  Zx=0.0;
  Zy=0.0;
  Zx2=Zx*Zx;
  Zy2=Zy*Zy;
  for (Iteration=0;Iteration<_IterationMax && ((Zx2+Zy2)<ER2);Iteration++)
    {
      Zy=2*Zx*Zy + _Cy;
      Zx=Zx2-Zy2 + _Cx;
      Zx2=Zx*Zx;
      Zy2=Zy*Zy;
    };
  return Zx+Zy*I;
}

/* attracting time to finite attractor ZA */
int GiveIntLastIteration(double _Zx0, double _Zy0,double C_x, double C_y, int iMax, double _AR2, double _ZAx, double _ZAy )
{ 
  int i;
  double Zx, Zy; /* z = zx+zy*i */
  double Zx2, Zy2; /* Zx2=Zx*Zx;  Zy2=Zy*Zy  */
  double d, dX, dY; /* distance from z to Alpha  */
  Zx=_Zx0; /* initial value of orbit  */
  Zy=_Zy0;
  Zx2=Zx*Zx;
  Zy2=Zy*Zy;
  dX=Zx-_ZAx;
  dY=Zy-_ZAy;
  d=dX*dX+dY*dY;
  for (i=0;i<iMax && (d>_AR2);i++)
    {
      Zy=2*Zx*Zy + C_y;
      Zx=Zx2-Zy2 +C_x;
      Zx2=Zx*Zx;
      Zy2=Zy*Zy;
      dX=Zx-_ZAx;
      dY=Zy-_ZAy;
      d=dX*dX+dY*dY;
    };
  return i;
}

/* gives position of point (iX,iY) in 1D array  ; uses also global variables */
unsigned int f(unsigned int _iX, unsigned int _iY)
{return (_iX + (iYmax-_iY-1)*iXmax );}

/* --------------------------------------------------------------------------------------------------------- */

int main(){
  
 
    
  unsigned int iX,iY, /* indices of 2D virtual array (image) = integer coordinate */
    i, /* index of 1D array  */
    iLength = iXmax*iYmax;/* length of array in bytes = number of bytes = number of pixels of image * number of bytes of color */
  /* world ( double) coordinate = parameter plane*/
  const double ZxMin=-2.0;
  const double ZxMax=2.0;
  const double ZyMin=-1.0;
  const double ZyMax=1.0;
  double PixelWidth=(ZxMax-ZxMin)/iXmax;
  double PixelHeight=(ZyMax-ZyMin)/iYmax;
  /* */
  double Zx, Zy;    /* Z=Zx+Zy*i   */
  double complex ZA;  /* atractor ZA = ZAx + ZAy*i */
  /* */
  
  const double EscapeRadius=2.0; /* radius of circle around origin; its complement is a target set for escaping points */
  double ER2=EscapeRadius*EscapeRadius;
  
  const int IterationMax=60,
    IterationMaxBig= 1000001;
  int eLastIteration, iLastIteration;
  /* sobel filter */
  unsigned char G, Gh, Gv; 
  /* color */
  unsigned char color[]={255,230,180}; /* shades of gray used in image */
  const unsigned int MaxColorComponentValue=255; /* color component is coded from 0 to 255 ;  it is 8 bit color file */
  

  /* dynamic 1D arrays for colors ( shades of gray ) */
  unsigned char *data, *edge;
  data = malloc( iLength * sizeof(unsigned char) );
  edge = malloc( iLength * sizeof(unsigned char) );
  if (data == NULL || edge==NULL)
    {
      fprintf(stderr," Could not allocate memory");
      getchar(); 
      return 1;
    }
  else printf(" memory is OK\n");


   
 
  
  ZA = GiveAttractor( Cx, Cy, ER2, IterationMaxBig); /* find attractor ZA  using forward iteration of critical point Z = 0  */



  printf(" fill the data array \n");
  for(iY=0;iY<iYmax;++iY){ 
    Zy=ZyMin + iY*PixelHeight; /*  */
    if (fabs(Zy)<PixelHeight/2) Zy=0.0; /*  */
    printf(" row %u from %u \n",iY, iYmax);    
    for(iX=0;iX<iXmax;++iX){ 
      Zx=ZxMin + iX*PixelWidth;
      eLastIteration = GiveExtLastIteration(Zx, Zy, Cx, Cy, IterationMax, ER2 );
      i= f(iX,iY); /* compute index of 1D array from indices of 2D array */
      if ( IterationMax != eLastIteration ) 
	{data[i]=245;} /* exterior */
      else /* interior */
	{ iLastIteration = GiveIntLastIteration(Zx, Zy, Cx, Cy, IterationMaxBig, AR2, creal(ZA), cimag(ZA));
          data[i]=color[iLastIteration % denominator];} /*  level sets of attraction time */
      /*  if (Zx>0 && Zy>0) data[i]=255-data[i];    check the orientation of Z-plane by marking first quadrant */
    }
  }


  printf(" find boundaries in data array using  Sobel filter\n");   

  for(iY=1;iY<iYmax-1;++iY){ 
    for(iX=1;iX<iXmax-1;++iX){ 
      Gv= data[f(iX-1,iY+1)] + 2*data[f(iX,iY+1)] + data[f(iX-1,iY+1)] - data[f(iX-1,iY-1)] - 2*data[f(iX-1,iY)] - data[f(iX+1,iY-1)];
      Gh= data[f(iX+1,iY+1)] + 2*data[f(iX+1,iY)] + data[f(iX-1,iY-1)] - data[f(iX+1,iY-1)] - 2*data[f(iX-1,iY)] - data[f(iX-1,iY-1)];
      G = sqrt(Gh*Gh + Gv*Gv);
      i= f(iX,iY); /* compute index of 1D array from indices of 2D array */
      if (G==0) {edge[i]=255;} /* background */
      else {edge[i]=0;}  /* boundary */
    }
  }

  //  printf(" copy boundaries from edge to data array \n");
  //  for(iY=1;iY<iYmax-1;++iY){ 
  //   for(iX=1;iX<iXmax-1;++iX)
  //    {i= f(iX,iY); /* compute index of 1D array from indices of 2D array */
  //	if (edge[i]==0) data[i]=0;}}


  /* ---------- file  -------------------------------------*/
  printf(" save  data array to the file \n");
  FILE * fp;
  char name [10]; /* name of file */
  i = sprintf(name,"B%2.9f",AR); /* result (is saved in i) but is not used */
  char *filename =strcat(name,".pgm");
  char *comment="# C=0.2";/* comment should start with # */
  /* save image to the pgm file  */      
  fp= fopen(filename,"wb"); /*create new file,give it a name and open it in binary mode  */
  fprintf(fp,"P5\n %s\n %u\n %u\n %u\n",comment,iXmax,iYmax,MaxColorComponentValue);  /*write header to the file*/
  fwrite(edge,iLength,1,fp);  /*write image data bytes to the file in one step */
  printf("File %s saved. \n", filename);
  fclose(fp);


  /* --------------free memory ---------------------*/
  free(data);
  free(edge);
  
  

  return 0;
}

Fragmentarium src code

#include "2D.frag"
#group Julia set

// maximal number of iterations = quality of image
// but also ability to fall into circlae with radius ar
// around alfa fixed point
// if to big then all not escaping points are  unknown ( green)
uniform int iMax; slider[1,1000,10000]
// escape radius = er;  er2= er*er >= 4.0
uniform float er2; slider[4.0,100.0,1000.0]
// attrating radius (around fixed point alfa) = ar ;  ar2 = ar*ar
uniform float ar2; slider[0.000001,0.0001,0.003]
//
//uniform float m; slider[0.0,1.0,1000.0]

vec2 c = vec2(-0.75,0.0);  // initial value of c
vec2 za = vec2(-0.5,0.0); // alfa fixed point




vec3 GiveColor( int type)
{
	switch (type)
	{
		case 0:  return vec3(1.0, 0.0, 0.0); break; //unknown
		case 1:  return vec3(0.0, 1.0, 0.0); break; // interior right
           case 2:  return vec3(0.0, 0.0, 1.0); break; // interior left
		case 3:  return vec3(1.0, 1.0, 1.0); break; // exterior
		default: 	return vec3(1.0, 0.0,0.0); 	break;}
}



// compute color of pixel = main function here
vec3 color(vec2 z0) {
	
	
	
	
	vec2 z=z0;
	int type=0; 
   // 0 =unknown; interior right =1; interior left = 2
 // exterior =3;
	int i=0; // number of iteration
	
	// iteration
	for ( i = 0; i < iMax; i++) {
		
		// escape test
		if (dot(z,z)> er2)               { type = 3; break;}// exterior
		// attraction test
		if ((dot(z-za,z-za)< ar2)  && (i % 2) )  
           {
           

          if (z.x>za.x) { type = 1; break;}// interior right
            else { type = 2; break;}// interior right
           }
     
		z = vec2(z.x*z.x-z.y*z.y,2*z.x*z.y) +  c; // z= z^2+c
	}
	
	return GiveColor(type);
	
}

References

↑ Note on dynamically stable perturbations of parabolics by Tomoki Kawahira archive copy at the Wayback Machine

File history

Click on a date/time to view the file as it appeared at that time.

	Date/Time	Thumbnail	Dimensions	User	Comment
current	19:21, 30 May 2014		2,000 × 1,000 (9 KB)	JeffyP	I'm here to make the world a smaller place ☺
	16:59, 13 January 2012		2,000 × 1,000 (11 KB)	Soul windsurfer	{{Information \|Description ={{en\|1=Parabolic julia set c=-3/4}} \|Source ={{own}} \|Author =Adam majewski \|Date = \|Permission = \|other_versions = }}

File usage

No pages on the English Wikipedia use this file (pages on other projects are not listed).

Global file usage

The following other wikis use this file:

Usage on en.wikibooks.org
Usage on ja.wikipedia.org
- ジュリア集合

[1] Note on dynamically stable perturbations of parabolics by Tomoki Kawahira archive copy at the Wayback Machine

[1]

File:Parabolic julia set c=-0.75.png

Contents

Summary

Long description

Discrete dynamical system

Planes and arrays

Making the image

Computing color

Equivalent maps =

Licensing

C src code

Fragmentarium src code

References

Captions

Items portrayed in this file

depicts

creator

some value

copyright status

copyrighted

copyright license

GNU Free Documentation License, version 1.2 or later

Creative Commons Attribution-ShareAlike 3.0 Unported

source of file

original creation by uploader

File history

File usage

Global file usage