Diferencia entre revisiones de «Distribución de Cauchy»
Sin resumen de edición |
m Reemplazos con Replacer: «coíncide» + mejoras cosméticas |
||
| (No se muestran 31 ediciones intermedias de 25 usuarios) | |||
| Línea 1: | Línea 1: | ||
<gallery> |
|||
</gallery> |
|||
{{Ficha de distribución de probabilidad | |
{{Ficha de distribución de probabilidad | |
||
nombre =Cauchy-Lorentz| |
nombre =Cauchy-Lorentz| |
||
| Línea 21: | Línea 18: | ||
car =<math>\exp(x_0\,i\,t-\gamma\,|t|)\!</math> |
car =<math>\exp(x_0\,i\,t-\gamma\,|t|)\!</math> |
||
}} |
}} |
||
La '''distribución Cauchy-Lorentz''', llamada en honor a [[Cauchy|Augustin Cauchy]] y [[Hendrik Lorentz]], es una [[distribución de probabilidad]] continua. Es conocida como la '''distribución de Cauchy''' y en el ámbito de la física se conoce como la '''distribución de Lorentz''', la '''función Lorentziana''' |
La '''distribución Cauchy-Lorentz''', llamada en honor a [[Cauchy|Augustin Cauchy]] y [[Hendrik Lorentz]], es una [[distribución de probabilidad]] continua. Es conocida como la '''distribución de Cauchy''' y en el ámbito de la física se conoce como la '''distribución de Lorentz''', la '''función Lorentziana''' o la [[Distribución de Breit-Wigner|distribución de '''Breit-Wigner''']]. Su importancia en la [[física]] es dada por ser la solución de la [[ecuación diferencial]] que describe la [[wikt:es:resonancia|resonancia]] forzada. En [[espectroscopia]] describe la forma de las líneas espectrales que son ampliadas por diversos mecanismos, en particular, el mecanismo de [https://web.archive.org/web/20071217221820/http://www.astro.puc.cl/~dante/cursofia2000/apuntes/node55.html ensanchamiento por colisión]. |
||
==Caracterización== |
==Caracterización== |
||
=== Función de densidad |
=== Función de densidad === |
||
En [[estadística]] la '''distribución de Cauchy''' (a veces también ''distribución de Lorentz'') es una [[distribución de probabilidad]] continua cuya [[función de densidad]] es |
En [[estadística]] la '''distribución de Cauchy''' (a veces también ''distribución de Lorentz'') es una [[distribución de probabilidad]] continua cuya [[función de densidad]] es |
||
| Línea 32: | Línea 29: | ||
\end{align}</math> |
\end{align}</math> |
||
donde ''x''<sub>0</sub> es el parámetro de corrimiento que |
donde ''x''<sub>0</sub> es el parámetro de corrimiento que específica la ubicación del pico de la distribución, y ''γ'' es el parámetro de escala que específica el ancho medio al máximo medio (half-width at half-maximum, HWHM). |
||
En el caso especial donde ''x''<sub>0</sub> = 0 y ''γ'' = 1 es denominado la '''distribución estándar Cauchy''' con la función de densidad de probabilidad |
En el caso especial donde ''x''<sub>0</sub> = 0 y ''γ'' = 1 es denominado la '''distribución estándar Cauchy''' con la función de densidad de probabilidad |
||
| Línea 43: | Línea 40: | ||
=== Función de distribución === |
=== Función de distribución === |
||
La función de distribución acumulativa (CDF) es: |
La función de distribución acumulativa (CDF) es: |
||
| Línea 52: | Línea 50: | ||
==Propiedades== |
==Propiedades== |
||
La distribución de Cauchy es un ejemplo de una distribución que no tiene [[esperanza matemática|valor esperado]], [[varianza]] o [[momento (matemáticas)|momentos]] definidos. Su [[Moda (estadística)|moda]] y su [[mediana]] están bien definidas y son ambas iguales a x<sub>0</sub>. |
La distribución de Cauchy es un ejemplo de una distribución que no tiene [[esperanza matemática|valor esperado]], [[varianza]] o [[momento (matemáticas)|momentos]] definidos. Su [[Moda (estadística)|moda]] y su [[Mediana (estadística)|mediana]] están bien definidas y son ambas iguales a x<sub>0</sub>. |
||
Cuando ''U'' y ''V'' son dos variables aleatorias |
Cuando ''U'' y ''V'' son dos variables aleatorias independientes y [[Distribución normal|normalmente distribuidas]] con un [[Media aritmética|valor esperado]] = 0 y una [[varianza]] = 1, luego la tasa''U''/''V'' tiene la distribución estándar de Cauchy. |
||
Sí ''X''<sub>1</sub>, …, ''X''<sub>''n''</sub> son variables aleatorias, independientes e idénticamente distribuidas, cada una con una distribución Cauchy, luego la [[Media aritmética|media de la muestra]] (''X''<sub>1</sub> + … + ''X''<sub>''n''</sub>)/''n'' tiene la misma distribución Cauchy estándar (la media de la muestra, la |
Sí ''X''<sub>1</sub>, …, ''X''<sub>''n''</sub> son variables aleatorias, independientes e idénticamente distribuidas, cada una con una distribución Cauchy, luego la [[Media aritmética|media de la muestra]] (''X''<sub>1</sub> + … + ''X''<sub>''n''</sub>)/''n'' tiene la misma distribución Cauchy estándar (la media de la muestra, la cual no es afectada por los valores extremos, puede ser usada como medida de la tendencia central). Para comprobar que esto es cierto se calcula la [[función característica]] de la media de la muestra: |
||
:<math>\phi_{\overline{X}}(t) = \mathrm{E}\left(e^{i\,\overline{X}\,t}\right) \,\!</math> |
:<math>\phi_{\overline{X}}(t) = \mathrm{E}\left(e^{i\,\overline{X}\,t}\right) \,\!</math> |
||
donde <math>\overline{X}</math> es la media de la muestra. Este ejemplo sirve para demostrar que la hipótesis de |
donde <math>\overline{X}</math> es la media de la muestra. Este ejemplo sirve para demostrar que la hipótesis de varianza finita en el [[teorema del límite central]] no puede ser depuesta, al igual que la hipótesis de esperanza finita en la [[ley de los grandes números]]. Es también un ejemplo de una versión más generalizada del teorema de límite central que es característica de todas las distribuciones asimétricas alpha-estables de [[Paul Pierre Lévy|Lévy]], de las cuales es la distribución de Cauchy un caso especial. |
||
La distribución de Cauchy es una función de distribución [[divisibilidad infinita|infinitamente divisible]]. Es también una distribución estrictamente [[estabilidad (probabilidad)|estable]]. |
La distribución de Cauchy es una función de distribución [[divisibilidad infinita|infinitamente divisible]]. Es también una distribución estrictamente [[estabilidad (probabilidad)|estable]]. |
||
La distribución de Cauchy |
La distribución de Cauchy coincide con la [[distribución t de Student]] con un grado de libertad. |
||
<!-- ¿ cómo traducir "location-scale family ? |
<!-- ¿ cómo traducir "location-scale family ? |
||
| Línea 79: | Línea 77: | ||
:<math>\phi_x(t; x_0,\gamma) = \mathrm{E}(e^{i\,X\,t}) = \exp(i\,x_0\,t-\gamma\,|t|). \!</math> |
:<math>\phi_x(t; x_0,\gamma) = \mathrm{E}(e^{i\,X\,t}) = \exp(i\,x_0\,t-\gamma\,|t|). \!</math> |
||
[[Archivo:Cauchy distribution.png|thumb|250px|Aplicación de la distribución de probabilidad acumulada de Cauchy a lluvias diárias máximas.<ref> CumFreq software para adecuación de distribuciones de probabilidad [https://www.waterlog.info/cumfreq.htm]</ref> ]] |
|||
| ⚫ | |||
==Aplicación== |
|||
*En la [[hidrología]], se utiliza la distribución de Cauchy para analizar [[Variable aleatoria|variables aleatorias]] como valores máximos de la precipitación y la descarga de ríos,<ref name = "Oosterbaan">{{cite book|editor-last=Ritzema |editor-first=H.P. |first1=R.J. |last1=Oosterbaan |chapter=Chapter 6 Frequency and Regression Analysis|year=1994 |title=Drainage Principles and Applications, Publication 16 |publisher=International Institute for Land Reclamation and Improvement (ILRI) |location=Wageningen, The Netherlands |pages=175–224 |url=http://www.waterlog.info/pdf/freqtxt.pdf |isbn=90-70754-33-9}}</ref> y además para describir épocas de sequía.<ref>{{cite journal |doi=10.1016/j.jhydrol.2010.04.035 |title=An extreme value analysis of UK drought and projections of change in the future |year=2010 |last1=Burke |first1=Eleanor J. |last2=Perry |first2=Richard H.J. |last3=Brown |first3=Simon J. |journal=Journal of Hydrology |volume=388 |pages=131}}</ref> |
|||
::La imagen azul ilustra un ejemplo del ajuste de la distribución de Cauchy a las lluvias máximas diarias ordenadas, mostrando también la franja de 90% de [[Intervalo de confianza|confianza]], basada en la [[distribución binomial]]. Las observaciones presentan los [[Gráfico Q-Q|marcadores de posición]], como parte del análisis de [[Frecuencia estadística|frecuencia acumulada]]. |
|||
==Véase también== |
|||
* [[Parametrización de McCullagh de las distribuciones de Cauchy]] |
|||
== Referencias == |
|||
{{listaref}} |
|||
| ⚫ | |||
* {{MathWorld|CauchyDistribution|CauchyDistribution}} |
* {{MathWorld|CauchyDistribution|CauchyDistribution}} |
||
* [http://www.gnu.org/software/gsl/manual/gsl-ref.html#SEC294 GNU Scientific Library - Reference Manual] |
* [http://www.gnu.org/software/gsl/manual/gsl-ref.html#SEC294 GNU Scientific Library - Reference Manual] |
||
* [http://www.astro.puc.cl/~dante/cursofia2000/apuntes/node55.html ensanchamiento por colisión] |
* [https://web.archive.org/web/20071217221820/http://www.astro.puc.cl/~dante/cursofia2000/apuntes/node55.html ensanchamiento por colisión] |
||
* [http://www.estadistico.com/dic.html Diccionario Estadístico] (DEAD LINK) |
|||
* [http://www.elektro-energetika.cz/calculations/distrcauchy.php?language=espanol Calculadora Distribución de Cauchy] |
* [http://www.elektro-energetika.cz/calculations/distrcauchy.php?language=espanol Calculadora Distribución de Cauchy] |
||
{{ORDENAR:Cauchy}} |
|||
{{Control de autoridades}} |
|||
[[Categoría:Distribuciones continuas]] |
[[Categoría:Distribuciones continuas]] |
||
[[Categoría:Epónimos relacionados con las matemáticas]] |
[[Categoría:Epónimos relacionados con las matemáticas|Cauchy, distribución]] |
||
[[Categoría:Augustin Louis Cauchy]] |
|||
Revisión actual - 19:32 3 jul 2023
| Cauchy-Lorentz | ||
|---|---|---|
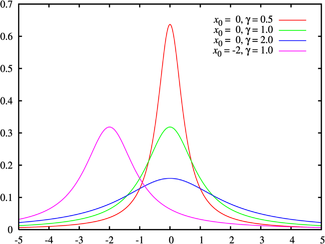 La línea verde es la distribución estándar de Cauchy Función de densidad de probabilidad | ||
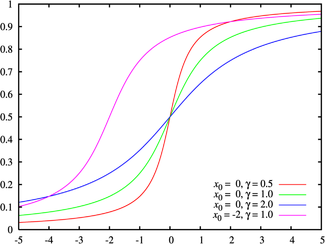 Leyenda de colores para la PDF de la imagen superior Función de distribución de probabilidad | ||
| Parámetros |
(real) escala (real) | |
| Función de densidad (pdf) | ||
| Función de distribución (cdf) | ||
| Media | no definida | |
| Mediana | ||
| Moda | ||
| Varianza | no definida | |
| Curtosis | no definida | |
| Entropía | ||
| Función generadora de momentos (mgf) | no definida | |
| Función característica | ||
La distribución Cauchy-Lorentz, llamada en honor a Augustin Cauchy y Hendrik Lorentz, es una distribución de probabilidad continua. Es conocida como la distribución de Cauchy y en el ámbito de la física se conoce como la distribución de Lorentz, la función Lorentziana o la distribución de Breit-Wigner. Su importancia en la física es dada por ser la solución de la ecuación diferencial que describe la resonancia forzada. En espectroscopia describe la forma de las líneas espectrales que son ampliadas por diversos mecanismos, en particular, el mecanismo de ensanchamiento por colisión.
Caracterización
[editar]Función de densidad
[editar]En estadística la distribución de Cauchy (a veces también distribución de Lorentz) es una distribución de probabilidad continua cuya función de densidad es
donde x0 es el parámetro de corrimiento que específica la ubicación del pico de la distribución, y γ es el parámetro de escala que específica el ancho medio al máximo medio (half-width at half-maximum, HWHM).
En el caso especial donde x0 = 0 y γ = 1 es denominado la distribución estándar Cauchy con la función de densidad de probabilidad
En general la distribución de Cauchy no tiene valor esperado ni varianza.
Sean y dos variables aleatorias uniformes dentro -1 y 1 y , entonces el número tiene la distribución Cauchy.
Función de distribución
[editar]La función de distribución acumulativa (CDF) es:
y la función inversa de distribución acumulativa para la distribución Cauchy es
Propiedades
[editar]La distribución de Cauchy es un ejemplo de una distribución que no tiene valor esperado, varianza o momentos definidos. Su moda y su mediana están bien definidas y son ambas iguales a x0.
Cuando U y V son dos variables aleatorias independientes y normalmente distribuidas con un valor esperado = 0 y una varianza = 1, luego la tasaU/V tiene la distribución estándar de Cauchy.
Sí X1, …, Xn son variables aleatorias, independientes e idénticamente distribuidas, cada una con una distribución Cauchy, luego la media de la muestra (X1 + … + Xn)/n tiene la misma distribución Cauchy estándar (la media de la muestra, la cual no es afectada por los valores extremos, puede ser usada como medida de la tendencia central). Para comprobar que esto es cierto se calcula la función característica de la media de la muestra:
donde es la media de la muestra. Este ejemplo sirve para demostrar que la hipótesis de varianza finita en el teorema del límite central no puede ser depuesta, al igual que la hipótesis de esperanza finita en la ley de los grandes números. Es también un ejemplo de una versión más generalizada del teorema de límite central que es característica de todas las distribuciones asimétricas alpha-estables de Lévy, de las cuales es la distribución de Cauchy un caso especial.
La distribución de Cauchy es una función de distribución infinitamente divisible. Es también una distribución estrictamente estable.
La distribución de Cauchy coincide con la distribución t de Student con un grado de libertad.
Función Característica
[editar]Sea X una variable aleatoria con una distribución Cauchy. Luego la función característica de la distribución Cauchy está bien definida:

Aplicación
[editar]- En la hidrología, se utiliza la distribución de Cauchy para analizar variables aleatorias como valores máximos de la precipitación y la descarga de ríos,[2] y además para describir épocas de sequía.[3]
- La imagen azul ilustra un ejemplo del ajuste de la distribución de Cauchy a las lluvias máximas diarias ordenadas, mostrando también la franja de 90% de confianza, basada en la distribución binomial. Las observaciones presentan los marcadores de posición, como parte del análisis de frecuencia acumulada.
Véase también
[editar]Referencias
[editar]- ↑ CumFreq software para adecuación de distribuciones de probabilidad [1]
- ↑ Oosterbaan, R.J. (1994). «Chapter 6 Frequency and Regression Analysis». En Ritzema, H.P., ed. Drainage Principles and Applications, Publication 16. Wageningen, The Netherlands: International Institute for Land Reclamation and Improvement (ILRI). pp. 175-224. ISBN 90-70754-33-9.
- ↑ Burke, Eleanor J.; Perry, Richard H.J.; Brown, Simon J. (2010). «An extreme value analysis of UK drought and projections of change in the future». Journal of Hydrology 388: 131. doi:10.1016/j.jhydrol.2010.04.035.
Enlaces externos
[editar]- Weisstein, Eric W. «CauchyDistribution». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- GNU Scientific Library - Reference Manual
- ensanchamiento por colisión
- Calculadora Distribución de Cauchy



![{\displaystyle {\frac {1}{\pi \gamma \,\left[1+\left({\frac {x-x_{0}}{\gamma }}\right)^{2}\right]}}\!}](https://wikimedia.org/eswiki/api/rest_v1/media/math/render/svg/2fa7448ba911130c1e33621f1859393d3f00af5c)




![{\displaystyle {\begin{aligned}f(x;x_{0},\gamma )&={\frac {1}{\pi \gamma \left[1+\left({\frac {x-x_{0}}{\gamma }}\right)^{2}\right]}}\\[0.5em]&={1 \over \pi }\left[{\gamma \over (x-x_{0})^{2}+\gamma ^{2}}\right]\end{aligned}}}](https://wikimedia.org/eswiki/api/rest_v1/media/math/render/svg/bbede1ef1f334dd0d74bb9773213e89f0412c7c2)






![{\displaystyle F^{-1}(p;x_{0},\gamma )=x_{0}+\gamma \,\tan \left[\pi \,\left(p-{\tfrac {1}{2}}\right)\right].}](https://wikimedia.org/eswiki/api/rest_v1/media/math/render/svg/9d11de58abc0c5eca28e0b5137edbb6c578de719)


