Diferencia entre revisiones de «Cero absoluto»
mSin resumen de edición Etiquetas: Reversión manual Edición visual |
m Revertida una edición de 145.97.177.13 (disc.) a la última edición de SeroBOT Etiqueta: Reversión |
||
| (No se muestran 32 ediciones intermedias de 17 usuarios) | |||
| Línea 1: | Línea 1: | ||
[[Archivo:CelsiusKelvin.svg|thumb|right|150px|Cero kelvin ({{esd|−273.15 °C}}) se define como el cero absoluto.]] |
|||
El '''cero absoluto''' es la [[temperatura]] más baja posible. A esta temperatura el nivel de [[energía interna]] del sistema es el más bajo posible, por lo que las moléculas, según la [[mecánica clásica]], carecen de [[movimiento (física)|movimiento]];<ref>{{Google books|mQBSfR6KZHsC|Pierre J. Rapin – Prontuario del frío|página=5}}</ref> no obstante, según la [[mecánica cuántica]], el cero absoluto debe tener una [[energía]] residual, llamada [[Energía del punto cero|energía de punto cero]], para poder así cumplir el [[principio de indeterminación de Heisenberg]]. |
|||
El cero absoluto sirve de punto de partida tanto para la escala de [[Kelvin]] como para la escala de [[Rankine]].<ref>{{cita libro|apellidos=von Reichenbach|nombre=María Cecilia|título=Cero absoluto. Curiosidades de física|editorial=Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET)|editor=Reichenbach, María Cecilia von|isbn=978-950-692-088-3|páginas=104|apellidos2=Bergero|nombre2=Paula Elena|apellidos3=Álvarez|nombre3=Ariel|apellidos4=del Río|nombre4=Laura|url=http://sedici.unlp.edu.ar/handle/10915/26346|idioma=es}}</ref> |
El '''cero absoluto''' es la [[temperatura]] más baja posible. A esta temperatura el nivel de [[energía interna]] del sistema es el más bajo posible, por lo que las moléculas, según la [[mecánica clásica]], carecen de [[movimiento (física)|movimiento;]]<ref>{{Google books|mQBSfR6KZHsC|Pierre J. Rapin – Prontuario del frío|página=5}}</ref> no obstante, según la [[mecánica cuántica]], el cero absoluto debe tener una [[energía]] residual, llamada [[Energía del punto cero|energía de punto cero]], para poder así cumplir el [[principio de indeterminación de Heisenberg]]. El cero absoluto sirve de punto de partida tanto para la escala de [[Kelvin]] como para la escala de [[Rankine]].<ref>{{cita libro|apellidos=von Reichenbach|nombre=María Cecilia|título=Cero absoluto. Curiosidades de física|editorial=Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET)|editor=Reichenbach, María Cecilia von|isbn=978-950-692-088-3|páginas=104|apellidos2=Bergero|nombre2=Paula Elena|apellidos3=Álvarez|nombre3=Ariel|apellidos4=del Río|nombre4=Laura|url=http://sedici.unlp.edu.ar/handle/10915/26346|idioma=es}}</ref> Así, {{esd|0 [[kelvin|K]]}} (o lo que es lo mismo, {{esd|0 [[Rankine|R]]}}) corresponden, por definición según acuerdo internacional, a la temperatura de {{esd|−273.15 [[grado Celsius|°C]]}} o {{esd|−459.67 [[grado Fahrenheit|°F]]}}.<ref>{{Google books|KFEvYPsc5IMC|Jerry D. Wilson, Anthony J Buffa – Física|página=354}}</ref> |
||
Así, {{unidad|0|[[kelvin|K]]}} (o lo que es lo mismo, {{unidad|0|[[Rankine|R]]}}) corresponden, por definición según acuerdo internacional, a la temperatura de {{unidad|−273,15|[[grado Celsius|°C]]}} o {{unidad|−459,67|[[grado Fahrenheit|°F]]}}.<ref>{{Google books|KFEvYPsc5IMC|Jerry D. Wilson, Anthony J Buffa – Física|página=354}}</ref> |
|||
Según el tercer principio de la [[termodinámica]], el cero absoluto es un [[límite (matemática)|límite]] inalcanzable. En septiembre de 2014, los científicos de la colaboración CUORE en el [[Laboratorio Nacional del Gran Sasso|Laboratori Nazionali del Gran Sasso]] en Italia enfriaron un recipiente de cobre con un volumen de un metro cúbico a {{ |
Según el tercer principio de la [[termodinámica]], el cero absoluto es un [[límite (matemática)|límite]] inalcanzable. En septiembre de 2014, los científicos de la colaboración CUORE en el [[Laboratorio Nacional del Gran Sasso|Laboratori Nazionali del Gran Sasso]] en Italia enfriaron un recipiente de cobre con un volumen de un metro cúbico a {{esd|0.006 K}} ({{esd|−273.144 °C}}) durante {{esd|15 días}}, estableciendo un récord para la temperatura más baja registrada en el universo conocido sobre un volumen contiguo tan grande. La dificultad para llegar a una temperatura tan baja en una cámara de enfriamiento es el hecho que las moléculas de la cámara, al llegar a esa temperatura, no tienen energía suficiente para hacer que esta descienda aún más. |
||
La [[Entropía (termodinámica)|entropía]] de un [[cristal]] ideal puro y perfecto sería cero. Si los átomos que lo componen no forman un cristal perfecto, su entropía debe ser mayor que cero, por lo que la temperatura siempre será superior al cero absoluto y el cristal siempre tendrá imperfecciones inducidas por el movimiento de sus átomos, necesitando un movimiento que lo compense y, por lo tanto, teniendo siempre una imperfección residual. |
La [[Entropía (termodinámica)|entropía]] de un [[cristal]] ideal puro y perfecto sería cero. Si los átomos que lo componen no forman un cristal perfecto, su entropía debe ser mayor que cero, por lo que la temperatura siempre será superior al cero absoluto y el cristal siempre tendrá imperfecciones inducidas por el movimiento de sus átomos, necesitando un movimiento que lo compense y, por lo tanto, teniendo siempre una imperfección residual. |
||
Cabe mencionar que a {{ |
Cabe mencionar que a {{esd|0 K}} absolutamente todas las sustancias conocidas se solidificarían y que según el actual modelo del calor, las moléculas perderían toda capacidad de moverse, vibrar o rotar. |
||
[[Archivo:Gas_thermometer_and_absolute_zero_fr.jpg|miniaturadeimagen|Gráficos de presión en función de la temperatura para tres muestras de gas diferentes en el mismo volumen extrapolado al cero absoluto]] |
|||
| ⚫ | Hasta ahora la temperatura más cercana al cero absoluto ha sido obtenida en laboratorio por científicos del [[Instituto Tecnológico de Massachusetts]] en junio del 2015. Se obtuvo enfriando un gas en un campo magnético hasta {{esd|500 nK}} ({{esd|5 × 10<SUP>−7</SUP> K}}) por encima del cero absoluto.<ref>{{cite web|title=MIT team creates ultracold molecules|url=https://newsoffice.mit.edu/2015/ultracold-molecules-0610|work=Massachusetts Institute of Technology, Massachusetts, Cambridge|fechaacceso=2 de octubre de 2019|urlarchivo=https://web.archive.org/web/20150818112454/http://newsoffice.mit.edu/2015/ultracold-molecules-0610|fechaarchivo=18 de agosto de 2015}}</ref> |
||
Hasta ahora la temperatura más cercana al cero absoluto ha sido |
|||
| ⚫ | obtenida en laboratorio por científicos del [[Instituto Tecnológico de Massachusetts]] en junio del 2015. Se obtuvo enfriando un gas en un campo magnético hasta {{ |
||
== Fenómenos cerca del cero absoluto == |
== Fenómenos cerca del cero absoluto == |
||
| Línea 24: | Línea 22: | ||
| url = http://cdsweb.cern.ch/journal/CERNBulletin/2009/43/News%20Articles/1212977?ln=en |
| url = http://cdsweb.cern.ch/journal/CERNBulletin/2009/43/News%20Articles/1212977?ln=en |
||
| título = CERN Bulletin |
| título = CERN Bulletin |
||
}}<!--Título generado por Muro Bot--></ref> El Gran Colisionador de Hadrones (LHC) alcanza una temperatura de 1 |
}}<!--Título generado por Muro Bot--></ref> El Gran Colisionador de Hadrones (LHC) alcanza una temperatura de 1.9 K. Los experimentos que se llevarán a cabo en este acelerador de partículas requieren la criogenización de ciertos circuitos para conseguir superconductores. Esto es posible gracias a la combinación de compresores de [[helio]] alimentados con [[nitrógeno líquido]], el cual entra a los circuitos aproximadamente a {{esd|80 K}} ({{esd|−193.15 °C}}) para ir bajando de temperatura en su transcurso por el circuito de los tres compresores.<ref name="cern">{{cita web |
||
| url = http://cdsweb.cern.ch/record/834142 |
| url = http://cdsweb.cern.ch/record/834142 |
||
| título = CERN Document Server: Record#834142: LHC: A cool 1.8 K is achieved for the first time |
| título = CERN Document Server: Record#834142: LHC: A cool 1.8 K is achieved for the first time |
||
}}<!--Título generado por Muro Bot--></ref> La temperatura más baja alcanzada en el LHC es de 1 |
}}<!--Título generado por Muro Bot--></ref> La temperatura más baja alcanzada en el LHC es de 1.8 K.<ref name="cern" /> |
||
==Temperaturas negativas== |
|||
{{Main|Temperatura negativa}} |
|||
Las temperaturas que se expresan como números negativos en las conocidas escalas Celsius o Fahrenheit son simplemente más frías que los puntos cero de dichas escalas. Ciertos [[Sistemas termodinámicos|sistemas]] pueden alcanzar temperaturas verdaderamente negativas; es decir, su [[Temperatura termodinámica]] (expresada en kelvins) puede ser de una cantidad [[Número negativo|negativa]]. Un sistema con una temperatura realmente negativa no es más frío que el cero absoluto. Más bien, un sistema con una temperatura negativa es más caliente que ''cualquier'' sistema con una temperatura positiva, en el sentido de que si un sistema de temperatura negativa y un sistema de temperatura positiva entran en contacto, el calor fluye del sistema negativo al sistema de temperatura positiva.<ref name="Chase">{{cite web|last=Chase|first=Scott|title=Bajo el cero absoluto -¿Qué significa temperatura negativa? |url=http://www.phys.ncku.edu.tw/mirrors/physicsfaq/ParticleAndNuclear/neg_temperature.html|work=The Physics and Relativity FAQ|access-date=2 de julio de 2010|archive-url=https://web.archive.org/web/20110815144418/http://www.phys.ncku.edu.tw/mirrors/physicsfaq/ParticleAndNuclear/neg_temperature.html|archive-date=15 de agosto de 2011|url-status=}}</ref> |
|||
La mayoría de los sistemas conocidos no pueden alcanzar temperaturas negativas porque la adición de energía siempre aumenta su [[entropía]]. Sin embargo, algunos sistemas tienen una cantidad máxima de energía que pueden mantener, y a medida que se acercan a esa energía máxima su entropía comienza a disminuir. Debido a que la temperatura se define por la relación entre la energía y la entropía, la temperatura de un sistema de este tipo se vuelve negativa, a pesar de que se está añadiendo energía.<ref name="Chase"/> Como resultado, el factor de Boltzmann para los estados de los sistemas a temperatura negativa aumenta en lugar de disminuir con el aumento de la energía del estado. Por lo tanto, ningún sistema completo, es decir, incluyendo los modos electromagnéticos, puede tener temperaturas negativas, ya que no existe el estado de mayor energía,{{citation needed|date=octubre 2016}} de modo que la suma de las probabilidades de los estados divergiría para temperaturas negativas. Sin embargo, para sistemas de cuasi-equilibrio (por ejemplo, espines fuera de equilibrio con el campo electromagnético) este argumento no se aplica, y las temperaturas efectivas negativas son alcanzables. |
|||
El 3 de enero de 2013, los físicos anunciaron que por primera vez habían creado un gas cuántico formado por átomos de potasio con una temperatura negativa en grados de libertad de movimiento.<ref>{{cite journal|doi=10.1038/nature.2013.12146|title=El gas cuántico desciende por debajo del cero absoluto|journal=Nature|year=2013|last1=Merali|first1=Zeeya|s2cid=124101032|doi-access=}}</ref> |
|||
== Termodinámica cerca del cero absoluto == |
|||
A temperaturas cercanas a {{esd|0 K}} ({{esd|−273.15 °C}}; {{esd|−459.67 °F}}) cesa casi todo movimiento molecular y {{esd|Δ''S'' = 0}} para cualquier [[proceso adiabático]], donde ''S'' es la [[entropía]]. En tales circunstancias, las sustancias puras pueden (idealmente) formar cristales perfectos sin imperfecciones estructurales cuando {{esd|''T'' → 0}}. La forma fuerte de [[Max Planck]] de la [[tercera ley de la termodinámica]] establece que la entropía de un cristal perfecto desaparece en el cero absoluto. El original [[Walther Nernst|Nernst]] ''[[teorema del calor de Nernst|teorema del calor]]'' hace la afirmación más débil y menos controvertida de que el cambio de entropía para cualquier [[proceso isotérmico]] se aproxima a cero a medida que {{esd|''T'' → 0}}: |
|||
:<math> \lim_{T \to 0} \Delta S = 0 </math> |
|||
La implicación es que la entropía de un cristal perfecto se aproxima a un valor constante. Un adiabato es un estado con entropía constante, típicamente representado en un gráfico como una curva de manera similar a las isotermas e isobaras. |
|||
<blockquote>La [[Tercera ley de la termodinámica|Postulado de Nernst]] identifica la [[proceso isotérmico|isoterma]] {{esd|T = 0}} como coincidente con la [[Adiabático|adiabática]] {{esd|S = 0}}, aunque otras isotermas y adiabats son distintos. Como no hay dos adiabáticas que se crucen, ningúna otra adiabática puede [[Intersección de dos rectas|intersecar]] la isoterma {{esd|T = 0}}. En consecuencia, ningún proceso adiabático iniciado a temperatura distinta de cero puede conducir a temperatura cero. (≈ Callen, pp. 189‑190)</blockquote> |
|||
Un cristal perfecto es aquel en el que la estructura interna [[red (grupo)|red]] se extiende ininterrumpidamente en todas las direcciones. El orden perfecto puede representarse por [[simetría]] traslacional a lo largo de tres (no suelen ser [[Ortogonalidad (matemática)|ortogonales]]) [[sistema de coordenadas cartesianas|ejes]]. Cada elemento reticular de la estructura se encuentra en el lugar que le corresponde, tanto si se trata de un átomo individual como de una agrupación molecular. Para [[sustancia química|sustancias]] que existen en dos (o más) formas cristalinas estables, como el diamante y el [[grafito]] para el [[carbono]], existe una especie de ''degeneración química''. La cuestión sigue siendo si ambos pueden tener entropía cero a {{esd|''T'' = 0}} aunque cada uno esté perfectamente ordenado. |
|||
Los cristales perfectos nunca se dan en la práctica; las imperfecciones, e incluso inclusiones enteras de material amorfo, pueden «congelarse» a bajas temperaturas, y de hecho lo hacen, por lo que no se producen transiciones a estados más estables. |
|||
Utilizando el [[modelo de Debye]], la [[capacidad calorífica específica|calor específico]] y la entropía de un cristal puro son proporcionales a {{esd|''T'' <sup>3</sup>}}, mientras que la [[entalpía]] y el [[potencial químico]] son proporcionales a {{esd|''T'' <sup>4</sup>}}. (Guggenheim, p. 111) Estas cantidades caen hacia sus valores límite de {{esd|''T'' = 0}} y se aproximan con pendientes ''cero''. Al menos para los calores específicos, el propio valor límite es definitivamente cero, como lo confirman los experimentos por debajo de {{esd|10 K}}. Incluso el menos detallado [[sólido de Einstein|modelo de Einstein]] muestra esta curiosa caída en los calores específicos. De hecho, todos los calores específicos desaparecen en el cero absoluto, no sólo los de los cristales. Lo mismo ocurre con el coeficiente de [[dilatación térmica]]. Las [[relaciones de Maxwell]] muestran que otras magnitudes también desaparecen. Estos fenómenos no estaban previstos. |
|||
Dado que la relación entre los cambios en la [[energía libre de Gibbs]] (''G''), la entalpía (''H'') y la entropía es |
|||
:<math> \Delta G = \Delta H - T \Delta S \,</math> |
|||
Así, a medida que ''T'' disminuye, Δ''G'' y Δ''H'' se aproximan (siempre que Δ''S'' esté acotado). Experimentalmente, se encuentra que todos los procesos espontáneos (incluyendo [[reacción química]]) resultan en una disminución de ''G'' a medida que avanzan hacia el [[equilibrio termodinámico|equilibrio]]. Si Δ''S'' y/o ''T'' son pequeños, la condición {{esd|Δ''G'' < 0}} puede implicar que {{esd|Δ''H''< 0}}, lo que indicaría una reacción [[exotérmica]]. Sin embargo, esto no es necesario; las reacciones [[Proceso endotérmico| endotérmicas]] pueden proceder espontáneamente si el término ''T''Δ''S'' es suficientemente grande. |
|||
Además, las pendientes de las [[derivadas]] de Δ''G'' y Δ''H'' convergen y son iguales a cero en {{esd|''T'' = 0}}. Esto asegura que Δ''G'' y Δ''H'' son casi iguales en un rango considerable de temperaturas y justifica el [[empirismo|empírico]] aproximado. Principio de Thomsen y Berthelot, que afirma que ''el estado de equilibrio al que procede un sistema es el que evoluciona la mayor cantidad de calor'', es decir, un proceso real es el ''más exotérmico''. (Callen, pp. 186‑187) |
|||
Un modelo que estima las propiedades de un [[electrón]] gaseoso en el cero absoluto de los metales es el [[gas de Fermi]]. Los electrones, al ser [[fermiones]]s, deben estar en diferentes estados cuánticos, lo que lleva a los electrones a obtener velocidades típicas muy altas, incluso en el cero absoluto. La energía máxima que pueden tener los electrones en el cero absoluto se denomina [[energía de Fermi]]. La temperatura de Fermi se define como esta energía máxima dividida por la constante de Boltzmann, y es del orden de {{esd|80 000 K}} para las densidades típicas de electrones que se encuentran en los metales. Para temperaturas significativamente inferiores a la temperatura de Fermi, los electrones se comportan prácticamente igual que en el cero absoluto. Esto explica el fracaso del [[teorema de equipartición]] clásico para los metales que eludió a los físicos clásicos a finales del {{siglo|XIX||s}}. |
|||
== Historia == |
== Historia == |
||
[[Archivo:Robert Boyle 0001.jpg|thumb|right|[[Robert Boyle]] fue pionero en la idea de un cero absoluto.]] |
[[Archivo:Robert Boyle 0001.jpg|thumb|right|[[Robert Boyle]] fue pionero en la idea de un cero absoluto.]] |
||
Uno de los primeros científicos que discutió la posibilidad de una temperatura mínima absoluta fue [[Robert Boyle]]. Su texto de 1665 ''New Experiments and Observations touching Cold'' (''[[Nuevos experimentos y observaciones acerca del cero absoluto ]]''), articula la disputa conocida como el ''primum frigidum''.<ref>{{cita libro|url=http://books.google.com/books?id=8vRaAAAAMAAJ&pg=PA651|título=The Stanford Dictionary of Anglicised Words and Phrases|autor=Stanford, John Frederick|año=1892 }}</ref> El concepto era bien conocido entre los naturalistas de la época. Algunos sostenían que esa temperatura mínima absoluta se producía dentro de la Tierra (dado que era uno de los llamados cuatro «elementos»), otros que dentro del agua y otros que en el aire, y algunos más recientemente en el [[nitro (mineral)|nitro]]. Aunque todos ellos parecían estar de acuerdo en que: «Hay un cuerpo u otro que por su propia naturaleza es sumamente frío y que por su participación todos los demás cuerpos obtienen esa calidad».<ref> |
Uno de los primeros científicos que discutió la posibilidad de una temperatura mínima absoluta fue [[Robert Boyle]]. Su texto de 1665 ''New Experiments and Observations touching Cold'' (''[[Nuevos experimentos y observaciones acerca del cero absoluto ]]''), articula la disputa conocida como el ''primum frigidum''.<ref>{{cita libro|url=http://books.google.com/books?id=8vRaAAAAMAAJ&pg=PA651|título=The Stanford Dictionary of Anglicised Words and Phrases|autor=Stanford, John Frederick|año=1892 }}</ref> El concepto era bien conocido entre los naturalistas de la época. Algunos sostenían que esa temperatura mínima absoluta se producía dentro de la Tierra (dado que era uno de los llamados cuatro «elementos»), otros que dentro del agua y otros que en el aire, y algunos más recientemente en el [[nitro (mineral)|nitro]]. Aunque todos ellos parecían estar de acuerdo en que: «Hay un cuerpo u otro que por su propia naturaleza es sumamente frío y que por su participación todos los demás cuerpos obtienen esa calidad».<ref>«There is some body or other that is of its own nature supremely cold and by participation of which all other bodies obtain that quality». {{cita libro|apellido=Boyle|nombre=Robert|título=New Experiments and Observations touching Cold|url=https://archive.org/details/b30334457|año=1665}}</ref> |
||
=== Límite para el «grado de frío» === |
=== Límite para el «grado de frío» === |
||
La cuestión de si existía un límite para el grado de frío posible y, si así fuese, dónde se debía colocar el cero, fue abordada por primera vez por el físico francés [[Guillaume Amontons]] en 1702, en relación con su mejoras en el [[termómetro de gas|termómetro de aire]]. En su instrumento, las temperaturas estaban indicadas por la altura a la que era sostenida una columna de mercurio por una determinada masa de aire, el volumen, o «primavera», que variaba con el calor a la que estuviera expuesta. Por ello Amontons argumentó que el cero de su termómetro sería la temperatura a la cual el volumen del aire en él se redujese a nada. En la escala que utilizó, el punto de ebullición del agua se marcó en +73 y el punto de fusión del hielo a los 51, por lo que el cero de su escala era equivalente a alrededor de −240 |
La cuestión de si existía un límite para el grado de frío posible y, si así fuese, dónde se debía colocar el cero, fue abordada por primera vez por el físico francés [[Guillaume Amontons]] en 1702, en relación con su mejoras en el [[termómetro de gas|termómetro de aire]]. En su instrumento, las temperaturas estaban indicadas por la altura a la que era sostenida una columna de mercurio por una determinada masa de aire, el volumen, o «primavera», que variaba con el calor a la que estuviera expuesta. Por ello Amontons argumentó que el cero de su termómetro sería la temperatura a la cual el volumen del aire en él se redujese a nada. En la escala que utilizó, el punto de ebullición del agua se marcó en +73 y el punto de fusión del hielo a los 51, por lo que el cero de su escala era equivalente a alrededor de {{esd|−240 °C}}.{{citation needed|date=November 2011}} |
||
Esta aproximación al valor moderno de {{ |
Esta aproximación al valor moderno de {{esd|−273.15 °C}} del cero del termómetro de aire fue mejorada ulteriormente en 1779 por [[Johann Heinrich Lambert]], quien observó que {{esd|−270 °C}} podría considerarse como el frío absoluto.<ref>{{cita libro|apellido=Lambert|nombre=Johann Heinrich|título=Pyrometrie|ubicación=Berlin|año=1779|oclc=165756016}}</ref> |
||
Los valores de este orden para el cero absoluto no eran, sin embargo, universalmente aceptados en la época. [[Pierre-Simon Laplace]] y [[Antoine Lavoisier]], en su tratado sobre el calor de 1780, llegaron a valores que iban de 1500 a 3000 por debajo del punto de congelación del agua, y pensaron que, en cualquier caso, debía ser, por lo menos, de 600 menos. [[John Dalton]] en su ''Chemical Philosophy'' dio diez cálculos de este valor, y finalmente adoptó {{ |
Los valores de este orden para el cero absoluto no eran, sin embargo, universalmente aceptados en la época. [[Pierre-Simon Laplace]] y [[Antoine Lavoisier]], en su tratado sobre el calor de 1780, llegaron a valores que iban de 1500 a 3000 por debajo del punto de congelación del agua, y pensaron que, en cualquier caso, debía ser, por lo menos, de 600 menos. [[John Dalton]] en su ''Chemical Philosophy'' dio diez cálculos de este valor, y finalmente adoptó {{esd|−3000 °C}} como el cero natural de la temperatura. |
||
=== Trabajo de Lord Kelvin === |
=== Trabajo de Lord Kelvin === |
||
Después de que [[James Prescott Joule]] hubiese determinado el [[equivalente mecánico del calor]], [[Lord Kelvin]] abordó la cuestión desde un punto de vista totalmente diferente, y, en 1848, ideó una escala de temperatura absoluta, que era independiente de las propiedades de cualquier sustancia en particular y se basaba únicamente en los [[principios de la termodinámica|principios fundamentales de la termodinámica]]. Partiendo de los axiomas de esa escala, situó su cero en {{ |
Después de que [[James Prescott Joule]] hubiese determinado el [[equivalente mecánico del calor]], [[Lord Kelvin]] abordó la cuestión desde un punto de vista totalmente diferente, y, en 1848, ideó una escala de temperatura absoluta, que era independiente de las propiedades de cualquier sustancia en particular y se basaba únicamente en los [[principios de la termodinámica|principios fundamentales de la termodinámica]]. Partiendo de los axiomas de esa escala, situó su cero en {{esd|−273.15 °C}}, en casi exactamente el mismo punto que el cero del termómetro de aire.<ref>{{Cita enciclopedia|enciclopedia=Encyclopædia Britannica|título=Cold|url=http://www.1911encyclopedia.org/Cold|fechaacceso=11 de febrero de 2008|edición= Undécima|año=1911|editorial=The LoveToKnow Wiki|urlarchivo=https://web.archive.org/web/20071212195823/http://www.1911encyclopedia.org/Cold|fechaarchivo=12 de diciembre de 2007}}</ref> |
||
=== Ley de Charles === |
|||
De 1787 a 1802, fue determinada por [[Jacques Charles]], [[John Dalton]],<ref>J. Dalton (1802), [https://books.google.com/books?id=3qdJAAAAYAAJ&pg=PA595 «Ensayo II. Sobre la fuerza del vapor de agua y de otros líquidos diversos, tanto en el vacío como en el aire» y «Ensayo IV. Sobre la expansión de los fluidos elásticos por el calor», ] ''Memorias de la Sociedad Literaria y Filosófica de Manchester'', vol. 8, pt. 2, pp. 550-74, 595-602.</ref> y [[Joseph Louis Gay-Lussac]]<ref>{{citation |author=Gay-Lussac, J. L. |author-link=Joseph Louis Gay-Lussac |year=1802 |title=Recherches sur la dilatation des gaz et des vapeurs |journal=Annales de Chimie |volume=XLIII |page=137}}. [http://web.lemoyne.edu/~giunta/gaygas.html Traducción al español (extracto).]</ref> que, a presión constante, los gases ideales expandían o contraían su volumen linealmente ([[ley de Charles]]) en aproximadamente 1/273 partes por grado Celsius de cambio de temperatura hacia arriba o hacia abajo, entre 0° y {{esd|100 °C}}. Esto sugería que el volumen de un gas enfriado a unos {{esd|−273 °C}} llegaría a cero. |
|||
===La carrera hacia el cero absoluto=== |
|||
{{véase también|Anexo:Cronología de la tecnología de bajas temperaturas}} |
|||
[[Archivo:Leiden - Kamerlingh Onnes Building - Commemorative plaque.jpg|thumb|Placa conmemorativa en Leiden]] |
|||
Con una mejor comprensión teórica del cero absoluto, los científicos estaban ansiosos por alcanzar esta temperatura en el laboratorio.<ref name="MyUser_YouTube_November_23_2016c">{{cite web |url=https://www.youtube.com/watch?v=mTFRgosx4aQ&t=894s |archive-url=https://web.archive.org/web/20170406015107/https://www.youtube.com/watch |archive-date=6 de abril de 2017 |url-status= |title=ABSOLUTO CERO - DOCUMENTAL DE PBS NOVA (completo) |newspaper=YouTube |access-date=23 de noviembre de 2016 |deadurl=no }}</ref> En 1845, [[Michael Faraday]] había conseguido licuar la mayoría de los gases que se conocían entonces, y alcanzó un nuevo récord de temperaturas más bajas al llegar a −130 grados Celsius ({{esd|−202.0 °F}}; {{esd|143.2 K}}). Faraday creía que ciertos gases, como el oxígeno, el nitrógeno y el [[hidrógeno]], eran gases permanentes y no podían licuarse.<ref>[http://www.scienceclarified.com/Co-Di/Cryogenics.html Cryogenics]. Scienceclarified.com. Recuperado el 22 de julio de 2012.</ref> Décadas más tarde, en 1873 el científico teórico neerlandés [[Johannes Diderik van der Waals]] demostró que estos gases podían licuarse, pero solo en condiciones de presión muy alta y temperaturas muy bajas. En 1877, [[Louis Paul Cailletet]] en Francia y [[Raoul Pictet]] en Suiza consiguieron producir las primeras gotas de [[aire líquido]] a −195 grados Celsius ({{esd|−319.0 °F}}; {{esd|78.2 K}}). A continuación, en 1883, los profesores polacos [[Zygmunt Wróblewski]] y [[Karol Olszewski]] produjeron oxígeno líquido −218 grados Celsius ({{esd|−360.4 °F}}; {{esd|55.2 K}}). |
|||
El químico y físico escocés [[James Dewar]] y el físico neerlandés [[Heike Kamerlingh Onnes]] aceptaron el reto de licuar los gases restantes, hidrógeno y [[helio]]. En 1898, tras 20 años de esfuerzos, Dewar fue el primero en licuar el hidrógeno, alcanzando un nuevo récord de baja temperatura de −252 grados Celsius ({{esd|−421.6 °F}}; {{esd|21.2 K}}). Sin embargo, Kamerlingh Onnes, su rival, fue el primero en licuar helio, en 1908, utilizando varias etapas de preenfriamiento y el [[Sistema de Linde-Hampson| ciclo Hampson-Linde]]. Bajó la temperatura hasta el punto de ebullición del helio −269 grados Celsius ({{esd|−452.2 °F}}; {{esd|4.2 K}}). Al reducir la presión del helio líquido consiguió una temperatura aún más baja, cercana a 1.5 K. Éstas fueron las [[Temperaturas más bajas registradas en la Tierra|temperaturas más frías alcanzadas en la Tierra]] de la época y su logro le valió el [[Premio Nobel]] en 1913.<ref name="nobel">{{cite web|url=https://www.nobelprize.org/nobel_prizes/physics/laureates/1913/onnes-bio.html|title=El Premio Nobel de Física 1913: Heike Kamerlingh Onnes|publisher=Nobel Media AB|access-date=24 de abril de 2012}}</ref> Kamerlingh Onnes continuaría estudiando las propiedades de los materiales a temperaturas cercanas al cero absoluto, describiendo por primera vez la [[superconductividad]] y los [[superfluidos]]. |
|||
== Véase también == |
== Véase también == |
||
Revisión actual - 16:32 4 dic 2024
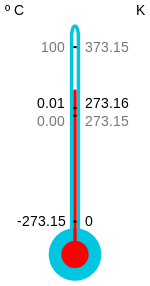
El cero absoluto es la temperatura más baja posible. A esta temperatura el nivel de energía interna del sistema es el más bajo posible, por lo que las moléculas, según la mecánica clásica, carecen de movimiento;[1] no obstante, según la mecánica cuántica, el cero absoluto debe tener una energía residual, llamada energía de punto cero, para poder así cumplir el principio de indeterminación de Heisenberg. El cero absoluto sirve de punto de partida tanto para la escala de Kelvin como para la escala de Rankine.[2] Así, 0 K (o lo que es lo mismo, 0 R) corresponden, por definición según acuerdo internacional, a la temperatura de −273.15 °C o −459.67 °F.[3]
Según el tercer principio de la termodinámica, el cero absoluto es un límite inalcanzable. En septiembre de 2014, los científicos de la colaboración CUORE en el Laboratori Nazionali del Gran Sasso en Italia enfriaron un recipiente de cobre con un volumen de un metro cúbico a 0.006 K (−273.144 °C) durante 15 días, estableciendo un récord para la temperatura más baja registrada en el universo conocido sobre un volumen contiguo tan grande. La dificultad para llegar a una temperatura tan baja en una cámara de enfriamiento es el hecho que las moléculas de la cámara, al llegar a esa temperatura, no tienen energía suficiente para hacer que esta descienda aún más.
La entropía de un cristal ideal puro y perfecto sería cero. Si los átomos que lo componen no forman un cristal perfecto, su entropía debe ser mayor que cero, por lo que la temperatura siempre será superior al cero absoluto y el cristal siempre tendrá imperfecciones inducidas por el movimiento de sus átomos, necesitando un movimiento que lo compense y, por lo tanto, teniendo siempre una imperfección residual.
Cabe mencionar que a 0 K absolutamente todas las sustancias conocidas se solidificarían y que según el actual modelo del calor, las moléculas perderían toda capacidad de moverse, vibrar o rotar.

Hasta ahora la temperatura más cercana al cero absoluto ha sido obtenida en laboratorio por científicos del Instituto Tecnológico de Massachusetts en junio del 2015. Se obtuvo enfriando un gas en un campo magnético hasta 500 nK (5 × 10−7 K) por encima del cero absoluto.[4]
Fenómenos cerca del cero absoluto
[editar]
Al aproximarse al cero absoluto se pueden producir en algunos materiales ciertos fenómenos, como el condensado de Bose-Einstein, o algunos superfluidos como el helio II.
En 1924, Albert Einstein y el físico indio Satyendranath Bose predijeron la existencia de un fenómeno denominado condensado de Bose-Einstein. En dicho estado, los bosones se agrupan en el mismo estado cuántico de energía. Este fenómeno se confirmó en 1995, y desde entonces se han investigado muchas de sus propiedades.
A temperaturas muy próximas al cero absoluto se pueden formar superfluidos, o incluso frágiles moléculas que no existen a mayores temperaturas para su estudio, entre otros fenómenos.
En la actualidad se puede encontrar una aplicación práctica en el acelerador de partículas LHC del CERN.[5] El Gran Colisionador de Hadrones (LHC) alcanza una temperatura de 1.9 K. Los experimentos que se llevarán a cabo en este acelerador de partículas requieren la criogenización de ciertos circuitos para conseguir superconductores. Esto es posible gracias a la combinación de compresores de helio alimentados con nitrógeno líquido, el cual entra a los circuitos aproximadamente a 80 K (−193.15 °C) para ir bajando de temperatura en su transcurso por el circuito de los tres compresores.[6] La temperatura más baja alcanzada en el LHC es de 1.8 K.[6]
Temperaturas negativas
[editar]Las temperaturas que se expresan como números negativos en las conocidas escalas Celsius o Fahrenheit son simplemente más frías que los puntos cero de dichas escalas. Ciertos sistemas pueden alcanzar temperaturas verdaderamente negativas; es decir, su Temperatura termodinámica (expresada en kelvins) puede ser de una cantidad negativa. Un sistema con una temperatura realmente negativa no es más frío que el cero absoluto. Más bien, un sistema con una temperatura negativa es más caliente que cualquier sistema con una temperatura positiva, en el sentido de que si un sistema de temperatura negativa y un sistema de temperatura positiva entran en contacto, el calor fluye del sistema negativo al sistema de temperatura positiva.[7]
La mayoría de los sistemas conocidos no pueden alcanzar temperaturas negativas porque la adición de energía siempre aumenta su entropía. Sin embargo, algunos sistemas tienen una cantidad máxima de energía que pueden mantener, y a medida que se acercan a esa energía máxima su entropía comienza a disminuir. Debido a que la temperatura se define por la relación entre la energía y la entropía, la temperatura de un sistema de este tipo se vuelve negativa, a pesar de que se está añadiendo energía.[7] Como resultado, el factor de Boltzmann para los estados de los sistemas a temperatura negativa aumenta en lugar de disminuir con el aumento de la energía del estado. Por lo tanto, ningún sistema completo, es decir, incluyendo los modos electromagnéticos, puede tener temperaturas negativas, ya que no existe el estado de mayor energía,[cita requerida] de modo que la suma de las probabilidades de los estados divergiría para temperaturas negativas. Sin embargo, para sistemas de cuasi-equilibrio (por ejemplo, espines fuera de equilibrio con el campo electromagnético) este argumento no se aplica, y las temperaturas efectivas negativas son alcanzables.
El 3 de enero de 2013, los físicos anunciaron que por primera vez habían creado un gas cuántico formado por átomos de potasio con una temperatura negativa en grados de libertad de movimiento.[8]
Termodinámica cerca del cero absoluto
[editar]A temperaturas cercanas a 0 K (−273.15 °C; −459.67 °F) cesa casi todo movimiento molecular y para cualquier proceso adiabático, donde S es la entropía. En tales circunstancias, las sustancias puras pueden (idealmente) formar cristales perfectos sin imperfecciones estructurales cuando T → 0. La forma fuerte de Max Planck de la tercera ley de la termodinámica establece que la entropía de un cristal perfecto desaparece en el cero absoluto. El original Nernst teorema del calor hace la afirmación más débil y menos controvertida de que el cambio de entropía para cualquier proceso isotérmico se aproxima a cero a medida que T → 0:
La implicación es que la entropía de un cristal perfecto se aproxima a un valor constante. Un adiabato es un estado con entropía constante, típicamente representado en un gráfico como una curva de manera similar a las isotermas e isobaras.
La Postulado de Nernst identifica la isoterma como coincidente con la adiabática , aunque otras isotermas y adiabats son distintos. Como no hay dos adiabáticas que se crucen, ningúna otra adiabática puede intersecar la isoterma . En consecuencia, ningún proceso adiabático iniciado a temperatura distinta de cero puede conducir a temperatura cero. (≈ Callen, pp. 189‑190)
Un cristal perfecto es aquel en el que la estructura interna red se extiende ininterrumpidamente en todas las direcciones. El orden perfecto puede representarse por simetría traslacional a lo largo de tres (no suelen ser ortogonales) ejes. Cada elemento reticular de la estructura se encuentra en el lugar que le corresponde, tanto si se trata de un átomo individual como de una agrupación molecular. Para sustancias que existen en dos (o más) formas cristalinas estables, como el diamante y el grafito para el carbono, existe una especie de degeneración química. La cuestión sigue siendo si ambos pueden tener entropía cero a aunque cada uno esté perfectamente ordenado.
Los cristales perfectos nunca se dan en la práctica; las imperfecciones, e incluso inclusiones enteras de material amorfo, pueden «congelarse» a bajas temperaturas, y de hecho lo hacen, por lo que no se producen transiciones a estados más estables.
Utilizando el modelo de Debye, la calor específico y la entropía de un cristal puro son proporcionales a T 3, mientras que la entalpía y el potencial químico son proporcionales a T 4. (Guggenheim, p. 111) Estas cantidades caen hacia sus valores límite de y se aproximan con pendientes cero. Al menos para los calores específicos, el propio valor límite es definitivamente cero, como lo confirman los experimentos por debajo de 10 K. Incluso el menos detallado modelo de Einstein muestra esta curiosa caída en los calores específicos. De hecho, todos los calores específicos desaparecen en el cero absoluto, no sólo los de los cristales. Lo mismo ocurre con el coeficiente de dilatación térmica. Las relaciones de Maxwell muestran que otras magnitudes también desaparecen. Estos fenómenos no estaban previstos.
Dado que la relación entre los cambios en la energía libre de Gibbs (G), la entalpía (H) y la entropía es
Así, a medida que T disminuye, ΔG y ΔH se aproximan (siempre que ΔS esté acotado). Experimentalmente, se encuentra que todos los procesos espontáneos (incluyendo reacción química) resultan en una disminución de G a medida que avanzan hacia el equilibrio. Si ΔS y/o T son pequeños, la condición ΔG < 0 puede implicar que ΔH< 0, lo que indicaría una reacción exotérmica. Sin embargo, esto no es necesario; las reacciones endotérmicas pueden proceder espontáneamente si el término TΔS es suficientemente grande.
Además, las pendientes de las derivadas de ΔG y ΔH convergen y son iguales a cero en . Esto asegura que ΔG y ΔH son casi iguales en un rango considerable de temperaturas y justifica el empírico aproximado. Principio de Thomsen y Berthelot, que afirma que el estado de equilibrio al que procede un sistema es el que evoluciona la mayor cantidad de calor, es decir, un proceso real es el más exotérmico. (Callen, pp. 186‑187)
Un modelo que estima las propiedades de un electrón gaseoso en el cero absoluto de los metales es el gas de Fermi. Los electrones, al ser fermioness, deben estar en diferentes estados cuánticos, lo que lleva a los electrones a obtener velocidades típicas muy altas, incluso en el cero absoluto. La energía máxima que pueden tener los electrones en el cero absoluto se denomina energía de Fermi. La temperatura de Fermi se define como esta energía máxima dividida por la constante de Boltzmann, y es del orden de 80 000 K para las densidades típicas de electrones que se encuentran en los metales. Para temperaturas significativamente inferiores a la temperatura de Fermi, los electrones se comportan prácticamente igual que en el cero absoluto. Esto explica el fracaso del teorema de equipartición clásico para los metales que eludió a los físicos clásicos a finales del siglo XIX.
Historia
[editar]
Uno de los primeros científicos que discutió la posibilidad de una temperatura mínima absoluta fue Robert Boyle. Su texto de 1665 New Experiments and Observations touching Cold (Nuevos experimentos y observaciones acerca del cero absoluto ), articula la disputa conocida como el primum frigidum.[9] El concepto era bien conocido entre los naturalistas de la época. Algunos sostenían que esa temperatura mínima absoluta se producía dentro de la Tierra (dado que era uno de los llamados cuatro «elementos»), otros que dentro del agua y otros que en el aire, y algunos más recientemente en el nitro. Aunque todos ellos parecían estar de acuerdo en que: «Hay un cuerpo u otro que por su propia naturaleza es sumamente frío y que por su participación todos los demás cuerpos obtienen esa calidad».[10]
Límite para el «grado de frío»
[editar]La cuestión de si existía un límite para el grado de frío posible y, si así fuese, dónde se debía colocar el cero, fue abordada por primera vez por el físico francés Guillaume Amontons en 1702, en relación con su mejoras en el termómetro de aire. En su instrumento, las temperaturas estaban indicadas por la altura a la que era sostenida una columna de mercurio por una determinada masa de aire, el volumen, o «primavera», que variaba con el calor a la que estuviera expuesta. Por ello Amontons argumentó que el cero de su termómetro sería la temperatura a la cual el volumen del aire en él se redujese a nada. En la escala que utilizó, el punto de ebullición del agua se marcó en +73 y el punto de fusión del hielo a los 51, por lo que el cero de su escala era equivalente a alrededor de −240 °C.[cita requerida]
Esta aproximación al valor moderno de −273.15 °C del cero del termómetro de aire fue mejorada ulteriormente en 1779 por Johann Heinrich Lambert, quien observó que −270 °C podría considerarse como el frío absoluto.[11]
Los valores de este orden para el cero absoluto no eran, sin embargo, universalmente aceptados en la época. Pierre-Simon Laplace y Antoine Lavoisier, en su tratado sobre el calor de 1780, llegaron a valores que iban de 1500 a 3000 por debajo del punto de congelación del agua, y pensaron que, en cualquier caso, debía ser, por lo menos, de 600 menos. John Dalton en su Chemical Philosophy dio diez cálculos de este valor, y finalmente adoptó −3000 °C como el cero natural de la temperatura.
Trabajo de Lord Kelvin
[editar]Después de que James Prescott Joule hubiese determinado el equivalente mecánico del calor, Lord Kelvin abordó la cuestión desde un punto de vista totalmente diferente, y, en 1848, ideó una escala de temperatura absoluta, que era independiente de las propiedades de cualquier sustancia en particular y se basaba únicamente en los principios fundamentales de la termodinámica. Partiendo de los axiomas de esa escala, situó su cero en −273.15 °C, en casi exactamente el mismo punto que el cero del termómetro de aire.[12]
Ley de Charles
[editar]De 1787 a 1802, fue determinada por Jacques Charles, John Dalton,[13] y Joseph Louis Gay-Lussac[14] que, a presión constante, los gases ideales expandían o contraían su volumen linealmente (ley de Charles) en aproximadamente 1/273 partes por grado Celsius de cambio de temperatura hacia arriba o hacia abajo, entre 0° y 100 °C. Esto sugería que el volumen de un gas enfriado a unos −273 °C llegaría a cero.
La carrera hacia el cero absoluto
[editar]
Con una mejor comprensión teórica del cero absoluto, los científicos estaban ansiosos por alcanzar esta temperatura en el laboratorio.[15] En 1845, Michael Faraday había conseguido licuar la mayoría de los gases que se conocían entonces, y alcanzó un nuevo récord de temperaturas más bajas al llegar a −130 grados Celsius (−202.0 °F; 143.2 K). Faraday creía que ciertos gases, como el oxígeno, el nitrógeno y el hidrógeno, eran gases permanentes y no podían licuarse.[16] Décadas más tarde, en 1873 el científico teórico neerlandés Johannes Diderik van der Waals demostró que estos gases podían licuarse, pero solo en condiciones de presión muy alta y temperaturas muy bajas. En 1877, Louis Paul Cailletet en Francia y Raoul Pictet en Suiza consiguieron producir las primeras gotas de aire líquido a −195 grados Celsius (−319.0 °F; 78.2 K). A continuación, en 1883, los profesores polacos Zygmunt Wróblewski y Karol Olszewski produjeron oxígeno líquido −218 grados Celsius (−360.4 °F; 55.2 K).
El químico y físico escocés James Dewar y el físico neerlandés Heike Kamerlingh Onnes aceptaron el reto de licuar los gases restantes, hidrógeno y helio. En 1898, tras 20 años de esfuerzos, Dewar fue el primero en licuar el hidrógeno, alcanzando un nuevo récord de baja temperatura de −252 grados Celsius (−421.6 °F; 21.2 K). Sin embargo, Kamerlingh Onnes, su rival, fue el primero en licuar helio, en 1908, utilizando varias etapas de preenfriamiento y el ciclo Hampson-Linde. Bajó la temperatura hasta el punto de ebullición del helio −269 grados Celsius (−452.2 °F; 4.2 K). Al reducir la presión del helio líquido consiguió una temperatura aún más baja, cercana a 1.5 K. Éstas fueron las temperaturas más frías alcanzadas en la Tierra de la época y su logro le valió el Premio Nobel en 1913.[17] Kamerlingh Onnes continuaría estudiando las propiedades de los materiales a temperaturas cercanas al cero absoluto, describiendo por primera vez la superconductividad y los superfluidos.
Véase también
[editar]Referencias
[editar]- ↑ Pierre J. Rapin – Prontuario del frío, p. 5, en Google Libros
- ↑ von Reichenbach, María Cecilia; Bergero, Paula Elena; Álvarez, Ariel; del Río, Laura. Reichenbach, María Cecilia von, ed. Cero absoluto. Curiosidades de física. Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET). p. 104. ISBN 978-950-692-088-3.
- ↑ Jerry D. Wilson, Anthony J Buffa – Física, p. 354, en Google Libros
- ↑ «MIT team creates ultracold molecules». Massachusetts Institute of Technology, Massachusetts, Cambridge. Archivado desde el original el 18 de agosto de 2015. Consultado el 2 de octubre de 2019.
- ↑ «CERN Bulletin».
- ↑ a b «CERN Document Server: Record#834142: LHC: A cool 1.8 K is achieved for the first time».
- ↑ a b Chase, Scott. «Bajo el cero absoluto -¿Qué significa temperatura negativa?». The Physics and Relativity FAQ. Archivado desde el original el 15 de agosto de 2011. Consultado el 2 de julio de 2010.
- ↑ Merali, Zeeya (2013). «El gas cuántico desciende por debajo del cero absoluto». Nature. S2CID 124101032. doi:10.1038/nature.2013.12146.
- ↑ Stanford, John Frederick (1892). The Stanford Dictionary of Anglicised Words and Phrases.
- ↑ «There is some body or other that is of its own nature supremely cold and by participation of which all other bodies obtain that quality». Boyle, Robert (1665). New Experiments and Observations touching Cold.
- ↑ Lambert, Johann Heinrich (1779). Pyrometrie. Berlin. OCLC 165756016.
- ↑ «Cold». Encyclopædia Britannica (Undécima edición). The LoveToKnow Wiki. 1911. Archivado desde el original el 12 de diciembre de 2007. Consultado el 11 de febrero de 2008.
- ↑ J. Dalton (1802), «Ensayo II. Sobre la fuerza del vapor de agua y de otros líquidos diversos, tanto en el vacío como en el aire» y «Ensayo IV. Sobre la expansión de los fluidos elásticos por el calor», Memorias de la Sociedad Literaria y Filosófica de Manchester, vol. 8, pt. 2, pp. 550-74, 595-602.
- ↑ Gay-Lussac, J. L. (1802), «Recherches sur la dilatation des gaz et des vapeurs», Annales de Chimie XLIII: 137.. Traducción al español (extracto).
- ↑ «ABSOLUTO CERO - DOCUMENTAL DE PBS NOVA (completo)». YouTube. Archivado desde el original el 6 de abril de 2017. Consultado el 23 de noviembre de 2016.
- ↑ Cryogenics. Scienceclarified.com. Recuperado el 22 de julio de 2012.
- ↑ «El Premio Nobel de Física 1913: Heike Kamerlingh Onnes». Nobel Media AB. Consultado el 24 de abril de 2012.
Bibliografía
[editar]- Schachtman, Tom (1999). Absolute Zero and the Conquest of Cold. New York: Houghton Mifflin. pp. 272 págs. ISBN 0395938880.


