Diferencia entre revisiones de «Congruencia (geometría)»
m Revertidos los cambios de 189.188.12.152 (disc.) a la última edición de SeroBOT Etiqueta: Reversión |
Etiqueta: Revertido |
||
| Línea 6: | Línea 6: | ||
Las partes coincidentes de las figuras congruentes<ref>{{Cita web|url=https://www.geogebra.org/m/MXWFRH8J|título=Criterios de Congruencia: LLL, ALA, LAL.}}</ref> se llaman homólogas o correspondientes.[[Archivo:Geom shodnost translace.svg|thumb|Figuras congruentes relacionadas mediante traslación.]] |
Las partes coincidentes de las figuras congruentes<ref>{{Cita web|url=https://www.geogebra.org/m/MXWFRH8J|título=Criterios de Congruencia: LLL, ALA, LAL.}}</ref> se llaman homólogas o correspondientes.[[Archivo:Geom shodnost translace.svg|thumb|Figuras congruentes relacionadas mediante traslación.]] |
||
[[Archivo: Hatch marks.svg|thumb|Figuras congruentes relacionadas mediante reflexión y rotación.]] |
[[Archivo: Hatch marks.svg|thumb|Figuras congruentes relacionadas mediante reflexión y rotación.]] |
||
En [[matemáticas]], dos figuras geométricas son '''congruentes''' si tienen las mismas dimensiones y la misma forma sin importar su posición u orientación,<ref>{{cita libro|título=CK-12|autor=CK-12|editorial=CK-12 Foundation|url=https://books.google.es/books?id=RE-klVrTSsIC&pg=PA192#v=onepage&q&f=false|página= 192|fechaacceso= 17 de diciembre de 2019}}</ref> es decir, si existe una [[isometría]] que los relaciona: una transformación que puede ser de [[traslación]], [[Movimiento de rotación#Transformaciones de rotación|rotación]] o [[reflexión (geometría)|reflexión]]. Las partes relacionadas entre las figuras congruentes se llaman '''homólogas''' o correspondientes. |
En [[matemáticas]], dos figuras geométricas son '''congruentes''' si tienen las mismas dimensiones y la misma forma sin importar su posición u orientación,<ref>{{cita libro|título=CK-12|autor=CK-12|editorial=CK-12 Foundation|url=https://books.google.es/books?id=RE-klVrTSsIC&pg=PA192#v=onepage&q&f=false|página= 192|fechaacceso= 17 de diciembre de 2019}}</ref> es decir, si existe una [[isometría]] que los relaciona: una transformación que puede ser de [[traslación]], [[Movimiento de rotación#Transformaciones de rotación|rotación]] o [[reflexión (geometría)|reflexión]]. Las partes relacionadas entre las figuras congruentes se llaman '''homólogas''' o correspondientes. ,. |
||
== Definición de congruencia en geometría analítica == |
== Definición de congruencia en geometría analítica == |
||
Revisión del 01:38 9 dic 2022
Concepto
Dos o más figuras son congruentes si se cumple que son equivalentes tanto en forma como en tamaño, es decir si sus lados y sus ángulos respectivos tienen la correspondiencia en la medida, aunque su posición y orientación sean distintas.
El símbolo de congruencia es ( ≅ ).
Las partes coincidentes de las figuras congruentes[1] se llaman homólogas o correspondientes.


En matemáticas, dos figuras geométricas son congruentes si tienen las mismas dimensiones y la misma forma sin importar su posición u orientación,[2] es decir, si existe una isometría que los relaciona: una transformación que puede ser de traslación, rotación o reflexión. Las partes relacionadas entre las figuras congruentes se llaman homólogas o correspondientes. ,.
Definición de congruencia en geometría analítica
En la geometría euclidiana, la congruencia es equivalente a igualdad matemática en aritmética y álgebra. En geometría analítica, la congruencia puede ser definida así: dos figuras determinadas por puntos sobre un sistema y por de coordenadas cartesianas son congruentes si y solo si, la distancia euclidiana entre cualquier par de puntos de la primera figura es igual a la distancia euclidiana entre los puntos correspondientes de la segunda figura
Definición formal: Dos subconjuntos A y B de un espacio euclídeo son llamados congruentes si existe una isometría con .
Ángulos congruentes
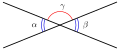
Los ángulos opuestos son congruentes debido a que una rotación de 180° sobre su vértice hace coincidir uno y el otro.
-
Los ángulos y son congruentes y opuestos por el vértice.
-
Una recta que corta dos paralelas generan ángulos congruentes.
-
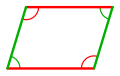
Los ángulos opuestos de un paralelogramo son congruentes.
Congruencia de triángulos
Dos triángulos son congruentes cuando sus lados correspondientes tienen la misma longitud y sus ángulos correspondientes tienen la misma medida.
Notación: Si dos triángulos y son congruentes, esto se notará como:
Criterios de congruencia de triángulos
Criterios para establecer que dos triángulos sean congruentes con un mínimo de condiciones, a veces llamado de forma genérica postulados o teoremas de congruencia ya que aunque triviales se tienen que demostrar.[3][4][5] En principio se busca construir triángulos congruentes con el mínimo de información sobre este.
1. Caso AAL o ALA: Dos triángulos son congruentes si tienen iguales dos de sus ángulos respectivos y el lado entre ellos. En un triángulo si conocemos dos de sus ángulos el tercer ángulo queda unívocamente determinado.
-
ALA
-
AAL
2. Caso LAL: Dos triángulos son congruentes si tienen dos lados iguales y el mismo ángulo comprendido entre ellos.
-
LAL
3. Caso LLL: Dos triángulos son congruentes si tienen los tres lados iguales.
4. Caso LLA: Dos triángulos son congruentes si tienen dos lados y el ángulo sobre uno de ellos iguales. Este caso no es de congruencia si no damos más información sobre el triángulo, como la de ser triángulo rectángulo o si tiene o no ángulos obtusos.
Véase también
Relaciones aritméticas entre ángulos:
Relaciones posicionales entre ángulos:
- Ángulos adyacentes
- Ángulos consecutivos
- Ángulos opuestos por el vértice
- Ángulos interiores y exteriores
Determinados por dos paralelas y una transversal
Referencias
- ↑ «Criterios de Congruencia: LLL, ALA, LAL.».
- ↑ CK-12. CK-12. CK-12 Foundation. p. 192. Consultado el 17 de diciembre de 2019.
- ↑ Clemens y otros. Geometría con aplicaciones y solución de problemas. ISBN 0-201-64407-X
- ↑ Dolciani y otros: Geometría Moderna-
- ↑ CK-12 Geometría, página 222
Enlaces externos
 Wikimedia Commons alberga una categoría multimedia sobre Congruencia.
Wikimedia Commons alberga una categoría multimedia sobre Congruencia.- https://web.archive.org/web/20110905041903/http://www.uv.es/ivorra/Libros/Geometria.pdf
- The SSA en Cut-the-Knot.
- Esta obra contiene una traducción derivada de «Congruence (geometry)» de Wikipedia en inglés, concretamente de esta versión, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.