Diferencia entre revisiones de «Teorema del seno»
Sin resumen de edición Etiquetas: Edición desde móvil Edición vía web móvil |
m Revertidos los cambios de 200.68.140.11 (disc.) a la última edición de Jkbw Etiqueta: Reversión |
||
| Línea 1: | Línea 1: | ||
[[Archivo:Ley de los senos.svg|thumb|Teorema del seno.]]En [[trigonometría]] plana, el '''teorema de los senos'''<ref>Pogorélov. ''Geometría elemental''. Editorial Mir, Moscú(1977)</ref> o también conocido como '''ley de los senos'''<ref>Larson. ''Trigonometría''. ISBN 978-607-481-7-34 (2011)</ref> es una proporción entre las longitudes de los lados de un [[triángulo]] y los [[ |
[[Archivo:Ley de los senos.svg|thumb|Teorema del seno.]]En [[trigonometría]] plana, el '''teorema de los senos'''<ref>Pogorélov. ''Geometría elemental''. Editorial Mir, Moscú(1977)</ref> o también conocido como '''ley de los senos'''<ref>Larson. ''Trigonometría''. ISBN 978-607-481-7-34 (2011)</ref> es una proporción entre las longitudes de los lados de un [[triángulo]] y los [[seno (matemáticas)|senos]] de sus correspondientes [[ángulo]]s opuestos. |
||
Usualmente se presenta de la siguiente forma: |
Usualmente se presenta de la siguiente forma: |
||
Revisión del 14:06 2 oct 2019
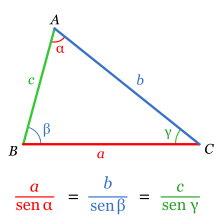
En trigonometría plana, el teorema de los senos[1] o también conocido como ley de los senos[2] es una proporción entre las longitudes de los lados de un triángulo y los senos de sus correspondientes ángulos opuestos.
Usualmente se presenta de la siguiente forma:
|
Historia
Según Ubiratàn D'Ambrosio y Helaine Selin, la ley esférica de los senos fue descubierta en el siglo X. Ha sido indistintamente atribuido a Abu-Mahmud Khojandi, Abu al-Wafa' Buzjani, Nasir al-Din al-Tusi y Abu Nasr Mansur.[3]
El libro de Ibn Muʿādh al-Jayyānī del siglo XI, El libro de los arcos desconocidos de una esfera introdujo la ley general de los senos.[4] La ley plana de los senos fue descrita más tarde en el siglo XIII por Nasīr al-Dīn al-Tūsī. En su Sobre la figura del sector, declaró la ley de los senos para triángulos planos y esféricos, y proporcionó las pruebas de esta ley.[5]
Según Glen Van Brummelen, «La ley de los senos está en realidad basada en Regiomontanus, en sus soluciones de triángulos rectángulos en el Libro IV, y estas soluciones fueron a su vez las bases de sus soluciones de los triángulos generales.»[6] Regiomontanus fue un matemático alemán del siglo XV.
Demostración
A pesar de ser de los teoremas trigonométricos más usados y de tener una demostración particularmente simple, es poco común que se presente o discuta la misma en cursos de trigonometría, de modo que es poco conocida.

Dado el triángulo ABC, denotamos por O su circuncentro y dibujamos su circunferencia circunscrita. Prolongando el segmento BO hasta cortar la circunferencia, se obtiene un diámetro BP.
Ahora, el triángulo PCB es recto, puesto que BP es un diámetro, y además los ángulos A y P son congruentes, porque ambos son ángulos inscritos que abren el segmento BC (Véase definición de arco capaz). Por definición de la función trigonométrica seno, se tiene
donde R es el radio de la circunferencia. Despejando 2R obtenemos:
Repitiendo el procedimiento con un diámetro que pase por A y otro que pase por C, se llega a que las tres fracciones tienen el mismo valor 2R y por tanto son iguales.
La conclusión que se obtiene suele llamarse teorema de los senos generalizado y establece:
|
Puede enunciarse el teorema de una forma alternativa:
|
Aplicación
El teorema de los senos es utilizado para resolver problemas en los que se conocen dos ángulos del triángulo y un lado opuesto a uno de ellos. También se usa cuando conocemos dos lados del triángulo y un ángulo opuesto a uno de ellos.
Puede ser empleado la ley de los senos, con reajustes circunstanciales, en:
- Cálculo de la altura de un árbol
- Hallar el ángulo de elevación del suelo
- Plano para construcción de puentes
- Estudio y dibujo de carriles de una autopista
- Itinerario de un planeo
- Ubicación de un foco de incendio
- Situación de un transmisor de radio clandestino
- La altitud de una montaña y otros casos.[7]
Relación con el área del triángulo

Para un triángulo ABC, el área se calcula como ah/2 donde h es la medida de la altura sobre la base a. Nuevamente, por definición de seno, se tiene sen C = h/b o lo que es lo mismo h = b sen C, de modo que se cumple:
- .
Sin embargo, el teorema de los senos implica que c = 2R sen C, por lo que al substituir en la expresión anterior se obtiene un nuevo teorema:
|
Referencias
- ↑ Pogorélov. Geometría elemental. Editorial Mir, Moscú(1977)
- ↑ Larson. Trigonometría. ISBN 978-607-481-7-34 (2011)
- ↑ Sesiano just lists al-Wafa as a contributor. Sesiano, Jacques (2000) "Islamic mathematics" pp. 137–157, in Selin, Helaine; D'Ambrosio, Ubiratan (2000), Mathematics Across Cultures: The History of Non-western Mathematics, Springer, ISBN 1-4020-0260-2.
- ↑ O'Connor, John J.; Robertson, Edmund F., «Abu Abd Allah Muhammad ibn Muadh Al-Jayyani» (en inglés), MacTutor History of Mathematics archive, Universidad de Saint Andrews, https://mathshistory.st-andrews.ac.uk/Biographies/Al-Jayyani/.
- ↑ Berggren, J. Lennart (2007). «Mathematics in Medieval Islam». The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook. Princeton University Press. p. 518. ISBN 978-0-691-11485-9.
- ↑ "The Law of Sines is really Regiomontanus's foundation for his solutions of right-angled triangles in Book IV, and these solutions are in turn the bases for his solutions of general triangles." Glen Van Brummelen (2009). "The mathematics of the heavens and the earth: the early history of trigonometry". Princeton University Press. p.259. ISBN 0-691-12973-8
- ↑ Larson. Op. cit






