Diferencia entre revisiones de «Distribución binomial»

Distribución binomial
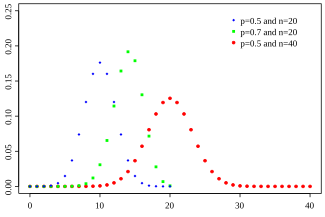	; Función de probabilidad
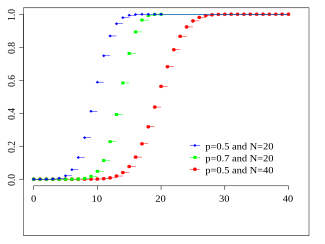	; Función de distribución de probabilidad
Parámetros	número de ensayos (entero); probabilidad de éxito (real)
Dominio
Función de probabilidad (fp)
Función de distribución (cdf)
Media
Mediana	Uno de
Moda
Varianza
Coeficiente de simetría
Curtosis
Entropía
Función generadora de momentos (mgf)
Función característica
	[editar datos en Wikidata]

Explorar historial interactivamente

← Ir a diferencia anterior Ir a siguiente diferencia →

Contenido eliminado Contenido añadido

VisualWikitexto

En renglón

Revisión del 03:28 16 oct 2020

En estadística, la distribución binomial es una distribución de probabilidad discreta que cuenta el número de éxitos en una secuencia de n ensayos de Bernoulli independientes entre sí, con una probabilidad fija p de ocurrencia del éxito entre los ensayos. Un experimento de Bernoulli se caracteriza por ser dicotómico, esto es, solo dos resultados son posibles. A uno de estos se denomina «éxito» y tiene una probabilidad de ocurrencia p y al otro, «fracaso», con una probabilidad^[2] q = 1 - p. En la distribución binomial el anterior experimento se repite n veces, de forma independiente, y se trata de calcular la probabilidad de un determinado número de éxitos. Para n = 1, la binomial se convierte, de hecho, en una distribución de Bernoulli.

Para representar que una variable aleatoria X sigue una distribución binomial de parámetros n y p, se escribe:

X\sim B(n,p)\,

La distribución binomial es la base del test binomial de significación estadística.

Ejemplos

Las siguientes situaciones son ejemplos de experimentos que pueden modelizarse por esta distribución:

Se lanza un dado 5 veces y se cuenta el número Y de tres obtenidos: entonces X ~ B(5, 1/6).
Se responde (al azar) un examen de 10 preguntas, cada una con 4 opciones de respuestas y solo una de ellas correcta. La variable aleatoria discreta X = número de preguntas correctamente contestadas tiene una distribución X ~ B(10, 1/4).

Experimento binomial

Existen muchas situaciones en las que se presenta una experiencia binomial. Cada uno de los experimentos es independiente de los restantes (la probabilidad del resultado de un experimento no depende del resultado del resto). El resultado de cada experimento ha de admitir sólo dos categorías (a las que se denomina éxito y fracaso). El valor de ambas posibilidades ha de ser constante en todos los experimentos, y se denotan como p y q respectivamente, o p y 1-p de forma alternativa.

Se designa por X a la variable que mide el número de éxitos que se han producido en los n experimentos.

Cuando se dan estas circunstancias, se dice que la variable X sigue una distribución de probabilidad binomial, y se denota B(n,p).

Características analíticas

Su función de probabilidad es

\!f(x)={n \choose x}p^{x}(1-p)^{n-x},\,\,\,\,0\leq p\leq 1

donde $x=\{0,1,2,\dots ,n\},$

siendo $\!{n \choose x}={\frac {n!}{x!(n-x)!}}\,\!$ las combinaciones de $n\,\!$ sobre $x\,\!$ ( $n\,\!$ elementos tomados de $x\,\!$ en $x\,\!$ ).

Donde:

$n$ : número de ensayos.
$p$ : probabilidad de éxito.
$X$ : variable aleatoria binomial.^[3]

Ejemplo

Supongamos que se lanza un dado (con 6 caras) 51 veces y queremos conocer la probabilidad de que el número 3 salga 20 veces.

En este problema un ensayo consiste en lanzar el dado una vez. Consideramos un éxito si obtenemos un 3; caso contrario, si no sale 3 consideramos un fracaso. Definimos X = el número de veces que se obtiene un 3 en 51 lanzamientos.

En este caso tenemos una X ~ B(51, 1/6) y la probabilidad sería P(X=20):

\!P(X=20)={51 \choose 20}(1/6)^{20}(1-1/6)^{51-20}=0.0000744\,\!

Propiedades

\mathbb {E} [X]=np\,

Demostración: Por definición, $\mathbb {E} [X]=\sum _{x=0}^{n}x{\binom {n}{x}}p^{x}(1-p)^{n-x}\,$ , para $x=0$ el primer término de la suma desaparece y obtenemos $\mathbb {E} [X]=\sum _{x=1}^{n}x{\binom {n}{x}}p^{x}(1-p)^{n-x}\,$ , luego recordemos que ${\binom {n}{x}}={\frac {n!}{x!(n-x)!}}={\frac {n}{x}}{\frac {(n-1)!}{(x-1)!((n-1)-(x-1))!}}={\frac {n}{x}}{\binom {n-1}{x-1}}$ , para $x\geq 1$ .

Sustituyendo lo anterior en la expresión de $\mathbb {E} [X]$ , tenemos que $\mathbb {E} [X]=\sum _{x=1}^{n}x{\frac {n}{x}}{\binom {n-1}{x-1}}p^{x}(1-p)^{n-x}=n\sum _{x=1}^{n}{\binom {n-1}{x-1}}p^{x}(1-p)^{n-x}\,$ . Note que en este paso, las $x$ se han cancelado y el factor " $n$ " sale de la suma por ser constante, finalmente por la fórmula de Newton (Teorema del binomio) tenemos que $(a+b)^{n}=\sum _{i=0}^{n}{\binom {n}{i}}a^{i}b^{n-i}$ , entonces en la formula anterior basta con elegir $i=x-1,a=p,b=1-p$ tenemos:

$\mathbb {E} [X]=n\sum _{i=0}^{n-1}{\binom {n-1}{i}}p^{i+1}(1-p)^{(n-1)-i}$

sacando una $p$ de la suma tenemos:

$\mathbb {E} [X]=np\sum _{i=0}^{n-1}{\binom {n-1}{i}}p^{i}(1-p)^{(n-1)-i}$ .

$\mathbb {E} [X]=np(p+1-p)^{n-1}=np(1)=np$ .

Otra forma más sencilla es la siguiente, sabemos que si $X,Y$ son variables aleatorias entonces $\mathbb {E} [X+Y]=\mathbb {E} [X]+\mathbb {E} [Y]$ tenemos que una variable aleatoria binomial es la suma de $n$ variables tipo Bernoulli, entonces $\mathbb {E} [X]=\mathbb {E} [X_{1}+X_{2}+\cdots +X_{n}]=\mathbb {E} [X_{1}]+\mathbb {E} [X_{2}]+\cdots +\mathbb {E} [X_{n}]=p+p+\cdots +p=np$ .

\mathbb {V} {\text{ar}}[X]=np(1-p)\,

Relaciones con otras variables aleatorias

Si $n$ tiende a infinito y $p$ es tal que el producto entre ambos parámetros tiende a $\lambda \,\!$ , entonces la distribución de la variable aleatoria binomial tiende a una distribución de Poisson de parámetro $\lambda$ .

Por último, se cumple que cuando $p$ =0.5 y n es muy grande (usualmente se exige que $n\geq 30$ ) la distribución binomial puede aproximarse mediante la distribución normal.

Propiedades reproductivas

Dadas m variables binomiales independientes de parámetros n_i (i = 1,..., m) y $p$ , su suma es también una variable binomial, de parámetros n₁+... + n_m, y $p$ , es decir,

Y=\sum _{i=1}^{m}X_{i}\sim B(\sum _{i=1}^{m}n_{i},p)\,

Véase también

Referencias

↑ Hamza, K. (1995). The smallest uniform upper bound on the distance between the mean and the median of the binomial and Poisson distributions. Statist. Probab. Lett. 23 21–25.
↑ Mode, Elmer B. (1990). Elementos de probabilidad y estadística. Reverte. p. 171. ISBN 9788429150926. Consultado el 5 de diciembre de 2017.
↑ «Distribución binomial». https://matemovil.com (en español.).

Enlaces externos

Wikimedia Commons alberga una categoría multimedia sobre Distribución binomial.
Tablas de la distribución binomial, hasta n=20, en formato PDF.
Calculadora Distribución binomial
Cálculo de la probabilidad de una distribución binomial con R (lenguaje de programación)
Generación estadística de la distribución binomial con números aleatorios usando Python (lenguaje de programación)

Datos: Q185547
Multimedia: Binomial distributions / Q185547

[1] Hamza, K. (1995). The smallest uniform upper bound on the distance between the mean and the median of the binomial and Poisson distributions. Statist. Probab. Lett. 23 21–25.

[2] Mode, Elmer B. (1990). Elementos de probabilidad y estadística. Reverte. p. 171. ISBN 9788429150926. Consultado el 5 de diciembre de 2017.

[3] «Distribución binomial». https://matemovil.com (en español.).

[1]

[2]

[3]

@@ Línea 74: / Línea 74: @@
 Por definición, <math>\mathbb{E}[X] = \sum_{x=0}^{n}x\binom{n}{x}p^x(1-p)^{n-x}\,</math>, para <math>x=0</math> el primer término de la suma desaparece y obtenemos <math>\mathbb{E}[X] = \sum_{x=1}^{n}x\binom{n}{x}p^x(1-p)^{n-x}\,</math>, luego recordemos que <math>\binom{n}{x}=\frac{n!}{x!(n-x)!}=\frac{n}{x}\frac{(n-1)!}{(x-1)!((n-1)-(x-1))!}=\frac{n}{x}\binom{n-1}{x-1}</math>, para <math> x \geq 1</math>.
-Sustituyendo lo anterior en la expresión de <math>\mathbb{E}[X]</math>, tenemos que <math>\mathbb{E}[X] = \sum_{x=1}^{n}x\frac{n}{x}\binom{n-1}{x-1}p^x(1-p)^{n-x}=n\sum_{x=1}^{n}\binom{n-1}{x-1}p^x(1-p)^{n-x}\,</math>. Note que en este paso, las <math>x</math> se han cancelado y el factor "<math>n</math>" sale de la suma por ser constante, finalmente por la fórmula de Newton (Teorema del binomio) tenemos que <math>(a+b)^n=\sum_{i=0}^{n}\binom{n}{i}a^ib^{n-i}</math>, entonces en la formula anterior basta con elegir <math>i=x-1, a=p, b=1-p</math> tenemos que:
+Sustituyendo lo anterior en la expresión de <math>\mathbb{E}[X]</math>, tenemos que <math>\mathbb{E}[X] = \sum_{x=1}^{n}x\frac{n}{x}\binom{n-1}{x-1}p^x(1-p)^{n-x}=n\sum_{x=1}^{n}\binom{n-1}{x-1}p^x(1-p)^{n-x}\,</math>. Note que en este paso, las <math>x</math> se han cancelado y el factor "<math>n</math>" sale de la suma por ser constante, finalmente por la fórmula de Newton (Teorema del binomio) tenemos que <math>(a+b)^n=\sum_{i=0}^{n}\binom{n}{i}a^ib^{n-i}</math>, entonces en la formula anterior basta con elegir <math>i=x-1, a=p, b=1-p</math> tenemos:
 <math>\mathbb{E}[X] =n\sum_{i=0}^{n-1}\binom{n-1}{i}p^{i+1}(1-p)^{(n-1)-i}</math>