Diferencia entre revisiones de «Cero»
Sin resumen de edición Etiquetas: Reversión manual Revertido |
m Revertidos los cambios de 46.100.8.136 (disc.) a la última edición de Pllager Etiquetas: Reversión Revertido |
||
| Línea 34: | Línea 34: | ||
El número cero se puede representar como cualquier número más su opuesto (o, equivalentemente, menos él mismo): {{math|X + }}({{math|–X}}){{math| {{=}}}} 0. |
El número cero se puede representar como cualquier número más su opuesto (o, equivalentemente, menos él mismo): {{math|X + }}({{math|–X}}){{math| {{=}}}} 0. |
||
Algunos consideran que el cero es un número "tanto positivo como negativo".<ref>https://proofwiki.org/wiki/Zero_is_both_Positive_and_Negative</ref> |
* Algunos consideran que el cero es un número "tanto positivo como negativo".<ref>https://proofwiki.org/wiki/Zero_is_both_Positive_and_Negative</ref> |
||
== Etimología == |
== Etimología == |
||
Revisión del 13:45 2 ene 2024
| 0 | ||||
|---|---|---|---|---|
| Cardinal | Cero | |||
| Sistemas de numeración | ||||
| Arábiga oriental | ٠ | |||
| Ática | O | |||
| Jónica | Ο | |||
| China | 零/〇 | |||
| Egipcia |
| |||
| Maya |
| |||
| India | 0 | |||
| Sistema binario | 0 | |||
| Sistema octal | 0 | |||
| Sistema hexadecimal | 0 | |||
| Lista de números | ||||

El cero (0) es un numeral de la propiedad par. Es el signo numérico de valor nulo, que en notación posicional ocupa los lugares donde no hay una cifra significativa. Si está situado a la derecha de un número entero se multiplica por 10 su valor;[1] colocado a la izquierda, no lo modifica.
Utilizándolo como número, se pueden realizar con él operaciones algebraicas como sumas, restas, multiplicaciones, entre otras. Pero, por ser la expresión del valor nulo (nada, nadie, ninguno...), puede dar lugar a expresiones indeterminadas o que carecen de sentido.
Es el elemento del conjunto ordenado de los números enteros (ℤ, ≤) que sigue al –1 y precede al 1.
Algunos matemáticos lo consideran perteneciente al conjunto de los naturales (ℕ) ya que estos también se pueden definir como el conjunto que nos permite contar el número de elementos que contienen los demás conjuntos, y el conjunto vacío tiene ningún elemento, en algunos estudios el cero no se considera un natural. Cuando la inclusión o no del cero en los números naturales es relevante se especifica en la notación, indicando ℕ0 como el conjunto de los naturales incluyendo el cero y ℕ+ como el conjunto de los naturales excluyendo el cero.
El número cero se puede representar como cualquier número más su opuesto (o, equivalentemente, menos él mismo): X + (–X) = 0.
- Algunos consideran que el cero es un número "tanto positivo como negativo".[2]
Etimología
La palabra «cero» llega al castellano desde el italiano zero, y esta del bajo latín zephyrum;[3] esta palabra proviene de la traducción del nombre sánscrito shunya (vacío) al árabe ṣifr (صفر). El matemático italiano Fibonacci (c. 1170-1250), que creció en el norte de África y a quien se atribuye la introducción del sistema decimal en Europa, ya utilizó el término zephyrum con este sentido. Este se convertiría en zefiro en italiano, y luego se contrajo a zero en veneciano. Cabe señalar que la palabra italiana zefiro ya existía previamente, pero con el significado de "viento del oeste", y provenía (como ya mencionamos) del bajo latín, que a su vez lo tomó del griego zephyrus; esta última palabra pudo haber influido en la ortografía utilizada al transcribir el vocablo árabe ṣifr al italiano.[4] En cuanto a la voz española «cifra», ya es derivación directa de ṣifr.
Uso moderno
Dependiendo del contexto, puede haber diferentes palabras utilizadas para el número cero, o el concepto de cero. Para la simple noción de carencia, se utilizan a menudo las palabras "nada" y "ninguno". A veces, se utiliza la palabra "nought" o "naught".
A menudo se dice "oh" en el contexto de la lectura de una cadena de dígitos, como número de teléfono, direcciones, números de tarjeta de crédito, hora militar o años (por ejemplo, el código de área 201 se pronunciaría "dos oh uno"; un año como 1907 se pronuncia a menudo "diecinueve oh siete"). La presencia de otros dígitos, que indican que la cadena sólo contiene números, evita la confusión con la letra O. Por este motivo, los sistemas que incluyen cadenas con letras y números (por ejemplo, código postal canadiense) pueden excluir el uso de la letra O.
Las palabras de argot para cero incluyen "zip", "zilch", "nada" y "scratch".[5]
"Nil" se utiliza para muchos deportes en inglés británico. Varios deportes tienen palabras específicas para una puntuación de cero, como "love" en tenis – del francés l'œuf, "el huevo" – y "duck" en cricket, una abreviación de "duck's egg"; "goose egg" es otro término de argot general utilizado para cero.[5]
Historia
Antiguas y grandes civilizaciones —como las del Antiguo Egipto, Babilonia, la Antigua Grecia y la Civilización maya— poseen documentos de carácter matemático o astronómico mostrando símbolos indicativos del valor cero; pero por diversas peculiaridades de sus sistemas numéricos, no supieron obtener el verdadero beneficio de este capital descubrimiento.[6]
En el sistema de numeración egipcio se utilizó el signo «-nfr-»
para indicar el cero (en el Papiro Boulaq 18, datado hacia el 1700 a. C.).
El cero apareció por primera vez en Babilonia en el siglo III a. C., aunque su escritura en tablillas de arcilla se remonta al 2000 a. C. Los babilonios escribían en arcilla sin cocer, sobre superficies planas o tablillas. Su notación era cuneiforme. En tablillas datadas en el año 1700 a. C. se ven anotaciones numéricas en su particular forma. Los babilonios utilizaban un sistema de base 60. Con su sistema de notación no era posible distinguir el número 23 del 203 o el 2003, aunque esta ambigüedad no pareció preocuparles.
Alrededor del 400 a. C., los babilonios comenzaron a colocar el signo de «dos cuñas» en los lugares donde en nuestro sistema escribiríamos un cero, que se leía «varios». Las dos cuñas no fueron la única forma de mostrar las posiciones del cero; en una tablilla datada en el 700 a. C. encontrada en Kish, antigua ciudad de Mesopotamia al este de Babilonia, utilizaron un signo de «tres ganchos». En otras tablillas usaron un solo «gancho» y, en algunos casos, la deformación de este se asemeja a la forma del cero.


El cero también surgió en Mesoamérica e ideado por las civilizaciones mesoamericanas antes de la era cristiana, por la cultura maya. Posiblemente fue utilizado antes por la cultura olmeca.
El primer uso documentado mostrando el número cero corresponde al año 36 a. C., haciendo uso de la numeración maya. A causa de la anomalía introducida en el tercer lugar de su notación posicional, les privó de posibilidades operativas.[7]
Claudio Ptolomeo en el Almagesto, escrito en 130 d. C., usaba el valor de «vacío» o «0». Ptolomeo solía utilizar el símbolo entre dígitos o al final del número. Podría pensarse que el cero habría arraigado entonces, pero lo cierto es que Ptolomeo no usaba el símbolo como «número» sino que lo consideraba un signo de anotación. Este uso no se difundió, pues muy pocos lo adoptaron.
Los romanos no utilizaron el cero. Sus números eran letras de su alfabeto; para representar cifras usaban: I, V, X, L, C, D, M, agrupándolas. Para números con valores iguales o superiores a 4000, dibujaban una línea horizontal sobre el «número», para indicar que el valor se multiplicaba por 1000.
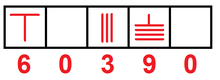
El Sūnzĭ Suànjīng, de fecha desconocida pero que se estima que data del siglo I al V d. C., y los registros japoneses que datan del siglo XVIII, describen cómo el sistema de barras de conteo chino del siglo IV a. C. permitía realizar cálculos decimales. Como se señala en Suanjing de Xiahou Yang (425–468 d. C.) que establece que para multiplicar o dividir un número por 10, 100, 1000 o 10000, todo lo que se necesita hacer, con las varillas en el tablero de conteo, es moverlas hacia adelante, o hacia atrás, por 1, 2, 3 o 4 lugares.[8] Según A History of Mathematics, las barras "daron la representación decimal de un número, con un espacio vacío que indica cero". El sistema de barra de conteo se considera un sistema de notación posicional.
El cero posicional
La civilización india es la cuna de la notación posicional, de uso casi universal en el siglo XXI. Es posible que el matemático indio Brahmagupta (siglo VI) fuera el primero en teorizar sobre el concepto de «cero» no solo como definición de una cantidad nula, sino como posible sumando para números negativos y positivos. El primer testimonio del uso del «cero indio» está datado en el año 683: una inscripción camboyana de Angkor Wat, tallada en piedra, que incluye el número «605».[9] Otras pruebas de uso se datan hacia el año 810. Las inscripciones de Gwalior están datados en 875-876.[10] Abu Ja'far Mujammad ibn Musa (Al-Juarismi), en su obra titulada «Tratado de la adición y la sustracción mediante el cálculo de los indios» explica el principio de numeración posicional decimal, señalando el origen indio de las cifras. La décima figura, que tiene forma redondeada, es el «cero».[11]
Los árabes lo transmitieron por el Magreb y Al-Ándalus, pasando posteriormente al resto de Europa. Los primeros manuscritos que muestran las cifras indias (llamadas entonces «árabes») provienen del norte de España y son del siglo X: el Codex Vigilanus y el Codex Aemilianensis. El cero no figura en los textos, pues los cálculos se realizaban con ábaco, y su uso aparentemente no era necesario.
Aunque se atribuyen los primeros usos del cero en Francia, o al controvertido papa Silvestre II, alrededor del año 1000, la mayor parte de las referencias indican que el cero (llamado zefhirum) fue introducido en Europa por el matemático italiano Fibonacci en el siglo XII, mostrando el álgebra árabe en su Liber abaci (El libro del ábaco), aunque por la facilidad del nuevo sistema, las autoridades eclesiásticas lo tildaron de mágico o demoniaco.[12]
Representaciones del cero
El cero se representa en textos occidentales con la cifra «0». Desde el siglo XX, y especialmente con el desarrollo de la informática, es frecuente que este signo aparezca cortado por una barra diagonal (/), nueva notación que evitaba la confusión con la grafía de la letra «o». Hasta hace poco, la conjunción disyuntiva «o» debía llevar tilde: «ó», cuando iba escrita entre cifras para no ser confundida con el signo numérico 0. Actualmente, dicha regla no está en vigor.[13]
Representación gráfica del valor cero
En coordenadas cartesianas el origen de coordenadas se asocia al valor 0 (cero).
El cero y los números naturales
El cero, por ser un concepto numérico especial, no se incluía en el conjunto de los números naturales ℕ, por convenio. Se representaba como ℕ0, al conjunto de los números naturales cuando incluye al cero, por ello es posible encontrar muchos libros donde los autores no consideran al cero como número natural. De hecho, aún no hay consenso al respecto.
A algunos matemáticos les resulta conveniente tratarlo como a los otros números naturales, por eso la discrepancia. Desde un punto de vista histórico el cero aparece tan tarde que algunos no creen que sea justo llamarlo natural.
Operaciones matemáticas con el cero
Cero en la suma
En la suma, el cero es el elemento neutro; es decir, cualquier número a sumado con 0 vuelve a dar a. Ejemplo: 25 + 0 = 25. O sea, todo número sumado con 0 es el mismo número.
Cero en la resta
En la resta, el cero es el elemento neutro; es decir, cualquier número a restado con 0 vuelve a dar a, excepto cuando el cero es el minuendo, en cuyo caso resulta -a. Ejemplos:
- 37 – 0 = 37
- 0 - 37 = -37
Cero en la multiplicación
En el producto, el cero es el elemento absorbente; cualquier número operado con 0 da 0. Ejemplo: 25 × 0 = 0
Cero en la división
El cero puede ser dividido por otros números, en cuyo caso es el elemento absorbente (ejemplo: 0:25 = 0). El cero no puede dividir a ningún número.
División por cero en los números reales
En los números reales (incluso en los complejos) la división entre cero es una indeterminación; así, las expresiones:
- 8⁄0; 0⁄0
carecen de sentido.
Intuitivamente, significa que no tiene 'sentido' «repartir» 8 manzanas entre niños de un aula vacía. Tampoco tiene 'sentido', distribuir 0 billetes entre cero personas: nada entre nadie.
Matemáticamente, el cero es el único número real por el cual no se puede dividir. Por eso 0 es el único real que no tiene inverso multiplicativo.
Ejemplo:
- x⁄2 = x · 1⁄2 (correcto).
- x⁄0 = x · 1⁄0 (incorrecto porque 1⁄0 no es un número real).
Cero en la división de límites
En el análisis matemático existen definiciones de distintos tipos de límites. Por ejemplo:
- ,
- ,
- .
Sin embargo, si se analiza cada numerador y denominador por separado, el límite de todo ellos es cero. Por eso se dice que 0⁄0 es indeterminado, pues pueden obtenerse resultados tan diferentes como infinito, uno o cero.
Cero en la potenciación
- Si a es distinto de 0, entonces
- Si n es mayor de 0, entonces
El valor no está definido como potencia, pero según el contexto o por comodidad se puede elegir uno de los resultados mediante una definición. Algunas calculadoras científicas dan 1 como resultado.
En el contexto de los límites, es una indeterminación pues los límites de potencias tales que los límites de base y exponente por separado son cero, pueden terminar dando cualquier cosa.
Paridad
En el conjunto de los enteros, ℤ el 0 es un número par; satisface la definición de paridad, así como también todas las características de los números pares.

El cero en la Identidad de Euler
El cero, junto con los números 1, π, i, e están relacionados en la célebre Identidad de Euler:
- eiπ + 1 = 0
Matemática avanzada
En otra ramas de la matemática, especialmente en el álgebra, se llama «cero» y se simboliza también con «0» a elementos de otros conjuntos muy diferentes de los reales. Es el caso del vector nulo en el conjunto de los vectores del plano o del espacio. En general se le dice cero al elemento neutro de un grupo abeliano.
Sistemas digitales
El 0 se asocia con la posición de «apagado» en lógica positiva (el 1 se asocia con la posición de «encendido») y es uno de los dos dígitos (0 y 1) del sistema binario.
Física
El valor cero desempeña un papel especial para muchas magnitudes físicas. Para algunas magnitudes, el nivel cero se distingue de forma natural de todos los demás niveles, mientras que para otras se elige de forma más o menos arbitraria. Por ejemplo, para una temperatura absoluta (medida en kelvins), cero es el valor más bajo posible (temperatura negativas están definidas, pero los sistemas de temperatura negativa no son realmente más fríos). Esto contrasta, por ejemplo, con las temperaturas de la escala Celsius, en la que el cero se define arbitrariamente como el punto de congelación del agua. Al medir la intensidad del sonido en decibelioss o fonios, el nivel cero se fija arbitrariamente en un valor de referencia, por ejemplo, en el valor del umbral de audición. En física, la energía del punto cero es la energía más baja posible que puede poseer un sistema físico de mecánica cuántica. puede poseer un sistema físico y es la energía del estado terreno del sistema.
Cero absoluto
El cero absoluto es, en el campo de la física, la temperatura más baja que teóricamente puede alcanzar la materia. Esta temperatura da lugar a la escala Kelvin, que establece como 0 K dicha temperatura. Su equivalencia en grados Celsius es de –273,15 °C.
Véase también
Referencias
- ↑ En notación posicional decimal.
- ↑ https://proofwiki.org/wiki/Zero_is_both_Positive_and_Negative
- ↑ Real Academia Española. «cero». Diccionario de la lengua española (23.ª edición). Consultado el 3 de octubre de 2022.
- ↑ Ifrah, Georges. The Universal History of Numbers: From Prehistory to the Invention of the Computer (en inglés). Wiley. ISBN 978-0-471-39340-5.
- ↑ a b 'Aught' synonyms Archivado el 23 de agosto de 2014 en Wayback Machine., Thesaurus.com - Retrieved April 2013.
- ↑ Ifrah:1998 p. 785.
- ↑ Ifrah:1998 p. 786.
- ↑ Hollings, Christopher D (10 de noviembre de 2016). «‘Mathematical Biography: A MacTutor Celebration’». BSHM Bulletin: Journal of the British Society for the History of Mathematics 32 (3): 265-265. ISSN 1749-8430. doi:10.1080/17498430.2016.1244749. Consultado el 4 de julio de 2023.
- ↑ El increíble descubrimiento en Angkor Wat del primer cero escrito por el hombre - El arqueólogo matemático Amir Aczel halló el número 605 escrito en una estela del siglo VI, desaparecida durante la dictadura de los Jemeres rojos, ABC, 22/11/2014.
- ↑ Ifrah:1998 p. 909.
- ↑ Ifrah:1998 p. 828.
- ↑ Ifrah:1998 pp. 1357-1358.
- ↑ «Entrada en la sección online de consultas de la RAE». Consultado el 12 de agosto de 2015. « Por lo tanto, a partir de este momento, la conjunción o se escribirá siempre sin tilde, como corresponde a su condición de palabra monosílaba átona, con independencia de que aparezca entre palabras, cifras o signos [..]».
Bibliografía
- Ifrah, Georges (1998): Historia universal de las cifras. Espasa Calpe S.A. ISBN 84-239-9730-8
- Charles Seife (2006): Cero, La biografía de una idea peligrosa. EllagoEdiciones-Colección Las Islas.
- Villamil, J., & Riscanevo, L. (2020). Perspectivas históricas y epistemológicas del número cero. Praxis & Saber, 11(26), e9847. https://doi.org/10.19053/22160159.v11.n26.2020.9847
- Dantzig, Tobias (1954): El número, lenguaje de la ciencia. Hobbs-Sudamericana S.A. Buenos Aires
Enlaces externos
- Historia del Cero
- Weisstein, Eric W. «Zero». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- https://revistas.uptc.edu.co/index.php/praxis_saber/article/view/9847/9288











