Diferencia entre revisiones de «Poliedro flexible»
Rescatando 1 referencia(s) y marcando 0 enlace(s) como roto(s)) #IABot (v2.0.9.5 |
m Borrando parámetros que no existen en eswiki y dan error |
||
| Línea 58: | Línea 58: | ||
* {{citation|first=R.|last=Bricard|title=Mémoire sur la théorie de l'octaèdre articulé|journal=J. Math. Pures Appl.|volume=5|issue=3|year=1897|pages=113–148|url=http://portail.mathdoc.fr/JMPA/afficher_notice.php?id=JMPA_1897_5_3_A5_0|access-date=2008-07-27|archive-url=https://web.archive.org/web/20120216011406/http://portail.mathdoc.fr/JMPA/afficher_notice.php?id=JMPA_1897_5_3_A5_0|archive-date=2012-02-16}} |
* {{citation|first=R.|last=Bricard|title=Mémoire sur la théorie de l'octaèdre articulé|journal=J. Math. Pures Appl.|volume=5|issue=3|year=1897|pages=113–148|url=http://portail.mathdoc.fr/JMPA/afficher_notice.php?id=JMPA_1897_5_3_A5_0|access-date=2008-07-27|archive-url=https://web.archive.org/web/20120216011406/http://portail.mathdoc.fr/JMPA/afficher_notice.php?id=JMPA_1897_5_3_A5_0|archive-date=2012-02-16}} |
||
* {{Citation | last1=Connelly | first1=Robert | title=A counterexample to the rigidity conjecture for polyhedra | url=http://www.numdam.org/item?id=PMIHES_1977__47__333_0 | mr=0488071 | year=1977 | journal=[[ Publications Mathématiques de l'IHÉS]] | issn=1618-1913 | issue=47 | pages=333–338 | doi=10.1007/BF02684342 | volume=47}} |
* {{Citation | last1=Connelly | first1=Robert | title=A counterexample to the rigidity conjecture for polyhedra | url=http://www.numdam.org/item?id=PMIHES_1977__47__333_0 | mr=0488071 | year=1977 | journal=[[ Publications Mathématiques de l'IHÉS]] | issn=1618-1913 | issue=47 | pages=333–338 | doi=10.1007/BF02684342 | volume=47}} |
||
* {{Citation | last1=Connelly | first1=Robert | last2=Sabitov | first2=I. | last3=Walz | first3=Anke | title=The bellows conjecture | mr=1447981 | year=1997 | journal=Beiträge zur Algebra und Geometrie | issn=0138-4821 | volume=38 | issue=1 | pages=1–10 | url=http://emis.ams.org/journals/BAG/vol.38/no.1/1.html | fechaacceso=2 de febrero de 2021 | fechaarchivo=9 de julio de 2008 | urlarchivo=https://web.archive.org/web/20080709005955/http://www.emis.ams.org/journals/BAG/vol.38/no.1/1.html |
* {{Citation | last1=Connelly | first1=Robert | last2=Sabitov | first2=I. | last3=Walz | first3=Anke | title=The bellows conjecture | mr=1447981 | year=1997 | journal=Beiträge zur Algebra und Geometrie | issn=0138-4821 | volume=38 | issue=1 | pages=1–10 | url=http://emis.ams.org/journals/BAG/vol.38/no.1/1.html | fechaacceso=2 de febrero de 2021 | fechaarchivo=9 de julio de 2008 | urlarchivo=https://web.archive.org/web/20080709005955/http://www.emis.ams.org/journals/BAG/vol.38/no.1/1.html }} |
||
* {{citation |
* {{citation |
||
| last = Gaifullin | first = Alexander A. |
| last = Gaifullin | first = Alexander A. |
||
Revisión del 06:44 18 jul 2024

En geometría, un poliedro flexible es un poliedro (más precisamente, una superficie poliédrica que carece de algunas caras en su contorno exterior), cuya forma se puede cambiar continuamente sin alterar la forma de ninguna de sus caras. El teorema de rigidez de Cauchy demuestra que en la dimensión 3 dicho poliedro no puede ser convexo (esto también es cierto en dimensiones superiores).
Los primeros ejemplos de poliedros flexibles, ahora llamados octaedros de Bricard, fueron descubiertos por Bricard (1897). Son superficies auto-intersecadas isométricas con respecto a un octaedro. El primer ejemplo de una superficie flexible que no se interseca a sí misma en , la esfera de Connelly, fue descubierta por Connelly (1977). El poliedro de Steffen es otro ejemplo de poliedro flexible que no se auto-interseca derivado del octaedro de Bricard.[1]
Conjetura de los fuelles
A finales de la década de 1970, Connelly y Dennis Sullivan formularon la conjetura de los fuelles, afirmando que el volumen de un poliedro flexible es invariante bajo flexión. Esta conjetura fue probada para poliedros homeomorfos a una esfera por Sabitov (1995) usando teoría de eliminación, y luego fue probado para superficies poliédricas bidimensionales orientables generales por Connelly (1997). La prueba extiende la fórmula de Piero della Francesca para el volumen de un tetraedro a una fórmula para el volumen de cualquier poliedro. La fórmula extendida muestra que el volumen debe ser una raíz de un polinomio cuyos coeficientes dependen solo de las longitudes de las aristas del poliedro. Dado que las longitudes de los bordes no pueden cambiar a medida que se flexiona el poliedro, el volumen debe permanecer en una de las finitas raíces del polinomio, en lugar de cambiar continuamente.[2]
Seccionamiento congruente
Connelly conjeturó que el invariante de Dehn de un poliedro flexible se mantiene invariante bajo flexión. Esto se conoció como la conjetura de los fuelles fuerte o (después de que se probó en 2018) el teorema de los fuelles fuerte.[3]
La curvatura media total de un poliedro flexible, definida como la suma de los productos de las longitudes de las aristas por sus ángulos diedros exteriores, es una función del invariante de Dehn que también se sabe que permanece constante mientras un poliedro se flexiona.[4]
Generalizaciones
Los polícoros flexibles en el espacio euclidiano de 4 dimensiones y el espacio hiperbólico de 3 dimensiones fueron estudiados por Stachel (2000).Gaifullin (2014) construyó politopos flexibles en dimensiones.
Ejemplos
-
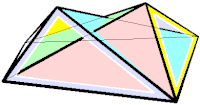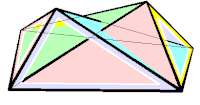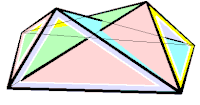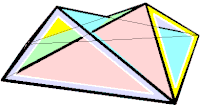
Octaedro de Bricard flexible del primer tipo
-
Octaedro de Bricard flexible del segundo tipo
-
Poliedro de Steffen flexible
-
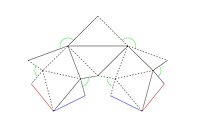
Desplegable del politopo de Steffen
Véase también
Referencias
Bibliografía
Fuentes primarias
- Alexander, Ralph (1985), «Lipschitzian mappings and total mean curvature of polyhedral surfaces. I», Transactions of the American Mathematical Society 288 (2): 661-678, JSTOR 1999957, MR 776397, doi:10.2307/1999957..
- Alexandrov, Victor (2010), «The Dehn invariants of the Bricard octahedra», Journal of Geometry 99 (1–2): 1-13, MR 2823098, arXiv:0901.2989, doi:10.1007/s00022-011-0061-7..
- Bricard, R. (1897), «Mémoire sur la théorie de l'octaèdre articulé», J. Math. Pures Appl. 5 (3): 113-148, archivado desde el original el 16 de febrero de 2012, consultado el 27 de julio de 2008.
- Connelly, Robert (1977), «A counterexample to the rigidity conjecture for polyhedra», Publications Mathématiques de l'IHÉS 47 (47): 333-338, ISSN 1618-1913, MR 0488071, doi:10.1007/BF02684342.
- Connelly, Robert; Sabitov, I.; Walz, Anke (1997), «The bellows conjecture», Beiträge zur Algebra und Geometrie 38 (1): 1-10, ISSN 0138-4821, MR 1447981, archivado desde el original el 9 de julio de 2008, consultado el 2 de febrero de 2021.
- Gaifullin, Alexander A. (2014), «Flexible cross-polytopes in spaces of constant curvature», Proceedings of the Steklov Institute of Mathematics 286 (1): 77-113, MR 3482593, arXiv:1312.7608, doi:10.1134/S0081543814060066..
- Gaĭfullin, A. A.; Ignashchenko, L. S. (2018), «Dehn invariant and scissors congruence of flexible polyhedra», Trudy Matematicheskogo Instituta Imeni V 302 (Topologiya i Fizika): 143-160, ISBN 5-7846-0147-4, MR 3894642, doi:10.1134/S0371968518030068..
- Sabitov, I. Kh. (1995), «On the problem of the invariance of the volume of a deformable polyhedron», Rossiĭskaya Akademiya Nauk. Moskovskoe Matematicheskoe Obshchestvo. Uspekhi Matematicheskikh Nauk 50 (2): 223-224, ISSN 0042-1316, MR 1339277.
- Stachel, Hellmuth (2006), «Flexible octahedra in the hyperbolic space», en A. Prékopa, ed., Non-Euclidean geometries (János Bolyai memorial volume), Mathematics and its Applications 581, New York: Springer, pp. 209-225, ISBN 978-0-387-29554-1, MR 2191249, doi:10.1007/0-387-29555-0_11 Parámetro desconocido
|citeseerx=ignorado (ayuda).. - Stachel, Hellmuth (2000), «Flexible cross-polytopes in the Euclidean 4-space», Journal for Geometry and Graphics 4 (2): 159-167, MR 1829540..
Fuentes secundarias
- Connelly, Robert (1979), «The rigidity of polyhedral surfaces», Mathematics Magazine 52 (5): 275-283, JSTOR 2689778, MR 551682, doi:10.2307/2689778..
- Connelly, Robert (1981), «Flexing surfaces», en Klarner, David A., ed., The Mathematical Gardner, Springer, pp. 79-89, ISBN 978-1-4684-6688-1, doi:10.1007/978-1-4684-6686-7_10..
- Connelly, Robert (1993), «Rigidity», Handbook of convex geometry, Vol. A, B, Amsterdam: North-Holland, pp. 223-271, MR 1242981..
- Demaine, Erik D.; O'Rourke, Joseph (2007), «23.2 Flexible polyhedra», Geometric Folding Algorithms: Linkages, origami, polyhedra, Cambridge University Press, Cambridge, pp. 345-348, ISBN 978-0-521-85757-4, MR 2354878, doi:10.1017/CBO9780511735172 Parámetro desconocido
|title-link=ignorado (ayuda).. - Fuchs, Dmitry; Tabachnikov, Serge (2007), «Lecture 25. Flexible polyhedra», Mathematical Omnibus: Thirty lectures on classic mathematics, Providence, RI: American Mathematical Society, pp. 345-360, ISBN 978-0-8218-4316-1, MR 2350979, doi:10.1090/mbk/046.
Enlaces externos
- Weisstein, Eric W. «Poliedro flexible». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Weisstein, Eric W. «Conjetura de los fuelles». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.