Discusión:Límite de una función

EN TRADUCCIÓN

Definición formal

Límite de una función en un punto

...

Sometimes, the limit is also defined considering for x values different from p. (which would be a relative limit - that is, a limit considering a restriction to the domain - using the already given definition). For such definition we have:

$\lim _{x\to p}f(x)=L\Leftrightarrow \forall _{\varepsilon >0}\exists _{\delta >0}\forall _{x\in \mathbb {D} }\ 0<|x-p|<\delta \Rightarrow |f(x)-L|<\varepsilon$

It is just a particular case of functions on metric spaces, with both M and N are the real numbers.

Or we write

$\lim _{x\to p}f(x)=\infty$

if and only if

for every R > 0 there exists a δ > 0 such that for all real numbers x with 0 < |x-p| < δ, we have f(x) > R;

or we write

$\lim _{x\to p}f(x)=-\infty$

if and only if

for every R < 0 there exists a δ > 0 such that for all real numbers x with 0 < |x-p| < δ, we have f(x) < R.

This definition can be condensed by using the concept of Neighbourhood, which also allows expressions such as $\lim _{x\to +\infty }f(x)=L$. We write

$\lim _{x\to p}f(x)=L$ (where $x\in {\overline {\mathbb {D} }}$

and $p;L\in {\tilde {\mathbb {R} }}$) if and only if

$\forall _{\varepsilon >0}\exists _{\delta >0}\forall _{x\in \mathbb {D} }\ x\in B_{\delta }(p)\Rightarrow f(x)\in B_{\varepsilon }(L)$

If, in the definitions, x-p is used instead of |x-p|, then we get a right-handed limit, denoted by lim_x→p+. If p-x is used, we get a left-handed limit, denoted by lim_x→p-. See main article one-sided limit.

Limit of function at infinity

Limit of a function at infinity exists if, for every ε > 0 there exists a S > 0 ; so that |f(x)-L| < ε for all x > S.

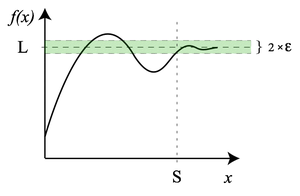
Suppose f(x) is a real-valued function. We can also consider the limit of function when x increases or decreases indefinitely.

We write

$\lim _{x\to \infty }f(x)=L$

if and only if

for every ε > 0 there exists S >0 such that for all real numbers x>S, we have |f(x)-L|<ε

or we write

$\lim _{x\to \infty }f(x)=\infty$

for every R > 0 there exists S >0 such that for all real numbers x>S, we have f(x)>R.

Similarly, we can define the expressions

$\lim _{x\to \infty }f(x)=-\infty ,\lim _{x\to -\infty }f(x)=L,\lim _{x\to -\infty }f(x)=\infty ,\lim _{x\to -\infty }f(x)=-\infty$.

There are three basic rules for evaluating limits at infinity for a rational function f(x) = p(x)/q(x):

• If the degree of p is greater than the degree of q, then the limit is positive or negative infinity depending on the signs of the leading coefficients
• If the degree of p and q are equal, the limit is the leading coefficient of p divided by the leading coefficient of q
• If the degree of p is less than the degree of q, the limit is 0

If the limit at infinity exists, it represents a horizontal asymptote at x = L. Polynomials do not have horizontal asymptotes; they may occur with rational functions.

Complex-valued functions

The complex plane with metric $d(x,y):=|x-y|$ is also a metric space. There are two different types of limits when we consider complex-valued functions.

Limit of a function at a point

Suppose f is a complex-valued function, then we write

$\lim _{x\to p}f(x)=L$

if and only if

for every ε > 0 there exists a δ >0 such that for all real numbers x with 0<|x-p|<δ, we have |f(x)-L|<ε

It is just a particular case of functions over metric spaces with both M and N are the complex plane.

Limit of a function at infinity

We write

$\lim _{x\to \infty }f(x)=L$

if and only if

for every ε > 0 there exists S >0 such that for all complex numbers |x|>S, we have |f(x)-L|<ε

test

Limit of a function of more than one variable

By noting that |x-p| represents a distance, the definition of a limit can be extended to functions of more than one variable.

$\lim _{(x,y)\to (p,q)}f(x,y)=L$

if and only if

for every ε > 0 there exists a δ > 0 such that for all real numbers x with 0 < ||(x,y)-(p,q)|| < δ, we have |f(x,y)-L| < ε

where ||(x,y)-(p,q)|| represents the Euclidean distance. This can be extended to any number of variables.