Sudoku

Sudoku (en japonés: 数独, sūdoku) es un rompecabezas matemático de colocación que se popularizó en Japón en 1986 y se dio a conocer en el ámbito internacional en 2005. El objetivo es rellenar una cuadrícula de 9×9 celdas dividida en subcuadrículas (también llamadas "cajas" o "regiones") de 3×3 de las cifras del 1 al 9 partiendo de algunos números ya dispuestos en algunas de las celdas. No se debe repetir ninguna cifra en una misma fila, columna o subcuadrícula. Un sudoku está bien planteado si la solución es única. La resolución del problema requiere paciencia y ciertas dotes lógicas.

Ejemplo de sudoku.

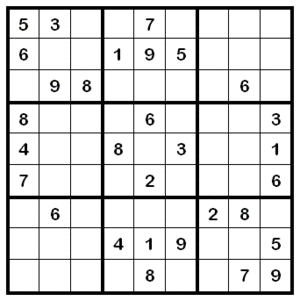
En realidad, no es estrictamente necesario utilizar números, sino que se pueden utilizar letras, formas o colores sin alterar las reglas, pero se utilizan números por conveniencia. La cuadrícula más común es de 9×9 con regiones de 3×3, pero también se utilizan otros tamaños. Además, las regiones no tienen por qué ser cuadradas, aunque generalmente lo son.

La solución de un sudoku siempre es un cuadrado latino, aunque el recíproco en general no es cierto ya que el sudoku establece la restricción añadida de que no se puede repetir un mismo número en una región.

Numerosos periódicos han empezado a publicar el sudoku en 2005 en su sección de pasatiempos. En España, El País publica en su sección dominical infantil Pequeño País una cuadrícula de 4×4 dividida en regiones de 2×2 que llama minisudoku. A partir del lunes 11 de julio de 2005 El País publica un sudoku diariamente de lunes a sábado, en el que se indica el nivel de dificultad, que oscila entre "muy fácil " y "difícil". El Mundo ha empezado a publicar el sudoku habitual de 9×9 el 20 de junio de 2005. En Colombia, el semanario El Espectador inició su publicación el 3 de julio de 2005.

Historia

El rompecabezas puede haberse originado en Nueva York a finales de los años 1970 bajo el nombre de Number Place (El lugar de los números) en la revista Math Puzzles and Logic Problems (Rompecabezas matemáticos y problemas lógicos) de la empresa especializada en rompecabezas Dell. No se sabe el nombre del que diseñó y creó el primer puzzle de este tipo, aunque probablemente fue Walter Mackey, uno de los diseñadores de puzzles de Dell.

Posteriormente, Nikoli lo exportó a Japón, publicándolo en el periódico Monthly Nikolist en abril de 1984 bajo el título "Sūji wa dokushin ni kagiru" (数字は独身に限る), que se puede traducir como "los números deben estar solos" (独身 significa literalmente "célibe, soltero"). Fue Kaji Maki (鍜治 真起), presidente de Nikoli, quien le puso el nombre. Posteriormente, el nombre se abrevió a Sūdoku (数独; sū = número, doku = solo); ya que es práctica común en japonés tomar el primer kanji de palabras compuestas para abreviarlas.

En 1986, Nikoli introdujo dos innovaciones que garantizarían la popularidad del rompecabezas: el número de cifras que venían dadas estaría restringida a un máximo de 30 y los puzzles serían "simétricos" (es decir, las celdas con cifras dadas estarían dispuestas de forma rotacionalmente simétricas).

Métodos de resolución

La región 3x3 de la esquina superior izquierda debe contener un 7. Rastreando a lo largo y ancho los sietes localizados en cualquier lugar de la rejilla, el jugador puede eliminar todas las celdas vacías de la esquina superior izquierda que no pueden contener un 7. Esto deja sólo una celda posible (remarcada en verde).

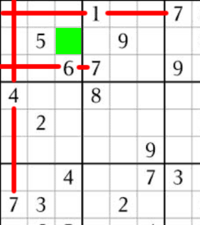
La estrategia para resolver un puzle se puede considerar como la combinación de tres procesos: escaneo, marcado y análisis.

Escaneo

El escaneo se realiza desde el principio y periódicamente, durante toda la resolución. El escaneo puede tener que ser ejecutado varias veces entre periodos de análisis. El escaneo consta de dos técnicas básicas: trama cruzada y recuento, que pueden usarse alternativamente.

• Trama cruzada, se trata del escaneo de filas (o columnas) para identificar qué línea en una región particular puede contener un número determinado mediante un proceso de eliminación. Este proceso se repite entonces con las columnas (o filas). Para obtener resultados más rápidos, los números son escaneados de forma ordenada, según su frecuencia de aparición. Es importante realizar este proceso sistemáticamente, comprobando todos los dígitos del 1 al 9.
• Recuento 1-9 por regiones, filas y columnas para identificar números perdidos. El recuento basado en el último número descubierto puede aumentar la velocidad de la búsqueda. También puede ser el caso (es típico en puzles más difíciles) que el valor de una celda individual pueda ser determinado mediante un recuento inverso, esto es, escaneando su región, fila o columna para valores que no pueden ser, para ver cuál es el que falta.

Los resolutores avanzados buscan "contingencias" mientras escanean, esto es, acotan la ubicación de un número con una fila, columna o región o dos o tres celdas. Cuando esas celdas descansan todas en la misma fila (o columna) y región, pueden usarse con un propósito de eliminación durante la trama cruzada y el recuento (Ejemplo de contingencia en Puzzle Japan). Puzles particularmente desafiantes pueden requerir el reconocimiento de múltiples contingencias, quizás en múltiples direcciones o incluso intersecciones - relegando la mayoría de los resolutores al marcado (como se describe más abajo). Los puzles que pueden ser resueltos sólo mediante escaneo, sin requerir la detección de contingencias se clasifican como puzles "fáciles"; otros puzles más difíciles, por definición, no pueden resolverse únicamente mediante escaneo.

Marcado

El escaneo viene a interrumpirse cuando no pueden descubrirse nuevos números. En este punto es necesario centrarse en algún análisis lógico. La mayoría encuentra útil guiar este análisis mediante el marcado de números candidatos en las celdas vacías. Hay dos notaciones populares: subíndices y puntos. En la notación de subíndice, los números candidatos se escriben en pequeño en las celdas. La desventaja es que los puzles originales son publicados en periódicos que habitualmente no dejan demasiado espacio para acomodar más de unos pocos dígitos. Si se usa esta notación, los resolutores crean, a menudo, una copia más grande de el puzle y emplean un lapiz afilado. La segunda notación es un patrón de puntos con un punto en la esquina superior izquierda representando un 1 y un punto en la esquina inferior derecha representando un 9. Esta notación tiene como ventaja que puede usarse en el puzle original. Se requiere destreza para el emplazamiento de los puntos, porque puntos desplazados o marcas inadvertidas llevan, inevitablemente, a confusión y no son fáciles de borrar sin añadir más confusión.

Análisis

Hay dos aproximaciones principales - eliminación y "y-si".

• En eliminación, el progreso se realiza mediante la sucesiva eliminación de números candidatos para una o más celdas, hasta dejar sólo una elección. Después de lograr cada respuesta, debe realizarse un nuevo escaneo (habitualmente comprobando el efecto del último número). Hay una serie de tácticas de eliminación. Una de las más comunes es el "borrado del candidato no coincidente". Las celdas con idéntica configuración de números candidatos se dice que coinciden si la cantidad de números candidatos en cada una es igual al número de celdas que los contienen. Por ejemplo, se dice que celdas coinciden con una particular fila, columna o region si dos celdas contienen el mismo par de números candidatos (p,q) y no otros, o si tres celdas contienen el mismo triplete de números candidatos (p,q,r) y no otros. Estas son, esencialmente, contingencias coincidentes. Estos números (p,q,r) que aparecen como candidatos en cualquier lugar en la misma fila, columna o region en celdas no coincidentes, pueden ser borrados.
• En la aproximación "y-si", se selecciona una celda con sólo dos números candidatos y se realiza una conjetura. Las etapas de arriba se repiten a menos que se encuentre una duplicación, en cuyo caso el candidato alternativo es la solución. En términos lógicos este método se conoce como reducción al absurdo. Nishio es una forma limitada de esta aproximación: para cada candidato para una celda, la cuestión que se plantea: ¿entrará un número particular de una configuración en otro emplazamiento? Si la respuesta es sí, entonces ese candidato puede ser eliminado. La aproximación "y-si" requiere un lapiz y una goma. Esta aproximación puede ser desaprobada por puristas lógicos por demasiado ensayo y error pero puede llegar a soluciones clara y rápidamente.

Idealmente, se necesita encontrar una combinación de técnicas que eviten alguno de los inconvenientes de los elementos de arriba. El recuento de regiones, filas y columnas puede resultar aburrido. Escribir números candidatos en celdas vacías puede consumir demasiado tiempo. La aproximación "y-si" puede ser confusa a menos que seas bien organizado. El quiz de la cuestión es encontrar una técnica que minimice el recuento, el marcado y el borrado.

Resolución por ordenador

Para los programadores es relativamente sencillo construir una búsqueda por el método de "fuerza bruta". Ésta asignaría, típicamente, un valor (supongamos que 1, o el más cercano a 1 disponible) a la primera celda disponible (supongamos que la superior izquierda) y entonces continuar asignando el siguiente valor disponible (supongamos que 2) a la siguiente celda disponible. Esto continuaría hasta que se descubriera una duplicación, en cuyo caso, el siguiente valor alternativo se colocaría en el primer campo alterado. Aunqeu lejos de la eficiencia computacional, este método encontrará la solución si se permite el suficiente tiempo de computación. Un programa más eficiente podría dejar una huella de valores potenciales para las celdas, eliminando valores imposibles hasta que sólo un valor quedase para una celda determinada. Entonces se rellenaría esa celda y se usaría esa información para más eliminaciones y así, sucesivamente hasta el final del puzle. Esto emularía más exactamente lo que un resolutor humano haría sin el método de ensayo y error.

Codificar la búsqueda para imposibilidades basadas en contingencias e incluso múltiples contingencias (como sería requerido para los Sudoku más difíciles) es bastante complejo de construir a mano. De cualquier modo, tales complicaciones son innecesarias si todo lo que el programador desea hacer es encontrar una solución eficientemente. Una forma más eficiente de construir soluciones involucra herramientas de programación más avanzadas.

Algunos programas así construidos, que emulan la resolución humana, permiten estimar la dificultad que tendrá un humano para encontrar la solución.

Enlaces externos

• GNUDoku, programa informático para crear y solucionar puzles "Su Doku"