Congruencia (geometría)

En geometría, dos figuras u objetos son congruentes si tienen la misma forma y tamaño, o si una tiene la misma forma y tamaño que la imagen especular de la otra.[1]
Más formalmente, dos conjuntos de puntos se denominan congruentes si, y solo si, uno puede transformarse en el otro mediante una isometría, es decir, una combinación de movimientos rígidos, a saber, una traslación, una rotación y una reflexión. Esto significa que cualquiera de los objetos puede reposicionarse y reflejarse (pero no redimensionarse) de modo que coincida exactamente con el otro objeto. Por lo tanto, dos figuras planas distintas en un trozo de papel son congruentes si se pueden recortar y luego hacer coincidir completamente. Se permite dar la vuelta al papel.

En geometría elemental la palabra congruente se usa a menudo de la siguiente manera.[2] La palabra igual se usa a menudo en lugar de congruente para estos objetos.
- Dos segmento de líneas son congruentes si tienen la misma longitud.
- Dos ángulos son congruentes si tienen la misma medida.
- Dos círculos son congruentes si tienen el mismo diámetro.
En este sentido, dos figuras planas son congruentes implica que sus correspondientes características son congruentes o iguales incluyendo no sólo sus correspondientes lados y ángulos, sino también sus correspondientes diagonales, perímetros y áreas.
El concepto relacionado de semejanza se aplica si los objetos tienen la misma forma pero no necesariamente el mismo tamaño. (La mayoría de las definiciones consideran que la congruencia es una forma de semejanza, aunque una minoría exige que los objetos tengan tamaños diferentes para calificarlos de semejantes).
Concepto
Dos o más figuras son congruentes si se cumple que son equivalentes tanto en forma como en tamaño, es decir si sus lados y sus ángulos respectivos tienen la correspondiencia en la medida, aunque su posición y orientación sean distintas.
El símbolo de congruencia es ( ≅ ).
Las partes coincidentes de las figuras congruentes[3] se llaman homólogas o correspondientes.


En matemáticas, dos figuras geométricas son congruentes si tienen las mismas dimensiones y la misma forma sin importar su posición u orientación,[4] es decir, si existe una isometría que los relaciona: una transformación que puede ser de traslación, rotación o reflexión. Las partes relacionadas entre las figuras congruentes se llaman homólogas o correspondientes.
Determinación de la congruencia de polígonos
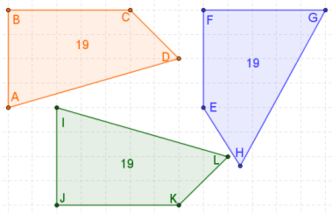
Para que dos polígonos sean congruentes, deben tener el mismo número de lados (y, por tanto, el mismo número de vértices). Dos polígonos con n lados son congruentes si y sólo si cada uno tiene secuencias numéricamente idénticas (incluso en el sentido de las agujas del reloj para un polígono y en el sentido contrario para el otro) lado-ángulo-lado-ángulo-... para n lados y n ángulos.
La congruencia de polígonos puede establecerse gráficamente de la siguiente manera:
- Primero, emparejar y etiquetar los vértices correspondientes de las dos figuras.
- En segundo lugar, dibuja un vector desde uno de los vértices de una de las figuras hasta el vértice correspondiente de la otra figura. Traslada la primera figura mediante este vector para que estos dos vértices coincidan.
- Tercero, gira la figura trasladada alrededor del vértice correspondiente hasta que un par de lados correspondientes coincidan.
- Cuarto, reflejar la figura rotada sobre este lado coincidente hasta que las figuras coincidan.
Si en algún momento no se puede completar el paso, los polígonos no son congruentes.
Definición de congruencia en geometría analítica
En la geometría euclidiana, la congruencia es equivalente a igualdad matemática en aritmética y álgebra. En geometría analítica, la congruencia puede ser definida así: dos figuras determinadas por puntos sobre un sistema y por de coordenadas cartesianas son congruentes si y solo si, la distancia euclidiana entre cualquier par de puntos de la primera figura es igual a la distancia euclidiana entre los puntos correspondientes de la segunda figura
Definición formal: Dos subconjuntos A y B de un espacio euclídeo son llamados congruentes si existe una isometría con .
Ángulos congruentes
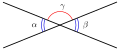
Los ángulos opuestos son congruentes debido a que una rotación de 180° sobre su vértice hace coincidir uno y el otro.
-
Los ángulos y son congruentes y opuestos por el vértice.
-
Una recta que corta dos paralelas generan ángulos congruentes.
-
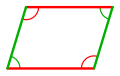
Los ángulos opuestos de un paralelogramo son congruentes.
Congruencia de triángulos
Dos triángulos son congruentes cuando sus lados correspondientes tienen la misma longitud y sus ángulos correspondientes tienen la misma medida.
Simbólicamente, escribimos la congruencia e incongruencia de dos triángulos △ABC y △A′B′C′ como sigue:
En muchos casos basta con establecer la igualdad de las tres partes correspondientes y utilizar uno de los siguientes resultados para deducir la congruencia de los dos triángulos.
Notación: Si dos triángulos y son congruentes, esto se notará como:
Criterios de congruencia de triángulos
Criterios para establecer que dos triángulos sean congruentes con un mínimo de condiciones, a veces llamado de forma genérica postulados o teoremas de congruencia ya que aunque triviales se tienen que demostrar.[5][6][7] En principio se busca construir triángulos congruentes con el mínimo de información sobre este.
1. Caso AAL o ALA: Dos triángulos son congruentes si tienen iguales dos de sus ángulos respectivos y el lado entre ellos. En un triángulo si conocemos dos de sus ángulos el tercer ángulo queda unívocamente determinado.
-
ALA
-
AAL
2. Caso LAL: Dos triángulos son congruentes si tienen dos lados iguales y el mismo ángulo comprendido entre ellos.
-
LAL
3. Caso LLL: Dos triángulos son congruentes si tienen los tres lados iguales.
4. Caso LLA: Dos triángulos son congruentes si tienen dos lados y el ángulo sobre uno de ellos iguales. Este caso no es de congruencia si no damos más información sobre el triángulo, como la de ser triángulo rectángulo o si tiene o no ángulos obtusos.
Lado-lado-ángulo
La condición LLA (lado-lado-ángulo) que especifica dos lados y un ángulo no incluido (también conocida como ASS, o ángulo-lado-lado) no demuestra por sí misma la congruencia. Para demostrar la congruencia se necesita información adicional, como la medida de los ángulos correspondientes y, en algunos casos, las longitudes de los dos pares de lados correspondientes. Hay algunos casos posibles:
Si dos triángulos cumplen la condición SSA y la longitud del lado opuesto al ángulo es mayor o igual que la longitud del lado adyacente (SSA, o lado largo-lado corto-ángulo), entonces los dos triángulos son congruentes. El lado opuesto es a veces más largo cuando los ángulos correspondientes son agudos, pero es siempre más largo cuando los ángulos correspondientes son rectos u obtusos. Cuando el ángulo es recto, también conocido como postulado de la hipotenusa-pierna (HL) o condición del ángulo recto-hipotenusa-lado (RHA), el tercer lado puede calcularse mediante el teorema de Pitágoras, lo que permite aplicar el postulado de la SSS.
Si dos triángulos cumplen la condición SSA y los ángulos correspondientes son agudos y la longitud del lado opuesto al ángulo es igual a la longitud del lado adyacente multiplicada por el seno del ángulo, entonces los dos triángulos son congruentes.
Si dos triángulos cumplen la condición SSA y los ángulos correspondientes son agudos y la longitud del lado opuesto al ángulo es mayor que la longitud del lado adyacente multiplicada por el seno del ángulo (pero menor que la longitud del lado adyacente), entonces no se puede demostrar que los dos triángulos sean congruentes. Este es el caso ambiguo y se pueden formar dos triángulos diferentes a partir de la información dada, pero si se dispone de más información que los distinga se puede demostrar la congruencia.
Ángulo-ángulo-ángulo
En geometría euclídea, AAA (ángulo-ángulo-ángulo) (o simplemente AA, ya que en geometría euclídea los ángulos de un triángulo suman 180°) no proporciona información sobre el tamaño de los dos triángulos y, por tanto, sólo demuestra similitud y no congruencia en el espacio euclídeo.
Sin embargo, en geometría esférica y geometría hiperbólica (donde la suma de los ángulos de un triángulo varía con el tamaño) AAA es suficiente para la congruencia en una curvatura dada de la superficie.[8]
CPCTC
Este acrónimo del inglés Corresponding Parts of Congruent Triangles are Congruent, que significa Partes correspondientes de triángulos congruentes son congruentes, que es una versión abreviada de la definición de triángulos congruentes.[9][10]
En más detalle, es una manera de decir que si los triángulos ABC y DEF son congruentes, es decir,
con los correspondientes pares de ángulos en los vértices A y D; B y E; y C, y con los correspondientes pares de lados AB y DE; BC y EF; y CA y FD, entonces las siguientes afirmaciones son ciertas:
El enunciado se utiliza a menudo como justificación en las pruebas de geometría elemental cuando se necesita una conclusión de la congruencia de las partes de dos triángulos después de haber establecido la congruencia de los triángulos. Por ejemplo, si se ha demostrado que dos triángulos son congruentes por el criterio SSS y en una demostración se necesita una afirmación de que los ángulos correspondientes son congruentes, entonces CPCTC puede usarse como justificación de esta afirmación.
Un teorema relacionado es CPCFC', en el que triángulos se sustituye por figuras de modo que el teorema se aplica a cualquier par de polígonos o poliedros que sean congruentes.
Determinación de la congruencia de polígonos

Para que dos polígonos sean congruentes, deben tener el mismo número de lados (y, por tanto, el mismo número de vértices). Dos polígonos con n lados son congruentes si y sólo si cada uno tiene secuencias numéricamente idénticas (incluso en el sentido de las agujas del reloj para un polígono y en el sentido contrario para el otro) lado-ángulo-lado-ángulo-... para n lados y n ángulos.
La congruencia de polígonos puede establecerse gráficamente de la siguiente manera:
- Primero, emparejar y etiquetar los vértices correspondientes de las dos figuras.
- En segundo lugar, dibuja un vector desde uno de los vértices de una de las figuras hasta el vértice correspondiente de la otra figura. Traslada la primera figura mediante este vector para que estos dos vértices coincidan.
- Tercero, gira la figura trasladada alrededor del vértice correspondiente hasta que un par de lados correspondientes coincidan.
- Cuarto, reflejar la figura rotada sobre este lado coincidente hasta que las figuras coincidan.
Si en algún momento no se puede completar el paso, los polígonos no son congruentes.
Definición de congruencia en geometría analítica
En sistema euclidiano, la congruencia es fundamental; es la contrapartida de la igualdad para los números. En geometría analítica, la congruencia puede definirse intuitivamente así: dos mapeados de figuras sobre un sistema de coordenadas cartesianas son congruentes si y sólo si, para dos puntos cualesquiera del primer mapeado, la distancia euclídea entre ellos es igual a la distancia euclídea entre los puntos correspondientes del segundo mapeado.
Una definición más formal establece que dos subconjuntos A y B del espacio euclídeo Rn se llaman congruentes si existe una isometría f: Rn → Rn (un elemento del grupo euclídeo E(n)) con f(A) = B. La congruencia es una relación de equivalencia.
Véase también
Relaciones aritméticas entre ángulos:
Relaciones posicionales entre ángulos:
- Ángulos adyacentes
- Ángulos consecutivos
- Ángulos opuestos por el vértice
- Ángulos interiores y exteriores
Determinados por dos paralelas y una transversal
Referencias
- ↑ Clapham, C.; Nicholson, J. (2009). «Oxford Concise Dictionary of Mathematics, Congruent Figures». Addison-Wesley. p. 167. Archivado desde el original el 29 de octubre de 2013. Consultado el 2 de junio de 2017.
- ↑ «Congruencia». Math Open Reference. 2009. Consultado el 2 June 2017.
- ↑ «Criterios de Congruencia: LLL, ALA, LAL.».
- ↑ CK-12. CK-12. CK-12 Foundation. p. 192. Consultado el 17 de diciembre de 2019.
- ↑ Clemens y otros. Geometría con aplicaciones y solución de problemas. ISBN 0-201-64407-X
- ↑ Dolciani y otros: Geometría Moderna-
- ↑ CK-12 Geometría, página 222
- ↑ Cornel, Antonio (2002). Geometry for Secondary Schools. Mathematics Textbooks Second Edition. Bookmark Inc. ISBN 971-569-441-1.
- ↑ Jacobs, Harold R. (1974), Geometry, W.H. Freeman, p. 160, ISBN 0-7167-0456-0. Jacobs uses a slight variation of the phrase
- ↑ «Congruent Triangles». Cliff's Notes. Consultado el 4 de febrero de 2014.
Enlaces externos
 Wikimedia Commons alberga una categoría multimedia sobre Congruencia.
Wikimedia Commons alberga una categoría multimedia sobre Congruencia.- https://web.archive.org/web/20110905041903/http://www.uv.es/ivorra/Libros/Geometria.pdf
- The SSA en Cut-the-Knot.
- Esta obra contiene una traducción derivada de «Congruence (geometry)» de Wikipedia en inglés, concretamente de esta versión, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.