Ir al contenido

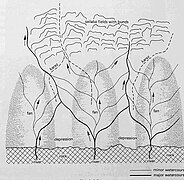
Modelo de escorrentía

De Wikipedia, la enciclopedia libre
Esta es una versión antigua de esta página, editada a las 22:31 18 feb 2020 por InternetArchiveBot (discusión · contribs.). La dirección URL es un enlace permanente a esta versión, que puede ser diferente de la versión actual.
Esquematización del ciclo hidrológico

Un modelo de escorrentía es una representación que forma parte del ciclo hidrológico en cuanto al fenómeno de la escorrentía superficial de una cuenca hidrográfica. El modelo se usa mayormente para entender el proceso de escurrimiento y para pronosticarlo con el propósito de regularizar el uso del agua o diseñar obras hidráulicas para el control de inundaciónes.

Aunque se podrían hacer modelos a escala, la gran mayoría de los modelos de la escorrentía son modelos matemáticos.

Clases de modelos

Análisis de la frecuencia acumulada del caudal un río, modelo estadístico
Factores hidrológicos en el proceso de la escorrentía

Los modelos matemáticos de la escorrentía se pueden clasificar como:[1]​

  • modelos estadísticos
  • modelos empíricos
  • modelos conceptuales
  • modelos de transporte
  • modelos compuestos

Modelos estadísticos

Los modelos estadísticos están basados en el análisis de frecuencia acumulada de las escorrentías. Los pronósticos a base del período de retorno sirven para evaluar la frecuencia de escasez o de exceso de agua con el propósito de regularizar el uso del agua o diseñar obras hidráulicas para el control de inundaciónes.

Además, el análisis estadístico de la lluvia o de la precipitación permite de estimar las recargas hidrológicas respresentativas de la cuenca que después pueden servir como datos de entrada en los modelos matemáticos que convierten las recargas en escorrentías, de modo que se puede evaluar el régimen de la escorrentía.

Modelos empíricos

Hidrograma de tormenta debido a la lluvia recibida en la cuenca

Los modelos empíricos son modelos, o más bien métodos, que se desarrollaron por experiencia, relacionando parámetros físicos hidrológicos con el fin de derivar la escorrentía a base de ellos. Modelos empíricos bien conocidos son:

Mapa esquemático del modelo SHETRAN de la cuenca hidrográfica de Dunsop, Bowland forest, Reino Unido

Modelos conceptuales

Una cuenca hidrológica subdividida en subcuencas

Los modelos conceptuales son modelos basados en algún idea o concepto del proceso de la conversión de la lluvia en escorrentía.[3]​

Un ejemplo del modelo conceptual es el modelo del reservorio como detallado más abajo.[4]​

Modelos de transporte

Los modelos de transporte hidráulico son modelos matemáticos a base de ecuaciones hidráulicas usadas en la mecánica de fluidos, como la de Saint Venant, para el flujo del agua en el lecho o cauce del río.

El transporte del agua se hace normalmente por ciertos tramos del río definidos por una división de la cuenca entera en subcuencas.

La complejidad de las características de la superficie de cuencas hace que los modelos de transporte todavía no son aplicables al proceso de escorrentía hasta el momento que el agua llega a un lecho o cauce bien definido.[5]​ Por ello estos modelos se usan para el caso que el agua ya entró en un arroyo o río.

Software Ejemplos de software: DSSAM,[6]​ DUFLOW,[7]​ HSPF,[8]​ MIKE,[9]​ MOHID Land,[10]​ TopModel,[11]​ WAFLEX[12]​ y el modelo Xinanjiang[13]​

Modelos compuestos

Los modelos compuestos son modelos que tienen componentes de los modelos conceptuales y de transporte.

Software Ejemplos de software: GSSHA,[14]​ HBV,[15]​ SHETRAN[16]​ y Vflo[17]​

La distinción entre modelos compuestos y modelos de transporte no es siempre muy clara porque muchos modelos de transporte también incluyen elementos de modelos conceptuales para determinar la cantidad de agua que entra en el cauce del río, en tanto que el método de la determinación puede variar de bien simple a muy avanzado.

Galería de ilustraciones

Modelo del reservorio

Un modelo bien conocido es el modelo del reservorio lineal, pero en la práctica este modelo tiene utilidad limitada.

El modelo de escorrentía a base del reservorio no lineal tiene más aplicabilidad universal, pero solamente vale para cuencas en las cuales se puede considerar que la lluvia tiene una distribución más o menos igual sobre el área. El tamaño máximo de la cuenca depende entonces de las características de la precipitación en la región. Cuando el área de estudio es demasiado grande, se puede dividirlo en subcuencas y las hidrogramas respectivas pueden ser combinadas empleando modelos de simulación o modelos hidráulicos de transporte.

Reservorio lineal

Figura 1. Principios del reservorio lineal

La hidrología de un reservorio lineal (figura 1) está basada en dos ecuaciones:[18]​

  • (1) ecuación del flujo: * Q = A.S
  • (2) ecuación de continuidad o balance de agua: * R = Q + dS/dT

siendo:

  • Q, la escorrentía, el escurrimiento o la descarga superficial hidráulica en unidades [L/T], en que L indica el espesor de una lámina (mm, m) y T el tiempo (hora, dia)
  • R, la recarga hidráulica neta, la lluvia efectiva o la precipitación excesiva [L/T]
  • A, el factor de reacción constante, o factor de respuesta, con unidad [1/T]
  • S', el almacenamiento o abastecimiento del agua con unidad [L]
  • dS, una diferencial, o infinitesimal, o incremento pequeño de S
  • dT, una diferencial, o infinitesimal, o incremento pequeño de T

Ecuación de la escorrentía
La combinación de las dos ecuaciones anteriores resulta en una ecuación diferencial la solución de la cual se presenta como:

  • Q2 = Q1 exp { – A (T2 – T1) } + R [ 1 – exp { – A (T2 – T1) } ]

Este es la ecuación de la escorrentía, del escurrimiento, o de la descarga superficial hidráulica, donde Q1 y Q2 significan los valores de Q al tiempo T1 y T2 respectivamente mientras que T2–T1 es el paso o intervalo en el tiempo durante el cual la recarga neta R se puede suponer constante.

Computación del hidrograma total

Provisto que el valor de A es conocido se puede obtener el hidrograma total (HT) utilizando un número sucesivo de pasos en el tiempo y calculando la escorrentía con la ecuación de la escorrentía al final de cada paso partiendo de la escorrentía al final del intervalo previo. La escorrentía inicial debe estar conocido también.

Hidrograma unitario Cuando R = 0, la descarga se puede escribir como:

  • Q = – dS/dT

Sustituyendo la expresión de Q en la ecuación (1) se obtiene la ecuación diferencial

  • dS/dT = – A.S

y su solución es:

  • S = exp(– A.T)

Reemplazando S por Q/A de acuerdo a la ecuación (1) y tomando una undidad de tiempo (T=1), se ve que:

  • Q = A exp(– A.T)

Esta se llama hidrograma unitaria instantánea (HUI[19]​). La disponibilidad del HUI elimina la necesidad de calcular el HT sumando los hidrogamas parciales con el método más complicado de la convolución.[20]​

Factor de reacción Cuando el factor de reacción (A) se deja determinar a partir de las características de la cuenca hidrológica, el modelo del reservorio se puede emplear como modelo determinístico o modelo analítico.

De otro modo, el factor A se puede determinar de un archivo de datos de lluvia y escorrentía usando el método de calibración explicado más abajo para el reservorio no lineal. Con este método el reservorio se utiliza como caja negra.

Conversiones

  • 1 mm/día corresponde a 10 m3/día por ha de la cuenca;
  • 1 l/seg por ha corresponde a 8.64 mm/día o 86.4 m3/día por ha.

Reservorio no lineal

Figura 2. Principios del reservorio no lineal
Figura 3. Relación entre el factor de reacción Aq (Alpha) y la escorrentía superficial (Q), valle Rogbom
Figura 4. Hidrograma observada y reconstruida (simulada) con el modelo del reservorio no lineal, valle de Rogbom
Figura 5. Conversión de la lluvia en lluvia efectiva (recarga neta) por medio del ante-reservorio, valle de Rogbom

Contrario al reservorio lineal, el reservorio no lineal tiene un factor de reacción (A) que no es constante,[21]​ sino una función que depende de S o Q (figura 2, 3).

Normalmente el factor A aumenta con Q o S porque cuando más elevado el nivel del agua más grande la capacidad de descarga. Por ello, el factor se llama Aq en vez de A. El reservorio no lineal no tiene un HUI utilizable.

Durante períodos sin lluvia y recarga, o sea R = 0, la ecuación de escorrentía se reduce a:

  • Q2 = Q1 exp { – Aq (T2 – T1) }

o empleando un intervalo unitario del tiempo T2 – T1 = 1 y solucionando para Aq:

  • Aq = – ln (Q2/Q1)

Entonces, el factor de reacción Aq se puede derivar de la escorrentía o descarga con intervalos unitarios durante épocas secas mediante un método numérico[22]​

La figura 3 muestra la relación entre Aq y Q para un valle pequeño (Rogbom) en Sierra Leone.
La figura 4 muestra el hidrograma observado y el simulado (calculado, reconstruido) del arroyo al lado aguas abajo del mismo valle.[23]​

Recarga neta

La recarga neta (lluvia efectiva, precipitación excesiva) se puede modelar con un ante-reservorio (figura 6) que da la recarga como desborde. El prereservorio contiene los siguientes elementos:

  • un almacenamiento máximo (Sm) con unidad [L]
  • un almacenamiento actual (Sa) con unidad [L]
  • un almacenamiento relativo: Sr = Sa/Sm
  • una velocidad de escape máxima (Em) en unidades [L/T] correspondiendo con la velocidad máxima de la evapotranspiración mas la infiltración o sea la percolación (recarga al agua subterránea en el acuífero) que no participan en el proceso del escurrimiento
  • una velocidad de escape actual: Ea = Sr.Em
  • un déficit de almacenamiento Sd = Sm + Ea – Sa
Figura 6. Esquema del reservorio no lineal con un ante-reservorio para determinar la recarga efectiva

La recarga durante un intervalo unitario de tiempo (T2–T1=1) se encuentra como: R = Lluvia – Sd, a condición que R > 0, si no R = 0.

El almacenamiento actual al final del intervalo unitario se calcula como Sa2 = Sa1 + Lluvia – R – Ea, donde Sa1 es al almacenamiento actual al comienzo del intervalo de tiempo.

El método del Número de Curva (NC)[2]​ presenta una alternativa para estimar la recarga neta. Aquí, la abstracción inicial es comparable con Sm–Si donde Si es el valor inicial de Sa en el método del reservorio.

Software Las figuras 3, 4 y 5 han sido preparadas con el programa de computadora RainOff[24]​ diseñado para analizar la relación lluvia-escorrentía por medio de un reservorio no lineal con un pre-reservorio. El programa determina la función de Aq como lineal, logarítmico, o exponencial. El programa también contiene un ejemplo del hidrograma de un sistema de drenaje subterráneo agrario con un valor del factor de reacción Aq que se deja calcular directamente de las características del sistema mismo.[18]​

Referencias

  1. ↑ J.Boonstra (1994) Estimating peak runoff rates, Chapter 4 in: H.P.Ritzema (Ed.), Drainage Principles and Applications, Publication 16, International Institute for Land Reclamation and Improvement, Wageningen, The Netherlands, ISBN 90 70754 3 39
  2. ↑ a b método del número de curva
  3. ↑ Rushton, K.R. (2003) Groundwater Hydrology: Conceptual and Computational Models. John Wiley and Sons Ltd. ISBN 0-470-85004-3
  4. ↑ RainOff [1] a rainfall-runoff model based on the concept of a nonlinear reservoir.
  5. ↑ Vijay P. Singh (1995) Computer Models of Watershed Hydrology, Water Resource Publications, pgs. 563-594
  6. ↑ DSSAM model
  7. ↑ «DuFlow model». Archivado desde el original el 10 de diciembre de 2017. Consultado el 9 de diciembre de 2017. 
  8. ↑ Hydrological Simulation Program Fortan (HSPF)
  9. ↑ MIKE model
  10. ↑ MOHID Land model]
  11. ↑ TopModel
  12. ↑ WAFLEX model
  13. ↑ «Xinanjiang model». Archivado desde el original el 15 de mayo de 2011. Consultado el 12 de junio de 2010. 
  14. ↑ GSSHA model
  15. ↑ HBV model
  16. ↑ Shetran model
  17. ↑ Vflo model
  18. ↑ a b J.W. de Zeeuw (1973) Hydrograph analysis for areas with mainly groundwater runoff. In: Principles and Applications, Vol. II, Chapter 16, Theories of field drainage and watershed runoff. p 321-358. Publication 16, International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands.
  19. ↑ Instantneous Unit Hydrograph
  20. ↑ D.A. Kraijenhoff van de Leur (1973) Rainfall-runoff relations and computational models. In: Drainage Principle and Applications, Vol. II, Chapter 16, Theories of field drainage and watershed runoff. p 245-320. Publication 16, International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands.
  21. ↑ ILRI (1995). Land drainage and soil salinity: some Mexican experiences. In: ILRI Annual Report 1995, p. 44-53. International Institute for Land Reclamation and Improvement, Wageningen (ILRI), Wageningen, The Netherlands. On line: [2]
  22. ↑ Teoría del reservorio no lineal [3]
  23. ↑ A.Huizing (1988) Rainfall-Runoff relations in a small cultivated valley in Sierra Leone. Wetland Utilization Research Project. International Institute for Land Reclamation and Improvement, Wageningen, The Netherlands
  24. ↑ RainOff, a computer model for rainfall-runoff relations using the concept of a non-linear reservoir. Bajar de : [4]
Obtenido de «https://es.wikipedia.org/eswiki/w/index.php?title=Modelo_de_escorrentía&oldid=123656357»