Espiral logarítmica

Una espiral logarítmica, espiral equiangular o espiral de crecimiento es una clase de curva espiral que aparece frecuentemente en la naturaleza. Su nombre proviene de la expresión de una de sus ecuaciones: $\theta =\log _{b}(r/a)\,$

Historia

El término espiral logarítmica se debe a Pierre Varignon. La espiral logarítmica fue estudiada por Descartes y Torricelli, pero la persona que le dedicó un libro fue Jakob Bernoulli, que la llamó Spira mirabilis «la espiral maravillosa». D'Arcy Thompson le dedicó un capítulo de su tratado On Growth and Form«Sobre crecimiento y forma» (1917).

Bernoulli escogió la figura de la espiral logarítmica como emblema y el epitafio en latín Eadem mutata resurgo ("Mutante y permanente, vuelvo a resurgir siendo el mismo") para su tumba; contrariamente a su deseo de que fuese tallada una espiral logarítmica (constante en el crecimiento de su radio), la espiral que tallaron los maestros canteros en su tumba fue una espiral de Arquímedes (constante en la diferencia de los radios). [1] La espiral logarítmica se distingue de la espiral de Arquímedes por el hecho de que las distancias entre su brazos se incrementan en progresión geométrica, mientras que en una espiral de Arquímedes estas distancias son constantes.

Eadem mutata resurgo y la espiral logarítmica es también el emblema del Colegio de Patafísica.^[1]

Jakob Bernoulli escribió que la espiral logarítmica puede ser utilizada como un símbolo, bien de fortaleza y constancia en la adversidad, o bien como símbolo del cuerpo humano, el cual, después de todos los cambios y mutaciones, incluso después de la muerte, será restaurado a su Ser perfecto y exacto. [2] (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).

Ecuaciones

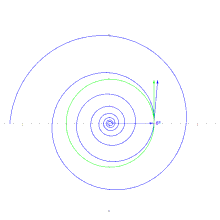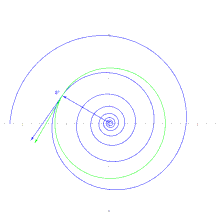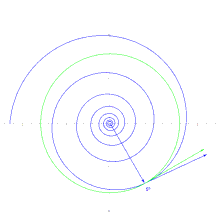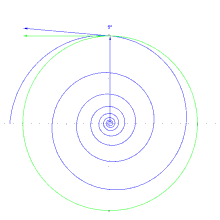
En coordenadas polares (r, θ) la fórmula de la curva puede escribirse como

r=ab^{\theta }\,

o bien

\theta =\log _{b}(r/a)\,

, de aquí el nombre "logarítmica"

y en forma paramétrica como

x(\theta )=ab^{\theta }\cos(\theta )\,

y(\theta )=ab^{\theta }\operatorname {sen}(\theta )\,

con números reales positivos a y b. a es un factor de escala que determina el tamaño de la espiral, mientras b controla cuan fuerte y en que dirección está enrollada. Para |b| >1 la espiral se expande con un incremento θ, y para |b| <1 se contrae.

En geometría diferencial, la espiral puede definirse como una curva c(t) con un ángulo constante α entre el radio y el vector tangente

\arccos {\frac {\langle \mathbf {c} (t),\mathbf {c} '(t)\rangle }{\|\mathbf {c} (t)\|\|\mathbf {c} '(t)\|}}=\alpha

Si α = 0 la espiral logarítmica degenera en una línea recta.

Si α = ± π / 2 la espiral logarítmica degenera en una circunferencia.

Características

Espiral construida utilizando rectángulos con la proporción áurea. Resulta una aproximación a la espiral logarítmica.

Cualquier línea recta al origen cortará a la espiral logarítmica con el mismo ángulo α, que puede calcularse (en radianes) como arctan(1/ln(b)). El grado de la espiral es el ángulo (constante) que la espiral posee con circunferencias centradas en el origen. Puede calcularse como arctan(ln(b)). Una espiral logarítmica de grado 0 (b = 0) es una circunferencia; el caso límite es una espiral logarítmica de grado 90 (b = 0 o b = ∞) es una línea recta desde el origen.

Comenzando en un punto P y moviéndose hacia dentro, a lo largo de la espiral, hay que rodear el origen infinitas veces antes de alcanzarlo; sin embargo, la distancia total de este camino es finita. El primero en darse cuenta de esto fue Torricelli incluso antes de que se ideara el cálculo infinitesimal. La distancia total es r/cos(α), donde r es la distancia en línea recta desde P al origen.

Se pueden construir espirales logarítmicas de grado 17,03239 utilizando la sucesión de Fibonacci o la proporción áurea.

La espiral logarítmica se distingue de la espiral de Arquímedes por el hecho de que las distancias entre su brazos se incrementan en progresión geométrica, mientras que en una espiral de Arquímedes estas distancias son constantes.

Espirales logarítmicas en la naturaleza

Los brazos de las galaxias espirales son aproximadamente espirales logarítmicas. Nuestra propia galaxia, la Vía Láctea, se cree que tiene cuatro brazos espirales mayores, cada uno de los cuales es una espiral logarítmica de unos 12 grados.

Los brazos de los ciclones tropicales, como los huracanes, también forman espirales logarítmicas.

En biología son frecuentes las estructuras aproximadamente iguales a la espiral logarítmica. Por ejemplo, las telas de araña y las conchas de molusco. La razón es la siguiente: comienza con una figura irregular F₀. Se aumenta F₀ en un cierto factor para obtener F₁, y se pone F₁ junto a F₀, de forma que se toquen dos lados. Se aumenta F₁ en el mismo factor para obtener F₂, y se pone junto a F₁, como antes. Repitiendo este proceso se genera aproximadamente una espiral logarítmica cuyo grado está determinado por el factor de expansión y el ángulo con que las figuras son puestas una al lado de otra.

El halcón se aproxima a su presa según una espiral logarítmica: su mejor visión está en ángulo con su dirección de vuelo; este ángulo es el mismo que el grado de la espiral.

Los insectos se aproximan a las luces artificiales según una espiral aproximadamente logarítmica, porque están acostumbrados a volar con un ángulo constante a las fuentes luminosas. Normalmente son el Sol o la Luna la única fuente de luz y volar de esta forma produce un vuelo en línea recta, ya que el insecto no hace vuelos tan largos como para que la posición del Sol o la Luna cambie significativamente.

En geotecnia, la superficie de falla es el lugar geométrico de los puntos en donde el suelo "se rompe" y permite un deslizamiento, al estar sometido a cargas mayores a la que puede soportar. Estas superficies de falla en muchos casos son iguales o aproximables a una espiral logarítmica.

Y, también en los girasoles, se encuentran repetidas espirales logarítmicas.

Galería

$Fracción de un fractal Mandelbrot.$

Fracción de un fractal Mandelbrot.
Imagen de la Galaxia de Bode (M81) por el Telescopio Espacial Spitzer, en la que se puede observar polvo interestelar siguiendo aproximadamente una espiral logarítmica.
Ciclón Catarina, un infrecuente ciclón tropical del Atlántico Sur visto desde la Estación Espacial Internacional. Tiene unos unos brazos que se aproximan a la forma de una espiral logarítmica.
Una borrasca sobre Islandia. El patrón que sigue se aproxima a la forma de una espiral logarítmica.
Corte de la concha de un nautilus donde se aprecian las cámaras formando aproximadamente una espiral logarítmica.
El símbolo de Debian se parece a una espiral logarítmica.