Distribución estable

Distribuciones estables
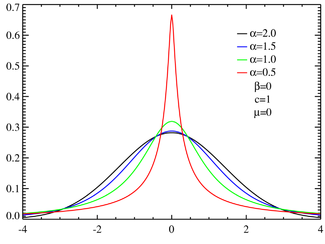Distribución α-estable simétrica con factor de escala unitario 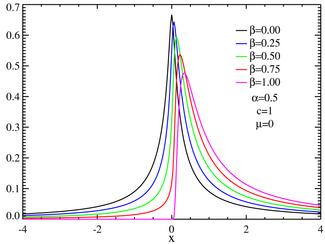Distribuciones estables asimétricas centradas con factor de escala unitario Función de densidad de probabilidad
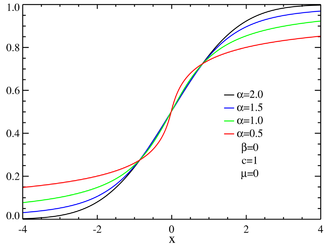Función de distribución para las distribuciones α-estables simétricas 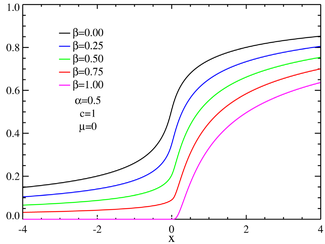Función de distribución para distribuciones estables asimétricas Función de distribución de probabilidad
Parámetros	α ∈ (0, 2] — parámetro de estabilidad β ∈ [−1, 1] — parámetro de asimetría (nótese que la asimetría no está definida) c ∈ (0, ∞) — parámetro de escala μ ∈ (−∞, ∞) — parámetro de localización
Dominio	x ∈ R, o x ∈ [μ, +∞) si α < 1 y β = 1, o x ∈ (-∞, μ] si α < 1 y β = −1
Función de densidad (pdf)	no hay forma analítica explícita, excepto para algunos valores de los parámetros
Función de distribución (cdf)	no hay forma analítica explícita, excepto para algunos valores de los parámetros
Media	μ cuando α > 1 y no definida en el resto de casos
Mediana	μ cuando β = 0 y no definida en el resto de casos
Moda	μ cuando β = 0 y no definida en el resto de casos
Varianza	2c2 cuando α = 2, para otros casos no es finita
Coeficiente de simetría	0 cuando α = 2, para otros casos no es finita
Curtosis	0 when α = 2, para otros casos no es finita
Entropía	no hay forma analítica explícita, excepto para algunos valores de los parámetros
Función generadora de momentos (mgf)	no definida
Función característica	$\exp \!{\Big [}\;it\mu -|c\,t|^{\alpha }\,(1-i\beta \,{\mbox{sgn}}(t)\Phi )\;{\Big ]},$ donde $\Phi ={\begin{cases}\tan {\tfrac {\pi \alpha }{2}}&{\text{if }}\alpha \neq 1\\-{\tfrac {2}{\pi }}\log |t|&{\text{if }}\alpha =1\end{cases}}$

En teoría de la probabilidad, una distribución se denomina estable (o una variable aleatoria se denomina estable) si es una combinación lineal de dos o más copias independientes de una muestra aleatoria que tiene la misma distribución de probabilidad, salvo por quizá algún parámetro de localización o escala.

La familia de distribuciones estables a veces se denomina también distribución α-estable de Lévy, en honor a Paul Lévy, el primero en estudiar este tipo de distribuciones.​​

De los cuatro parámetros que definen una distribución estable, el más significativo es el parámetro de estabilidad, α (ver ficha lateral). Las distribuciones estables satisfacen que 0 < α ≤ 2, correspondiendo el valor máximo con una distribución normal (que es el caso más sencillo de distribución estable). El valor α = 1 corresponde a la distribución de Cauchy. Las distribuciones estables no tienen una varianza finita si α < 2, más aún si α ≤ 1 ni siquiera tienen media finita. La importancia práctica de las distribuciones estables es que son "atractores" para la distribución de sumas de variables aleatorias independientes e idénticamente distribuidas (que además pertenecen a espacios Lp). La distribución normal define una subfamilia de distribuciones estables. Por el clásico teorema del límite central la suma de un conjunto de variables con idéntica distribución e independientes y que además tenga varianza finita, tenderá a una distribución normal a medida que el número de variables que interviene en la suma crece. Sin la restricción de varianza finita, el teorema del límite central no será aplicable, pero la suma de esas variables tenderá hacia una distribución estable (α < 2).

Mandelbrot denominó a las distribuciones estables con α < 2 como "distribuciones estables paretianas",​​​ por Vilfredo Pareto. Mandelbrot usó el término para distribuciones estables "positivas" (es decir, máximamente asimétricas hacia la dirección positiva) con 1<α<2 como "distribuciones de Pareto-Lévy".​ Además consideró que estas últimas eran relevantes para describir los precios de acciones y productos de consumo.

Definición

Una distribución no degenerada es estable si satisface la siguiente propiedad:

Sean X₁ y X₂ dos copias de una variable aleatoria X (es decir, dos instancias de variables aleatorias independientes, de variables que tienen la misma distribución que X). Entonces X se denomina estable si existen dos constantes a > 0 y b > 0 tales que la nueva variable aleatoria aX₁ + bX₂ tenga la misma distribución que cX + d para otras dos constantes c > 0 y d. La distribución se llama estictamente estable si esto sigue siendo cierto aún con d = 0.​

Puesto que la distribución normal, la distribución de Cauchy y la distribución de Lévy satisfacen esta propiedad, son casos particulares de distribuciones estables. Más aún, Lévy demostró que el conjunto de todas las distribuciones estables puede representarse como una familia dada por cuatro parámetros de distribuciones continuas. Dos de los parámetros representan el parámetro de localización μ y el factor de escala c, mientras que los otros dos β y α, se corresponden con el grado de asimetría y concentración (ver gráficas de la ficha lateral).

Aunque la densidad de probabilidad de estas distribuciones estables no admite una fórmula analítica cerrada (expresable en términos de funciones elementales), sin embargo, su función característica si admite una fórmula analítica cerrada. Cualquier distribución de probaiblidad dada por la transformada de Fourier de una función característica φ(t) del tipo:

$f(x)={\frac {1}{2\pi }}\int _{-\infty }^{\infty }\varphi (t)e^{-ixt}\,dt$

Una variable aleatoria X es estable si su función característica puede escribirse como​​

$\varphi (t;\alpha ,\beta ,c,\mu )=\exp \left[~it\mu \!-\!|ct|^{\alpha }\,(1\!-\!i\beta \,{\textrm {sgn}}(t)\Phi )~\right]$

donde sgn(t) es simplemente la función signo de t y Φ viene dada por

$\Phi =\tan(\pi \alpha /2)\,$

para todo α, excepto α = 1, en cuyo caso:

$\Phi =-{\frac {2}{\pi }}\log |t|.\,$

μ ∈ R es un parámetro de localización y β ∈ [−1, 1] se denomina parámetro de asimetría. Nótese que en este contexto la asimetría "usual" no está bien definida, cuando α < 2 ya que la distribución no admite moments de segundo orden ni superiores (pero la asimetría usual usa en su definición el tercer momento central).

La razón de que una distribución que satisface las condiciones anteriores sea estable es que la función característica para la suma de dos variables aleatorias es igual al producto de las correspondientes funciones características. Al sumar dos variables aleatorias que tienen una distribución estable se obtiene otra variable con los mismos valores de α y β, pero posiblemente valores diferentes de μ y c (cambia la localización y la escala, pero no la el parámetro de estabilidad ni el parámetro de asimetría).

No cualquier función es la función característica de una distribución de probabilidad legítima, ya que una función de distribución real varía entre 0 y 1 son decrecer, pero la función caractecterística dada anteriormente podría no ser adecuada si los pámetros no están dentro del rango adecuado. El valor de la función característica para cierto valor t es el complejo conjugado de su valor en −t como debería ser para que una función de distribución sea real. En el caso más sencillo β = 0, la función característica es simplemente una función exponencial estirada, la distribución es simétrica alrededor de μ y en ese caso se denomina distribución α-estable simétrica de Lévy, frecuentemente abreviada como SαS. Cuando α < 1 y β = 1, la distribución tiene un soporte en [μ, ∞). El parámetro c > 0 es un factor de escala que mide el ancho típico de la distribución mientras que α es el exponente o índice de la distribución que especifica el comportamiento asintótico de dicha distribución.

Referencias

Enlaces externos

• The STABLE program for Windows is available from John Nolan's stable webpage: http://academic2.american.edu/~jpnolan/stable/stable.html Archivado el 30 de octubre de 2006 en Wayback Machine.. It calculates the density (pdf), cumulative distribution function (cdf) and quantiles for a general stable distribution, and performs maximum likelihood estimation of stable parameters and some exploratory data analysis techniques for assessing the fit of a data set.
• Matlab codes for simulation of stable variables and estimation of stable parameters are available from RePEc: https://ideas.repec.org/e/pwe42.html#software

• Datos: Q1934245