Discusión:Límite de una función

EN TRADUCCIÓN

Contenido en traducción

Definición formal La imagen de ejemplo tiene pinta de estar dibujada con Paint. Alguien puede editar otra con Matlab, Maple, Derive...? Límite de una función en un punto Algunas veces, el límite también se define considerando valores de x distintos de p (lo que sería un límite relativo usando la definición dada -i.e., un límite considerando una restricción del dominio-). Para esta definición se tiene que: $\lim _{x\to p}f(x)=L\Leftrightarrow \forall _{\varepsilon >0}\exists _{\delta >0}\forall _{x\in \mathbb {D} }\ 0<|x-p|<\delta \Rightarrow |f(x)-L|<\varepsilon$ esto es un caso particular de funciones en espacios métricos en los que tanto M como N son números reales. O escribimos: $\lim _{x\to p}f(x)=\infty$ sí y sólo si para cada R > 0 existe un δ > 0 tal que para todos los números reales x con 0 < |x-p| < δ, se obtiene que f(x) > R; O escribimos: $\lim _{x\to p}f(x)=-\infty$ sí y sólo si para cada R < 0 existe un δ > 0 tal que para cualquier número real x with 0 < |x-p| < δ, se obtiene que f(x) < R. Esta definición se puede simplificar usando el concepto de Proximidad, que también permite expresiones como $\lim _{x\to +\infty }f(x)=L$. Escribimos: $\lim _{x\to p}f(x)=L$ donde: $x\in {\overline {\mathbb {D} }}$ y $p;L\in {\tilde {\mathbb {R} }}$ sí y sólo si $\forall _{\varepsilon >0}\exists _{\delta >0}\forall _{x\in \mathbb {D} }\ x\in B_{\delta }(p)\Rightarrow f(x)\in B_{\varepsilon }(L)$ Si, en las definiciones se utiliza x-p en lugar de |x-p|, entonces tenemos el límite lateral por la derecha, cuya notación es limx→p+. Si se utiliza p-x, entonces se tiene el límite lateral por la izquierda, cuya notación es limx→p-. Consultar la entrada principal one-sided limit. ... Sometimes, the limit is also defined considering for x values different from p. (which would be a relative limit - that is, a limit considering a restriction to the domain - using the already given definition). For such definition we have: $\lim _{x\to p}f(x)=L\Leftrightarrow \forall _{\varepsilon >0}\exists _{\delta >0}\forall _{x\in \mathbb {D} }\ 0<|x-p|<\delta \Rightarrow |f(x)-L|<\varepsilon$ It is just a particular case of functions on metric spaces, with both M and N are the real numbers. Or we write $\lim _{x\to p}f(x)=\infty$ if and only if for every R > 0 there exists a δ > 0 such that for all real numbers x with 0 < |x-p| < δ, we have f(x) > R; or we write $\lim _{x\to p}f(x)=-\infty$ if and only if for every R < 0 there exists a δ > 0 such that for all real numbers x with 0 < |x-p| < δ, we have f(x) < R. This definition can be condensed by using the concept of Neighbourhood, which also allows expressions such as $\lim _{x\to +\infty }f(x)=L$. We write $\lim _{x\to p}f(x)=L$ (where $x\in {\overline {\mathbb {D} }}$ and $p;L\in {\tilde {\mathbb {R} }}$) if and only if $\forall _{\varepsilon >0}\exists _{\delta >0}\forall _{x\in \mathbb {D} }\ x\in B_{\delta }(p)\Rightarrow f(x)\in B_{\varepsilon }(L)$ If, in the definitions, x-p is used instead of |x-p|, then we get a right-handed limit, denoted by limx→p+. If p-x is used, we get a left-handed limit, denoted by limx→p-. See main article one-sided limit. Limit of function at infinity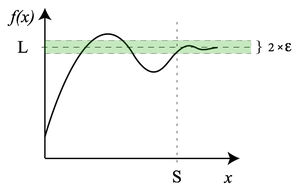 Limit of a function at infinity exists if, for every ε > 0 there exists a S > 0 ; so that |f(x)-L| < ε for all x > S. Suppose f(x) is a real-valued function. We can also consider the limit of function when x increases or decreases indefinitely. We write $\lim _{x\to \infty }f(x)=L$ if and only if for every ε > 0 there exists S >0 such that for all real numbers x>S, we have |f(x)-L|<ε or we write $\lim _{x\to \infty }f(x)=\infty$ for every R > 0 there exists S >0 such that for all real numbers x>S, we have f(x)>R. Similarly, we can define the expressions $\lim _{x\to \infty }f(x)=-\infty ,\lim _{x\to -\infty }f(x)=L,\lim _{x\to -\infty }f(x)=\infty ,\lim _{x\to -\infty }f(x)=-\infty$. There are three basic rules for evaluating limits at infinity for a rational function f(x) = p(x)/q(x): If the degree of p is greater than the degree of q, then the limit is positive or negative infinity depending on the signs of the leading coefficients If the degree of p and q are equal, the limit is the leading coefficient of p divided by the leading coefficient of q If the degree of p is less than the degree of q, the limit is 0 If the limit at infinity exists, it represents a horizontal asymptote at x = L. Polynomials do not have horizontal asymptotes; they may occur with rational functions. Complex-valued functions The complex plane with metric $d(x,y):=|x-y|$ is also a metric space. There are two different types of limits when we consider complex-valued functions. Limit of a function at a point Suppose f is a complex-valued function, then we write $\lim _{x\to p}f(x)=L$ if and only if for every ε > 0 there exists a δ >0 such that for all real numbers x with 0<|x-p|<δ, we have |f(x)-L|<ε It is just a particular case of functions over metric spaces with both M and N are the complex plane. Limit of a function at infinity We write $\lim _{x\to \infty }f(x)=L$ if and only if for every ε > 0 there exists S >0 such that for all complex numbers |x|>S, we have |f(x)-L|<ε test Limit of a function of more than one variable By noting that |x-p| represents a distance, the definition of a limit can be extended to functions of more than one variable. $\lim _{(x,y)\to (p,q)}f(x,y)=L$ if and only if for every ε > 0 there exists a δ > 0 such that for all real numbers x with 0 < ||(x,y)-(p,q)|| < δ, we have |f(x,y)-L| < ε where ||(x,y)-(p,q)|| represents the Euclidean distance. This can be extended to any number of variables.

Definiciones complejas

La definicion del tema se puede notar que esta muy complejo para un niño. Falta como menos teoria y mas ejemplos sencillos. — El comentario anterior es obra de 190.27.74.82 (disc. · contr. · bloq.), quien olvidó firmarlo. Farisori » 04:46 20 may 2009 (UTC)

Ciertamente no es un concepto accesible a un niño cualquiera, es un concepto muy profundo y con muchas sutilezas. Se puede dar una idea informal, pero rebajar el nivel general de la entrada haría que ésta contuviera ambigüedades y errores, además de que dejaría de cumplir su cometido de proporcionar la información a quienes ya están estudiando estos temas. --Usuario:drini 01:27 20 feb 2010 (UTC)

---

Buenas tardes... en el tema falto una inderminacion y es: 0(al infinito) — El comentario anterior sin firmar es obra de Qebm (disc. • contribs • bloq). Farisori » 20:57 22 nov 2010 (UTC)