Distribución de Cauchy

Cauchy-Lorentz
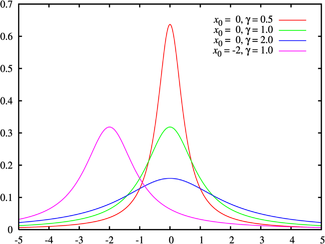	; La línea verde es la distribución estándar de Cauchy; Función de densidad de probabilidad
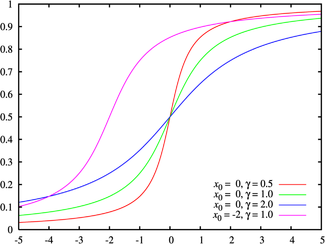	; Leyenda de colores para la PDF de la imagen superior; Función de distribución de probabilidad
Parámetros	(real); escala (real)
Función de densidad (pdf)
Función de distribución (cdf)
Media	no definida
Mediana
Moda
Varianza	no definida
Curtosis	no definida
Entropía
Función generadora de momentos (mgf)	no definida
Función característica
	[editar datos en Wikidata]

La distribución Cauchy-Lorentz, llamada en honor a Augustin Cauchy y Hendrik Lorentz, es una distribución de probabilidad continua. Es conocida como la distribución de Cauchy y en el ámbito de la física se conoce como la distribución de Lorentz, la función Lorentziana ó la distribución de Breit-Wigner. Su importancia en la física es dada por ser la solución de la ecuación diferencial que describe la resonancia forzada. En espectroscopia describe la forma de las líneas espectrales que son ampliadas por diversos mecanismos, en particular, el mecanismo de ensanchamiento por colisión.

Caracterización

Función de densidad (PDF)

En estadística la distribución de Cauchy (a veces también distribución de Lorentz) es una distribución de probabilidad continua cuya función de densidad es

{\begin{aligned}f(x;x_{0},\gamma )&={\frac {1}{\pi \gamma \left[1+\left({\frac {x-x_{0}}{\gamma }}\right)^{2}\right]}}\\[0.5em]&={1 \over \pi }\left[{\gamma  \over (x-x_{0})^{2}+\gamma ^{2}}\right]\end{aligned}}

donde x₀ es el parámetro de corrimiento que especifica la ubicación del pico de la distribución, y γ es el parámetro de escala que especifica el ancho medio al máximo medio (half-width at half-maximum, HWHM).

En el caso especial donde x₀ = 0 y γ = 1 es denominado la distribución estándar Cauchy con la función de densidad de probabilidad

f(x;0,1)={\frac {1}{\pi (1+x^{2})}}.\!

En general la distribución de Cauchy no tiene valor esperado ni varianza.

Sean $U$ y $V$ dos variables aleatorias uniformes dentro -1 y 1 y $U^{2}+V^{2}<1$ , entonces el número $U/V$ tiene la distribución Cauchy.

Función de distribución

La función de distribución acumulativa (CDF) es:

F(x;x_{0},\gamma )={\frac {1}{\pi }}\arctan \left({\frac {x-x_{0}}{\gamma }}\right)+{\frac {1}{2}}

y la función inversa de distribución acumulativa para la distribución Cauchy es

F^{-1}(p;x_{0},\gamma )=x_{0}+\gamma \,\tan \left[\pi \,\left(p-{\tfrac {1}{2}}\right)\right].

Propiedades

La distribución de Cauchy es un ejemplo de una distribución que no tiene valor esperado, varianza o momentos definidos. Su moda y su mediana están bien definidas y son ambas iguales a x₀.

Cuando U y V son dos variables aleatorias independendientes y normalmente distribuidas con un valor esperado = 0 y una variancia = 1, luego la tasaU/V tiene la distribución estándar de Cauchy.

Sí X₁, …, X_n son variables aleatorias, independientes e idénticamente distribuidas, cada una con una distribución Cauchy, luego la media de la muestra (X₁ + … + X_n)/n tiene la misma distribución Cauchy estándar (la media de la muestra, la cuál no es afectada por los valores extremos, puede ser usada como medida de la tendencia central). Para comprobar que esto es cierto se calcula la función característica de la media de la muestra:

\phi _{\overline {X}}(t)=\mathrm {E} \left(e^{i\,{\overline {X}}\,t}\right)\,\!

donde ${\overline {X}}$ es la media de la muestra. Este ejemplo sirve para demostrar que la hipótesis de variancia finita en el teorema del límite central no puede ser depuesta, al igual que la hipótesis de esperanza finita en la ley de los grandes números. Es también un ejemplo de una versión más generalizada del teorema de límite central que es característica de todas las distribuciones asimétricas alpha-estables de Lévy, de las cuales es la distribución de Cauchy un caso especial.

La distribución de Cauchy es una función de distribución infinitamente divisible. Es también una distribución estrictamente estable.

La distribución de Cauchy coíncide con la distribución t de Student con un grado de libertad.

Función Característica

Sea X una variable aleatoria con una distribución Cauchy. Luego la función característica de la distribución Cauchy está bien definida:

\phi _{x}(t;x_{0},\gamma )=\mathrm {E} (e^{i\,X\,t})=\exp(i\,x_{0}\,t-\gamma \,|t|).\!

Enlaces externos