Numeración indo-arábiga

Los números arábigos son los símbolos más utilizados para representar números. Se les llama "arábigos" porque los árabes los introdujeron en Europa, aunque en realidad son invención de los indios. El mundo le debe a la cultura india el invento trascendental del sistema de numeración de base 10, llamado de posición, así como el descubrimiento del 0 (llamado "sunya" o "bindu" en lengua sánscrita), aunque los mayas también conocieron el 0; también los mayas preclásicos (o sus predecesores olmecas) desarrollaron independientemente el concepto de cero alrededor del año 36 AC. Un documento datado en esa fecha es el primer uso documentado de un cero como lo conocemos hoy en día; es decir que los olmecas parecen haber estado usando el concepto de cero siglos antes que en el viejo mundo. sin embargo los mayas usaban el cero en un sistema "vigesimal", muy distinto al que utilizamos.

El sistema numérico llamado "arábigo" es un sistema posicional que se basa en el número 10; consta de 10 glifos diferentes para representar los 10 dígitos. El valor de un dígito varía según la posición que ocupa dentro del número mutiplicándose por la base elevado a la posición. Así, el primer dígito comenzando por la derecha tiene el valor que representa su símbolo multiplicado por $10^{0}$(=1). El dígito situado a su izquierda tiene el valor que representa su símbolo multiplicado por $10^{1}$(=10), y así sucesivamente. La fórmula genérica para un número de $n$ dígitos es $\sum _{i=1}^{n}x_{i}\cdot 10^{(i-1)}$ donde $x_{i}$ es el dígito situado en la posición $i$ comenzando por la derecha. Por ejemplo:

$''639''=(6\cdot 10^{2})+(3\cdot 10^{1})+(9\cdot 10^{0})=$ $(6\cdot 100)+(3\cdot 10)+(9\cdot 1)=600+30+9=639$

El sistema "arábigo" se ha representado (y se representa) utilizando muchos conjuntos de glifos diferentes. Estos glifos pueden dividirse en dos grandes familias, los numerales arábigos occidentales y los orientales. Los orientales, que se desarrollaron en lo que actualmente se corresponde a Irak, se representan en la tabla que viene a continuación como Arábigo-Índico. El Arábigo-Índico oriental es una variedad de los glifos arábigo-índicos. Los numerales arábigos occidentales, desarrollados en Al-Ándalus y el Magreb se muestran en la tabla como Europeo

Europeo	0	1	2	3	4	5	6	7	8	9
Arábico-Índico	٠	١	٢	٣	٤	٥	٦	٧	٨	٩
Arábico-Índico Oriental (Persa y Urdu)	۰	۱	۲	۳	۴	۵	۶	۷	۸	۹
Devanagari (Hindi)	०	१	२	३	४	५	६	७	८	९
Tamil		௧	௨	௩	௪	௫	௬	௭	௮	௯

En Japón, los números "arábigos" y el alfabeto latino forman parte del sistema de escritura rōmaji. Así, si un número está escrito con glifos "arábigos", en Japón dirán que “está escrito en rōmaji” en contraposición a la numeración japonesa.

Historia

El sistema de numeración arábigo se considera uno de los avances más significativos de las matemáticas. La mayoría de los historiadores coinciden en afirmar que tuvo su origen en la India (los árabes se refieren a este sistema de numeración como “Números Indios”, أرقام هندية, arqam hindiyyah), y se expandió por el mundo islámico y de ahí, vía al-Andalus, al resto de Europa.

Se especula que el origen del sistema posicional base 10 utilizado en la India tuviera sus orígenes en China. El sistema chino Hua Ma (ver Numeración china) es también posicional y de base 10 y pudo haber servido de inspiración para el sistema que surgió en la India. Esta hipótesis cobra fuerza por el hecho de que entre los siglos V y VIII (periodo durante el cual se desarrolló el sistema numérico indio) coincidió con una gran afluencia de peregrinos budistas entre China y la India. Lo que es cierto es que en la época de Bhaskara I (Siglo VII) en la India se utilizaba un sistema numeral posicional base 10 con 9 glifos, y se conocía el concepto del cero, representado por un punto.

Este sistema de numeración llegó a Oriente Medio hacia el año 670. Matemáticos musulmanes del actual Iraq, como al-Jwarizmi, ya estaban familiarizados con la numeración babilónica, que utilizaba el cero entre dígitos distintos de cero (aunque no tras dígitos distintos de cero), así que el nuevo sistema no tuvo una difícil acogida. En el siglo X los matemáticos árabes incluyeron en su sistema de numeración las fracciones.

Tabela com "apices" na Idade Média

Table of numerals

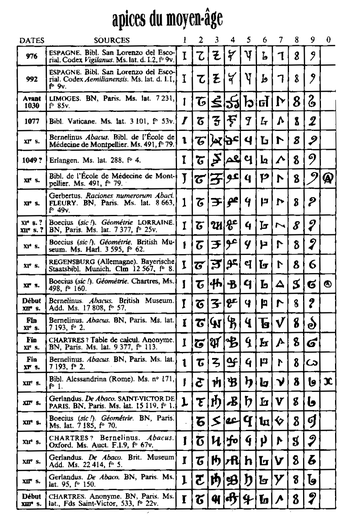Fibonacci, un matemático italiano que había estudiado en Bejaia (en la actual Argelia), contribuyó a la difusión por Europa del sistema arábigo con su libro Liber Abaci, publicado en 1202. Sin embargo no fue hasta la invención de la imprenta cuando este sistema de numeración comenzó a utilizarse de forma generalizada.

Curiosamente, hasta tiempos relativamente recientes, en el mundo musulmán solamente los matemáticos utilizaban el sistema de numeración arábigo. Los científicos utilizaban el sistema babilónico y los comerciantes los sistemas griego y hebreo.