Diferencia entre revisiones de «Ángulos suplementarios»
Apariencia
Contenido eliminado Contenido añadido
Sin resumen de edición |
m Revertidos los cambios de 190.99.189.254 a la última edición de AVBOT |
||
| Línea 1: | Línea 1: | ||
[[Imagen:Angulos_suplementarios.png|right|180px|Ángulos suplementarios.]] |
[[Imagen:Angulos_suplementarios.png|right|180px|Ángulos suplementarios.]] |
||
Dos '''ángulos suplementarios''' son aquellos cuya suma de medidas es |
Dos '''ángulos suplementarios''' son aquellos cuya suma de medidas es 180º ([[grado sexagesimal|grados sexagesimales]]). |
||
Así, para obtener el [[ángulo]] suplementario de '''α''', que tiene una amplitud de 120°, se restará '''α''' de 180°: |
Así, para obtener el [[ángulo]] suplementario de '''α''', que tiene una amplitud de 120°, se restará '''α''' de 180°: |
||
| Línea 9: | Línea 9: | ||
* 360 grados sexagesimales equivalen a 2π [[radián|radianes]], o 400 [[grado centesimal|grados centesimales]]. |
* 360 grados sexagesimales equivalen a 2π [[radián|radianes]], o 400 [[grado centesimal|grados centesimales]]. |
||
=== |
=== Propiedades === |
||
putas Propiedades === |
|||
Si dos ángulos son suplementarios de otros dos [[ángulos congruentes]], también son congruentes entre sí. |
Si dos ángulos son suplementarios de otros dos [[ángulos congruentes]], también son congruentes entre sí. |
||
Revisión del 16:41 5 ene 2010
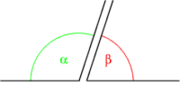
Dos ángulos suplementarios son aquellos cuya suma de medidas es 180º (grados sexagesimales).
Así, para obtener el ángulo suplementario de α, que tiene una amplitud de 120°, se restará α de 180°:
- β = 180° – 120º = 60º
- 360 grados sexagesimales equivalen a 2π radianes, o 400 grados centesimales.
Propiedades
Si dos ángulos son suplementarios de otros dos ángulos congruentes, también son congruentes entre sí.
Véase también
Otras relaciones aritméticas entre ángulos:
Relaciones posicionales entre ángulos:
