Формула трубки: различия между версиями
Перейти к навигации
Перейти к поиску
| [отпатрулированная версия] | [отпатрулированная версия] |
Содержимое удалено Содержимое добавлено
Tosha (обсуждение | вклад) |
Tosha (обсуждение | вклад) |
||
| (не показано 48 промежуточных версий 4 участников) | |||
| Строка 1: | Строка 1: | ||
[[Файл:Voisinage tubulaire.svg|right|thumb|Кривая и её трубчатая окрестность.]] |
|||
'''Формула трубки''' или '''формула Вейля''' — выражение для |
'''Формула трубки''' или '''формула Вейля''' — выражение для объёма <math>r</math>-окрестности подмногообразия как многочлен от <math>r</math>. |
||
Предложена [[Вейль, Герман|Германом Вейлем]]. |
Предложена [[Вейль, Герман|Германом Вейлем]]. |
||
==Формулировка== |
==Формулировка== |
||
Пусть <math>M</math> замкнутое <math>m</math>-мерное подмногообразие в <math>n</math>-мерном |
Пусть <math>M</math> замкнутое <math>m</math>-мерное подмногообразие в <math>n</math>-мерном евклидовом пространстве, |
||
соответственно <math>k=n-m</math> есть [[коразмерность]] <math>M</math>. |
|||
Обозначим через <math>M_r</math> <math>r</math>-окрестность <math>M</math>. |
Обозначим через <math>M_r</math> <math>r</math>-окрестность <math>M</math>. |
||
Тогда для всех достаточно малых положительных значений <math>r</math> выполняется равенство |
|||
:<math>V(M_r)=\sum_{m\ |
:<math>V(M_r)=\omega_{k}\cdot r^{k}\cdot\sum_{m\ge 2\cdot i\ge 0}V_i(M)\cdot \frac{r^{2\cdot i}}{k\cdot(k+2)\cdots(k+2\cdot i)},</math> |
||
где |
где |
||
<math>V(M_r)</math> — объём <math>M_r</math> и |
<math>V(M_r)</math> — объём <math>M_r</math>, <math>\omega_k</math> — объём единичного шара в <math>k</math>-мерном евклидовом пространстве. и |
||
:<math>V_i |
:<math>V_i(M)=\int\limits_M p_i(\mathrm{Rm})</math> |
||
для некоторого однородного многочлена <math>p_i</math> степени <math>i</math> |
для некоторого [[однородный многочлен|однородного многочлена]] <math>p_i</math> степени <math>i</math>; здесь <math>\mathrm{Rm}</math> обозначает [[тензор кривизны]]. |
||
Выражение <math>p_i(\mathrm{Rm})</math> это так называемая '''кривизна Липшица — |
Выражение <math>p_i(\mathrm{Rm})</math> — это так называемая '''кривизна Липшица — Киллинга''', |
||
она |
она пропоциональна среднему [[пфафиан]]у тензора кривизны по всем <math>(2\cdot i)</math>-мерным подпространствам касательного пространства. |
||
===Замечания=== |
===Замечания=== |
||
*<math>V_0</math> |
*Младший ненулевой коэффициент <math>V_0(M)</math> есть <math>m</math>-мерный объём <math>M</math>. |
||
*Если размерность <math>M</math> чётна, <math>m=2\cdot k</math>, то |
*Если размерность <math>M</math> чётна, <math>m=2\cdot k</math>, то |
||
*:<math> |
*:<math>V_k=\chi(M),</math> |
||
:где <math>\chi(M),</math> — [[эйлерова характеристика]] <math>M</math> |
:где <math>\chi(M),</math> — [[эйлерова характеристика]] <math>M</math>. |
||
==Следствия== |
==Следствия== |
||
*Объём <math>r</math>-окрестности <math>\gamma_r</math> простой замкнутой гладкой кривой <math>\gamma</math> в <math>n</math>-мерном евклидовом пространстве при малых <math>r</math> выражается формулаой |
|||
*:<math>V(\gamma_r)=L(\gamma)\cdot r^{n-1},</math> |
|||
:где <math>L(\gamma)</math> обозначает длину <math>\gamma</math>. |
|||
*Для гладких замкнутой поверхности <math>M</math> в 3-мерном евклидовом пространстве выполняется равенство |
*Для гладких замкнутой поверхности <math>M</math> в 3-мерном евклидовом пространстве выполняется равенство |
||
*:<math>V(M_r)=S(M)\cdot r+ |
*:<math>V(M_r)=S(M)\cdot r+\tfrac23\cdot \pi\cdot \chi(M)\cdot r^3.</math> |
||
*Если два подмногообразия евкидова пространства изометричны то объёмы их <math>r</math>-окрестностей совпадают для всех малых положительных <math>r</math>. |
*Если два подмногообразия евкидова пространства изометричны, то объёмы их <math>r</math>-окрестностей совпадают для всех малых положительных <math>r</math>. |
||
==Вариации и обобщения== |
|||
| ⚫ | |||
*'''Формула полутрубки''' для [[гиперповерхность|гиперповерхностей]] выражает объём односторонней <math>r</math>-окрестности <math>M_r^+</math>, она также является многочленом от <math>r</math>, но не все коэффициенты зависят от внутренней кривизны. В частности для поверхностей в трёхмерном пространстве формула полутрубки принимает вид |
|||
*:<math>V(M_r^+)=S(M)\cdot r+\biggl[\int\limits_M H\biggr]\cdot r^2+\tfrac23\cdot \pi\cdot \chi(M)\cdot r^3,</math> |
|||
:где <math>H</math> обозначает [[средняя кривизна|среднюю кривизну]]. |
|||
| ⚫ | |||
*[[Обобщённая формула Гаусса — Бонне]] |
*[[Обобщённая формула Гаусса — Бонне]] |
||
*[[Смешанный объём]] |
|||
*[[Трубчатая окрестность]] |
|||
==Литература== |
|||
*''Грей А.'' Трубки. Формула Вейля и ее обобщения, Мир, 1993. |
|||
*{{статья|автор=Hermann Weyl|заглавие=On the Volume of Tubes|ссылка=http://www.math.uchicago.edu/~shmuel/AAT-readings/Data%20Analysis%20/Tubes/Weyl,%20volume%20of%20tubes.pdf|язык=en|издание=American Journal of Mathematics|год=1939|том=61|номер=2|страницы=461—472|doi=|issn=}} |
|||
| ⚫ | |||
[[Категория:Риманова (и псевдориманова) геометрия]] |
|||
==Ссылки== |
|||
| ⚫ | |||
Текущая версия от 21:59, 20 марта 2024
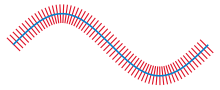
Формула трубки или формула Вейля — выражение для объёма -окрестности подмногообразия как многочлен от . Предложена Германом Вейлем.
Формулировка
[править | править код]Пусть замкнутое -мерное подмногообразие в -мерном евклидовом пространстве, соответственно есть коразмерность .
Обозначим через -окрестность . Тогда для всех достаточно малых положительных значений выполняется равенство
где — объём , — объём единичного шара в -мерном евклидовом пространстве. и
для некоторого однородного многочлена степени ; здесь обозначает тензор кривизны.
Выражение — это так называемая кривизна Липшица — Киллинга, она пропоциональна среднему пфафиану тензора кривизны по всем -мерным подпространствам касательного пространства.
Замечания
[править | править код]- Младший ненулевой коэффициент есть -мерный объём .
- Если размерность чётна, , то
- где — эйлерова характеристика .
Следствия
[править | править код]- Объём -окрестности простой замкнутой гладкой кривой в -мерном евклидовом пространстве при малых выражается формулаой
- где обозначает длину .
- Для гладких замкнутой поверхности в 3-мерном евклидовом пространстве выполняется равенство
- Если два подмногообразия евкидова пространства изометричны, то объёмы их -окрестностей совпадают для всех малых положительных .
Вариации и обобщения
[править | править код]- Формула полутрубки для гиперповерхностей выражает объём односторонней -окрестности , она также является многочленом от , но не все коэффициенты зависят от внутренней кривизны. В частности для поверхностей в трёхмерном пространстве формула полутрубки принимает вид
- где обозначает среднюю кривизну.
См. также
[править | править код]Литература
[править | править код]- Грей А. Трубки. Формула Вейля и ее обобщения, Мир, 1993.
- Hermann Weyl. On the Volume of Tubes (англ.) // American Journal of Mathematics. — 1939. — Vol. 61, no. 2. — P. 461—472.
- Simon Willerton, Intrinsic Volumes and Weyl’s Tube Formula


























![{\displaystyle V(M_{r}^{+})=S(M)\cdot r+{\biggl [}\int \limits _{M}H{\biggr ]}\cdot r^{2}+{\tfrac {2}{3}}\cdot \pi \cdot \chi (M)\cdot r^{3},}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/020b8ae2ab9a9e05f91b4edca518a96f06411c61)
