Сферическая тригонометрия

Сферическая тригонометрия — раздел тригонометрии, в котором изучаются зависимости между величинами углов и длинами сторон сферических треугольников. Применяется для решения различных геодезических и астрономических задач.

История

Основы сферической тригонометрии были заложены греческим математиком и астрономом Гиппархом во II веке до н. э. Важный вклад в её развитие внесли такие античные учёные, как Менелай Александрийский и Клавдий Птолемей. Сферическая тригонометрия древних греков опиралась на применение теоремы Менелая к полному четырёхстороннику на сфере. Древнегреческие математики излагали условие теоремы Менелая не на языке отношений синусов, а на языке отношений хорд. Для выполнения требуемых расчётов применялись таблицы хорд, аналогичные последующим таблицам синусов.

Как самостоятельная дисциплина сферическая тригонометрия сформировалась в работах средневековых математиков стран ислама. Наибольший вклад в её развитие в эту эпоху внесли такие учёные, как Сабит ибн Корра, Ибн Ирак, Кушьяр ибн Лаббан, Абу-л-Вафа, ал-Бируни, Джабир ибн Афлах, ал-Джайяни, Насир ад-Дин ат-Туси. В их работах были введены основные тригонометрические функции, сформулирована и доказана сферическая теорема синусов и ряд других теорем, применявшихся в астрономических и геодезических расчётах, ведено понятие полярного треугольника, позволявшее вычислять стороны сферического треугольника по трём его данным углам.

История сферической тригонометрии в Европе связана с трудами таких учёных, как Региомонтан, Николай Коперник, Франческо Мавролико.

Основные соотношения

Сферический треугольник.

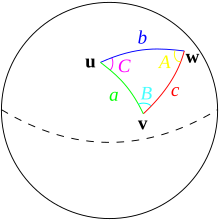
Обозначим стороны сферического треугольника a, b, c, противолежащие этим сторонам углы — A, B, C. Сторона сферического треугольника равна углу между двумя лучами исходящими из центра сферы в соответствующие концы стороны треугольника. Для радианной меры угла:

$a={\frac {|uv|}{R}},$ $b={\frac {|uw|}{R}},$ $c={\frac {|vw|}{R}}$

При использовании угла вместо длины дуги для измерения сторон сферического треугольника упрощаются формулы — в них тогда не входит радиус сферы. Так же поступают, например, в сферической астрономии, где радиус небесной сферы не имеет значения.

Теоремы для прямоугольного сферического треугольника

Пусть угол C — прямой. Тогда имеют место следующие соотношения:

$\operatorname {tg} b=\operatorname {tg} c\cos A,$

$\operatorname {tg} a=\sin b\operatorname {tg} A,$

$\sin a=\sin c\sin A,$

$\operatorname {cos} c=\operatorname {ctg} A\operatorname {ctg} B,$

$\cos A=\cos a\sin B.$

Теоремы для произвольного сферического треугольника

Сферические теоремы косинусов

$\cos a=\cos b\cos c+\sin b\sin c\cos A,$

$\cos A=-\cos B\cos C+\sin B\sin C\cos a.$

Сферическая теорема синусов

${\frac {\sin a}{\sin A}}={\frac {\sin b}{\sin B}}={\frac {\sin c}{\sin C}},\sin ^{2}A>0,\sin ^{2}B>0,\sin ^{2}C>0.$

Первая и вторая сферические теоремы косинусов двойственны по отношению друг к другу. Сферическая теорема синусов двойственна по отношению к самой себе.

Формула пяти элементов

$\sin a\cos C=\sin b\cos c-\cos b\sin c\cos A.$

$\sin A\cos c=\sin B\cos C+\cos B\sin C\cos a,$

Указанные две формулы так же двойственны друг к другу.

Применение

Знание формул сферической тригонометрии необходимо при решении таких задач, как, например, преобразование координат из одной системы небесных координат в другую, расчёт долготы центрального меридиана планеты Солнечной системы, разметка солнечных часов и точное направление спутниковой антенны («тарелки») на нужный спутник для приёма каналов спутникового телевидения.

См. также

• Решение треугольников
• Сферическая геометрия
• Ортодромия

Литература

• Волынский Б. А. Сферическая тригонометрия. — М.: Наука, 1977. — 136 с.
• Кранц П. Сферическая тригонометрия. — М.: ЛКИ, 2019. — 104 с.
• Матвиевская Г. П. Очерки истории тригонометрии. — Ташкент: Фан, 1990. — 160 с.
• Матвиевская Г. П. Очерки истории тригонометрии: Древняя Греция. Средневековый Восток. Позднее Средневековье.. — М.: URSS, 2020. — 160 с.
• Степанов Н. Н. Сферическая тригонометрия. — М.—Л.: ОГИЗ Гостехиздат, 1948. — 154 с.
• Янишевский С. Сферическая тригонометрия: лекции. — Казань: Университетская типография, 1859. — 97 с.

Ссылки

• Краткий справочник по сферической тригонометрии.
• Сферическая тригонометрия — статья из Большой советской энциклопедии. 
• Сферическая тригонометрия на сайте MathWorld