Эпициклоида: различия между версиями
| [непроверенная версия] | [отпатрулированная версия] |
| (не показаны 42 промежуточные версии 32 участников) | |||
| Строка 1: | Строка 1: | ||
'''Эпицикло́ида''' (от {{lang- |
'''Эпицикло́ида''' (от {{lang-grc|ὲπί}} — на, над, при и {{lang-grc2|κύκλος}} — круг, окружность) — [[плоская кривая]], образуемая фиксированной точкой [[окружность|окружности]], катящейся по внешней стороне другой окружности без скольжения<ref name="БСЭ1">{{ВТ-БСЭ1|Гипоциклоиды и эпициклоиды}}</ref>. |
||
По свидетельству Лейбница, Оле Рёмер ранее 1676 года сделал важное в практическом отношении открытие, что эпициклоидические зубцы в зубчатом колесе производят наименьшее трение. |
|||
| ⚫ | |||
== Уравнения == |
== Уравнения == |
||
| ⚫ | |||
Если центр неподвижной окружности находится в начале координат, её радиус равен <math>R</math>, радиус катящейся по ней окружности равен <math>r</math>, то эпициклоида описывается параметрическими уравнениями относительно <math>\varphi</math>: |
Если центр неподвижной окружности находится в начале координат, её радиус равен <math>R</math>, радиус катящейся по ней окружности равен <math>r</math>, то эпициклоида описывается параметрическими уравнениями относительно <math>\varphi</math>: |
||
: |
:<math>\begin{cases} |
||
x = (R + r)\cos\varphi - r\cos(\alpha+\frac{R+r}{r}\varphi) \\ |
x = (R + r)\cos\varphi - r\cos(\alpha+\frac{R+r}{r}\varphi) \\ |
||
y = (R + r)\sin\varphi - r\sin(\alpha+\frac{R+r}{r}\varphi) |
y = (R + r)\sin\varphi - r\sin(\alpha+\frac{R+r}{r}\varphi) |
||
\end{cases}</math> |
\end{cases}</math> |
||
где <math>\alpha</math> |
где <math>\alpha</math> — [[угол поворота]] точки, описывающей эпициклоиду, относительно центра подвижной окружности в момент начала движения (против часовой стрелки от оси x), <math>\varphi</math> — параметр, но фактически это угол наклона отрезка между центрами к оси <math>OX</math>. |
||
Можно ввести величину <math>\textstyle k=\frac{R}{r}</math>, тогда уравнения предстанут в виде |
Можно ввести величину <math>\textstyle k=\frac{R}{r}</math>, тогда уравнения предстанут в виде |
||
| Строка 17: | Строка 19: | ||
\end{cases}</math> |
\end{cases}</math> |
||
Величина <math>k</math> определяет форму эпициклоиды. При <math>k=1</math> эпициклоида образует [[Кардиоида|кардиоиду]], а при <math>k=2</math> |
Величина <math>k</math> определяет форму эпициклоиды. При <math>k=1</math> эпициклоида образует [[Кардиоида|кардиоиду]], а при <math>k=2</math> — [[нефроида|нефроиду]]. Если <math>k</math> — [[рациональное число|несократимая дробь]] вида <math>\frac{m}{n}</math> (<math>m,n \in \mathbb{N}</math>), то <math>m</math> — это количество [[касп|каспов]] данной эпициклоиды, а <math>n</math> — количество полных вращений катящейся окружности. Если <math>k</math> [[иррациональное число]], то кривая является незамкнутой и имеет бесконечное множество несовпадающих каспов. |
||
<gallery caption="Эпициклоиды при разных значениях параметра k:"> |
<gallery caption="Эпициклоиды при разных значениях параметра k:"> |
||
image:EpicycloidK1.gif| <math>k = 1</math> ([[кардиоида]]) |
|||
image:EpicycloidK2.gif| <math>k = 2</math> ([[нефроида]]) |
|||
image:EpicycloidK3.gif| <math>k = 3</math> |
|||
image:EpicycloidK0,75.gif| <math>k = \frac{3}{4}</math> |
|||
Image:Epicycloid 3to1.gif|<math>k = \frac{1}{3}</math> |
|||
Image:Epicycloid 2to1.gif|<math>k = 0.5 = \frac{1}{2}</math> |
|||
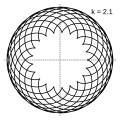
Image:Epicycloid-2-1.svg| <math>k = 2.1 = \frac{21}{10}</math> |
Image:Epicycloid-2-1.svg| <math>k = 2.1 = \frac{21}{10}</math> |
||
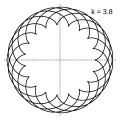
Image:Epicycloid-3-8.svg| <math>k = 3.8 = \frac{19}{5}</math> |
Image:Epicycloid-3-8.svg| <math>k = 3.8 = \frac{19}{5}</math> |
||
| Строка 30: | Строка 36: | ||
</gallery> |
</gallery> |
||
== |
== Получение == |
||
[[Image:Epizykloide herleitung.svg|thumb|255пкс|Эскиз для доказательства]] |
|||
* [http://tosamoepalevo.googlepages.com/cycloid_applet.html Java апплет, рисующий эпициклоиды с различными параметрами.] |
|||
:Пусть <math>P</math> - искомая точка, <math>\alpha</math> - угол отклонения точки <math>P</math> от точки касания двух окружностей, <math>\theta</math> - угол отклонения между центрами данных окружностей. |
|||
:Так как окружность катится без скольжения, то <math>\ell_R=\ell_r</math> |
|||
:По определению длины дуги окружности''':''' |
|||
<math>\ell_R= \theta R \and \ell_r=\alpha r</math> |
|||
:Из данных двух утверждений выплывает, что |
|||
<math>\theta R=\alpha r</math> |
|||
:Получаем соотношения для <math>\alpha</math>''':''' |
|||
<math>\alpha =\frac{R}{r} \theta</math> |
|||
:Пусть центр неподвижной окружности <math>A</math>, центр второй окружности <math>B</math>. Очевидно, что <math>\overrightarrow{AB} + \overrightarrow{BP} = \overrightarrow{AP}</math> |
|||
:Перепишем в координатах''':''' |
|||
<math>\overrightarrow{AP} = \overrightarrow{(\left( R+r \right)\cos \theta ; \left( R+r \right)\sin \theta)}+\overrightarrow{(r\cos\left( \pi + \theta+\alpha \right) ; r\sin\left( \pi + \theta+\alpha \right))} = \overrightarrow{(\left( R+r \right)\cos \theta - r\cos\left( \theta+\alpha \right);\left( R+r \right)\sin \theta - r\sin\left( \theta+\alpha \right))}</math> |
|||
Следовательно позиция точки <math>p</math>''':''' |
|||
:<math>x=\left( R+r \right)\cos \theta - r\cos\left( \theta+\alpha \right) =\left( R+r \right)\cos \theta - r\cos\left( \frac{R+r}{r}\theta \right)</math> |
|||
:<math>y=\left( R+r \right)\sin \theta - r\sin\left( \theta+\alpha \right) =\left( R+r \right)\sin \theta - r\sin\left( \frac{R+r}{r}\theta \right)</math> |
|||
== См. также == |
|||
| ⚫ | |||
{{Навигация|Викисловарь = эпициклоида|Викитека = |}} |
|||
* [[Циклоида]] |
|||
* [[Гипоциклоида]] |
|||
* [[Эпитрохоида]] |
|||
== Примечания == |
|||
{{примечания}} |
|||
{{Библиоинформация}} {{^v}} |
|||
| ⚫ | |||
{{нет ссылок|дата=5 декабря 2019}} |
|||
[[Категория:Кривые]] |
[[Категория:Кривые]] |
||
[[Категория:Трансцендентные кривые]] |
[[Категория:Трансцендентные кривые]] |
||
[[af:Episikloïed]] |
|||
[[ar:دويري فوقي]] |
|||
[[bg:Епициклоида]] |
|||
[[ca:Epicicloide]] |
|||
[[cs:Epicykloida]] |
|||
[[de:Epizykloide]] |
|||
[[en:Epicycloid]] |
|||
[[es:Epicicloide]] |
|||
[[fi:Episykloidi]] |
|||
[[fr:Épicycloïde]] |
|||
[[hu:Epiciklois]] |
|||
[[io:Epicikloido]] |
|||
[[it:Epicicloide]] |
|||
[[lmo:Epiciclòit]] |
|||
[[nl:Cycloïde#Epicycloïde]] |
|||
[[pl:Epicykloida]] |
|||
[[pms:Epissiclòida]] |
|||
[[ro:Epicicloidă]] |
|||
[[sv:Epicykloid]] |
|||
[[th:เอพิไซคลอยด์]] |
|||
[[uk:Епіциклоїда]] |
|||
[[zh:外摆线]] |
|||
Текущая версия от 04:16, 25 июля 2024
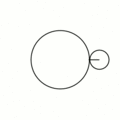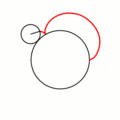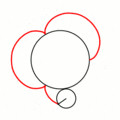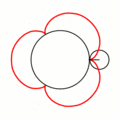
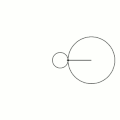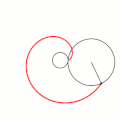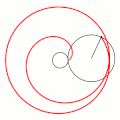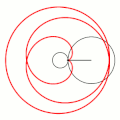
Эпицикло́ида (от др.-греч. ὲπί — на, над, при и κύκλος — круг, окружность) — плоская кривая, образуемая фиксированной точкой окружности, катящейся по внешней стороне другой окружности без скольжения[1].
По свидетельству Лейбница, Оле Рёмер ранее 1676 года сделал важное в практическом отношении открытие, что эпициклоидические зубцы в зубчатом колесе производят наименьшее трение.
Уравнения
[править | править код]
Если центр неподвижной окружности находится в начале координат, её радиус равен , радиус катящейся по ней окружности равен , то эпициклоида описывается параметрическими уравнениями относительно :
где — угол поворота точки, описывающей эпициклоиду, относительно центра подвижной окружности в момент начала движения (против часовой стрелки от оси x), — параметр, но фактически это угол наклона отрезка между центрами к оси .
Можно ввести величину , тогда уравнения предстанут в виде
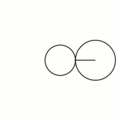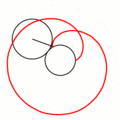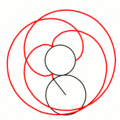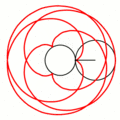
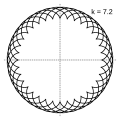
Величина определяет форму эпициклоиды. При эпициклоида образует кардиоиду, а при — нефроиду. Если — несократимая дробь вида (), то — это количество каспов данной эпициклоиды, а — количество полных вращений катящейся окружности. Если иррациональное число, то кривая является незамкнутой и имеет бесконечное множество несовпадающих каспов.
- Эпициклоиды при разных значениях параметра k:
-
(нефроида)
-
-
-
-
-
-
-
-
Получение
[править | править код]
- Пусть - искомая точка, - угол отклонения точки от точки касания двух окружностей, - угол отклонения между центрами данных окружностей.
- Так как окружность катится без скольжения, то
- По определению длины дуги окружности:
- Из данных двух утверждений выплывает, что
- Получаем соотношения для :
- Пусть центр неподвижной окружности , центр второй окружности . Очевидно, что
- Перепишем в координатах:
Следовательно позиция точки :
См. также
[править | править код]Примечания
[править | править код]- ↑ Гипоциклоиды и эпициклоиды // Большая советская энциклопедия : в 66 т. (65 т. и 1 доп.) / гл. ред. О. Ю. Шмидт. — М. : Советская энциклопедия, 1926—1947.
В статье не хватает ссылок на источники (см. рекомендации по поиску). |