C3-линеаризация: различия между версиями
| [отпатрулированная версия] | [непроверенная версия] |
Fractaler (обсуждение | вклад) м убрана категория «Объектно-ориентированное программирование»; добавлена категория «Наследование (программирование)» с помощью [[ВП:HOTCA |
РобоСтася (обсуждение | вклад) м checkwiki→ middle priority → Заголовок завершается двоеточием, replaced: : == → == (2) |
||
| (не показано 19 промежуточных версий 10 участников) | |||
| Строка 1: | Строка 1: | ||
'''C3-линеаризация суперкласса''' ({{lang-en|C3 superclass linearization}}) — [[алгоритм]], используемый преимущественно для получения устойчивой линеаризации иерархии [[Множественное наследование|множественного наследования]] в [[Объектно-ориентированное программирование|объектно-ориентированном программировании]]. Данная линеаризация используется для определения порядка, в котором должны наследоваться методы, что часто в англоязычной литературе обозначается как «MRO» (сокращение от «Method Resolution Order», то есть «порядок разрешения метода»). C3 в названии указывает на три главные особенности итоговой линеаризации: устойчивый и расширяющийся (по старшинству) |
'''C3-линеаризация суперкласса''' ({{lang-en|C3 superclass linearization}}) — [[алгоритм]], используемый преимущественно для получения устойчивой линеаризации иерархии [[Множественное наследование|множественного наследования]] в [[Объектно-ориентированное программирование|объектно-ориентированном программировании]]. Данная линеаризация используется для определения порядка, в котором должны наследоваться методы, что часто в англоязычной литературе обозначается как «MRO» (сокращение от «Method Resolution Order», то есть «порядок разрешения метода»). C3 в названии указывает на три главные особенности итоговой линеаризации: устойчивый и расширяющийся (по старшинству) {{iw|Граф (тип данных)|граф|en|Graph (abstract data type)}}, сохранение локального порядка старшинства, а также монотонность. Данная теория впервые была представлена в [[1996 год]]у в рамках конференции [[OOPSLA]], в документе, озаглавленном «Монотонная линеаризация суперкласса для языка Dylan»<ref>{{cite conference |
||
| |
|date = 1996-06-28 |
||
| |
|title = A Monotonic Superclass Linearization for Dylan |
||
| |
|url = http://www.webcom.com/haahr/dylan/linearization-oopsla96.html |
||
| |
|book-title = [[OOPSLA]] '96 Conference Proceedings |
||
| |
|pages = 69–82 |
||
| |
|publisher = [[ACM Press]] |
||
| |
|doi = 10.1145/236337.236343 |
||
| |
|id = ISBN 0-89791-788-X |
||
|archiveurl = https://web.archive.org/web/20000817033012/http://www.webcom.com/haahr/dylan/linearization-oopsla96.html |
|||
}}</ref>. Впоследствии данный алгоритм был выбран как алгоритм по умолчанию для разрешения методов в языке программирования [[Python]] 2.3 (и последующих версиях), [[Perl 6]] и [[Виртуальная машина|виртуальной машине]] [[Parrot]]. Он также доступен в виде альтернативы (не являясь MRO по умолчанию) в ядре [[Perl|Perl 5]], начиная с версии 5.10.0. Расширенная реализация для более ранних версий Perl 5 носит название [http://search.cpan.org/dist/Class-C3 Class::C3] и существует в [[CPAN]]. |
|||
|archivedate = 2000-08-17 |
|||
|url-status = dead |
|||
|accessdate = 2009-12-14 |
|||
}} {{Cite web |url=http://www.webcom.com/haahr/dylan/linearization-oopsla96.html |title=Источник |access-date=2009-12-14 |archive-date=2000-08-17 |archive-url=https://web.archive.org/web/20000817033012/http://www.webcom.com/haahr/dylan/linearization-oopsla96.html |url-status=unfit }}</ref>. Впоследствии данный алгоритм был выбран как алгоритм по умолчанию для разрешения методов в языке программирования [[Python]] 2.3 (и последующих версиях), [[Perl 6]] и [[Виртуальная машина|виртуальной машине]] [[Parrot]]. Он также доступен в виде альтернативы (не являясь MRO по умолчанию) в ядре [[Perl|Perl 5]], начиная с версии 5.10.0. Расширенная реализация для более ранних версий Perl 5 носит название [http://search.cpan.org/dist/Class-C3 Class::C3] и существует в [[CPAN]]. |
|||
=== Пример === |
|||
Для |
|||
[[File:C3_linearization_example.svg|right|300px|thumb|Граф зависимостей данного примера.]] |
|||
class O |
|||
class A extends O |
|||
class B extends O |
|||
class C extends O |
|||
class D extends O |
|||
class E extends O |
|||
class K1 extends A, B, C |
|||
class K2 extends D, B, E |
|||
class K3 extends D, A |
|||
class Z extends K1, K2, K3 |
|||
Линеаризация Z считается как |
|||
L(O) := [O] // линеаризация O тривиально представляет собой единичный список [O], потому что O не имеет родителей |
|||
L(A) := [A] + merge(L(O), [O]) // линеаризация A - это A плюс объединение линеаризаций его родителей с списком родителей... |
|||
= [A] + merge([O], [O]) = [A, O] // ...что просто добавляет A в линеаризацию его единственного родителя |
|||
L(B) := [B, O] // линеаризации B, C, D и E вычисляются аналогично линеаризации A |
|||
L(C) := [C, O] |
|||
L(D) := [D, O] |
|||
L(E) := [E, O] |
|||
L(K1) := [K1] + merge(L(C), L(B), L(A), [C, A, B]) // сначала найдем линеаризации родителей K1: L(C), L(B) и L(A), и объединим их с списком родителей [C, A, B] |
|||
= [K1] + merge([C, O], [B, O], [A, O], [C, A, B]) // класс C - хороший кандидат для первого шага слияния, потому что он появляется только в начале первого и последнего списка |
|||
= [K1, C] + merge([O], [B, O], [A, O], [A, B]) // класс O - не является хорошим кандидатом для следующего шага слияния, потому что он также появляется в хвостах списка 2 и 3, класс B тоже не подходит; но класс A - хороший кандидат |
|||
= [K1, C, A] + merge([O], [B, O], [O], [B]) // класс B - хороший кандидат; класс O все еще появляется в хвосте списка 2 |
|||
= [K1, C, A, B] + merge([O], [O], [O]) // наконец, класс O - допустимый кандидат, что также завершает все оставшиеся списки |
|||
= [K1, C, A, B, O] |
|||
L(K3) := [K3] + merge(L(A), L(D), [A, D]) |
|||
= [K3] + merge([A, O], [D, O], [A, D]) // выбираем A |
|||
= [K3, A] + merge([O], [D, O], [D]) // отбрасываем O, выбираем D |
|||
= [K3, A, D] + merge([O], [O]) // выбираем O |
|||
= [K3, A, D, O] |
|||
L(K2) := [K2] + merge(L(B), L(D), L(E), [B, D, E]) |
|||
= [K2] + merge([B, O], [D, O], [E, O], [B, D, E]) // выбираем B |
|||
= [K2, B] + merge([O], [D, O], [E, O], [D, E]) // отбрасываем O, выбираем D |
|||
= [K2, B, D] + merge([O], [O], [E, O], [E]) // отбрасываем O, выбираем E |
|||
= [K2, B, D, E] + merge([O], [O], [O]) // выбираем O |
|||
= [K2, B, D, E, O] |
|||
L(Z) := [Z] + merge(L(K1), L(K3), L(K2), [K1, K3, K2]) |
|||
= [Z] + merge([K1, C, A, B, O], [K3, A, D, O], [K2, B, D, E, O], [K1, K3, K2]) // выбираем K1 |
|||
= [Z, K1] + merge([C, A, B, O], [K3, A, D, O], [K2, B, D, E, O], [K3, K2]) // выбираем C |
|||
= [Z, K1, C] + merge([A, B, O], [K3, A, D, O], [K2, B, D, E, O], [K3, K2]) // отбрасываем A, выбираем K3 |
|||
= [Z, K1, C, K3] + merge([A, B, O], [A, D, O], [K2, B, D, E, O], [K2]) // выбираем A |
|||
= [Z, K1, C, K3, A] + merge([B, O], [D, O], [K2, B, D, E, O], [K2]) // отбрасываем B, отбрасываем D, выбираем K2 |
|||
= [Z, K1, C, K3, A, K2] + merge([B, O], [D, O], [B, D, E, O]) // выбираем B |
|||
= [Z, K1, C, K3, A, K2, B] + merge([O], [D, O], [D, E, O]) // отбрасываем O, выбираем D |
|||
= [Z, K1, C, K3, A, K2, B, D] + merge([O], [O], [E, O]) // отбрасываем O, выбираем E |
|||
= [Z, K1, C, K3, A, K2, B, D, E] + merge([O], [O], [O]) // выбираем O |
|||
= [Z, K1, C, K3, A, K2, B, D, E, O] // готово |
|||
Обозначения: |
|||
L(Class) - линеаризация класса Class |
|||
[A,B,C] - список из трех элементов, где голова это A, а хвост [B,C] |
|||
merge - слияние списков |
|||
Функция merge осуществляет слияние списков таким образом, чтобы каждый элемент встречался в результате ровно один раз, этим она похожа на слияние множеств, но тут важен порядок следования элементов в списке. Функция merge работает следующим образом - она перебирает списки-аргументы по порядку упоминания (слева направо), выбирая первый элемент, который может быть первым в нескольких списках, но нигде не упоминается вторым и далее, и перемещает его в список-результат, исключая из списков-аргументов, повторяя эту процедуру несколько раз, пока все элементы не переместятся из списков-аргументов в список-результат. Если на каком-то этапе возникает ситуация, что нельзя выбрать элемент-кандидат, удовлетворяющий указанному условию, т.е. если во всех списках-аргументах первые элементы встречаются в других списках-аргументах не первыми, итоговый список не создаётся. |
|||
=== Пример Python3 === |
|||
Создадим отображение классов в виде их имен<syntaxhighlight lang="python3"> |
|||
class Type(type): |
|||
def __repr__(cls): |
|||
# Will make it so that repr(O) is "O" instead of "<__main__.O>", |
|||
# and the same for any subclasses of O. |
|||
return cls.__name__ |
|||
class O(object, metaclass=Type): pass |
|||
</syntaxhighlight>Определим базовые классы<syntaxhighlight lang="python3"> |
|||
class A(O): pass |
|||
class B(O): pass |
|||
class C(O): pass |
|||
class D(O): pass |
|||
class E(O): pass |
|||
</syntaxhighlight>Построим дерево наследования<syntaxhighlight lang="python3"> |
|||
class K1(C, A, B): pass |
|||
class K3(A, D): pass |
|||
class K2(B, D, E): pass |
|||
class Z(K1, K3, K2): pass |
|||
</syntaxhighlight>Проверяем mro<syntaxhighlight> |
|||
>>> Z.mro() |
|||
[Z, K1, C, K3, A, K2, B, D, E, O, <class 'object'>] |
|||
</syntaxhighlight> |
|||
=== Пример в Raku === |
|||
<syntaxhighlight lang="raku"> |
|||
class A {} |
|||
class B {} |
|||
class C {} |
|||
class D {} |
|||
class E {} |
|||
class K1 is C is A is B {} |
|||
class K3 is A is D {} |
|||
class K2 is B is D is E {} |
|||
class Z is K1 is K3 is K2 {} |
|||
say Z.^mro; # OUTPUT: ((Z) (K1) (C) (K3) (A) (K2) (B) (D) (E) (Any) (Mu)) |
|||
</syntaxhighlight> |
|||
== Примечания == |
== Примечания == |
||
| Строка 17: | Строка 128: | ||
== Ссылки == |
== Ссылки == |
||
* [http://www.python.org/download/releases/2.3/mro/ Использование C3 MRO в Python 2.3] {{ref-en}} |
* [http://www.python.org/download/releases/2.3/mro/ Использование C3 MRO в Python 2.3] {{ref-en}} |
||
* [http://use.perl.org/~autrijus/journal/25768 Perl 6 будет использовать C3 MRO] {{ref-en}} |
* [https://web.archive.org/web/20100327170727/http://use.perl.org/~autrijus/journal/25768 Perl 6 будет использовать C3 MRO] {{ref-en}} |
||
* [http://aspn.activestate.com/ASPN/Mail/Message/perl6-internals/2746631 Parrot использует C3 MRO] {{ref-en}} |
* [https://web.archive.org/web/20070208165958/http://aspn.activestate.com/ASPN/Mail/Message/perl6-internals/2746631 Parrot использует C3 MRO] {{ref-en}} |
||
* [http://search.cpan.org/dist/perl-5.10.0/lib/mro.pm C3 MRO доступна в Perl 5.10] {{ref-en}} |
* [http://search.cpan.org/dist/perl-5.10.0/lib/mro.pm C3 MRO доступна в Perl 5.10] {{ref-en}} |
||
* [http://search.cpan.org/dist/Class-C3/ Расширение Perl 5 для C3 MRO в CPAN] {{ref-en}} |
* [http://search.cpan.org/dist/Class-C3/ Расширение Perl 5 для C3 MRO в CPAN] {{ref-en}} |
||
{{Compu-prog-stub}} |
|||
[[Категория:Алгоритмы]] |
[[Категория:Алгоритмы]] |
||
[[Категория:Наследование (программирование)]] |
[[Категория:Наследование (программирование)]] |
||
[[en:C3 linearization]] |
|||
Текущая версия от 20:04, 14 сентября 2024
C3-линеаризация суперкласса (англ. C3 superclass linearization) — алгоритм, используемый преимущественно для получения устойчивой линеаризации иерархии множественного наследования в объектно-ориентированном программировании. Данная линеаризация используется для определения порядка, в котором должны наследоваться методы, что часто в англоязычной литературе обозначается как «MRO» (сокращение от «Method Resolution Order», то есть «порядок разрешения метода»). C3 в названии указывает на три главные особенности итоговой линеаризации: устойчивый и расширяющийся (по старшинству) граф[англ.]*, сохранение локального порядка старшинства, а также монотонность. Данная теория впервые была представлена в 1996 году в рамках конференции OOPSLA, в документе, озаглавленном «Монотонная линеаризация суперкласса для языка Dylan»[1]. Впоследствии данный алгоритм был выбран как алгоритм по умолчанию для разрешения методов в языке программирования Python 2.3 (и последующих версиях), Perl 6 и виртуальной машине Parrot. Он также доступен в виде альтернативы (не являясь MRO по умолчанию) в ядре Perl 5, начиная с версии 5.10.0. Расширенная реализация для более ранних версий Perl 5 носит название Class::C3 и существует в CPAN.
Пример
[править | править код]Для
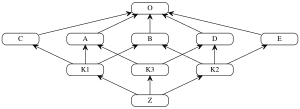
class O class A extends O class B extends O class C extends O class D extends O class E extends O class K1 extends A, B, C class K2 extends D, B, E class K3 extends D, A class Z extends K1, K2, K3
Линеаризация Z считается как
L(O) := [O] // линеаризация O тривиально представляет собой единичный список [O], потому что O не имеет родителей L(A) := [A] + merge(L(O), [O]) // линеаризация A - это A плюс объединение линеаризаций его родителей с списком родителей... = [A] + merge([O], [O]) = [A, O] // ...что просто добавляет A в линеаризацию его единственного родителя L(B) := [B, O] // линеаризации B, C, D и E вычисляются аналогично линеаризации A L(C) := [C, O] L(D) := [D, O] L(E) := [E, O] L(K1) := [K1] + merge(L(C), L(B), L(A), [C, A, B]) // сначала найдем линеаризации родителей K1: L(C), L(B) и L(A), и объединим их с списком родителей [C, A, B] = [K1] + merge([C, O], [B, O], [A, O], [C, A, B]) // класс C - хороший кандидат для первого шага слияния, потому что он появляется только в начале первого и последнего списка = [K1, C] + merge([O], [B, O], [A, O], [A, B]) // класс O - не является хорошим кандидатом для следующего шага слияния, потому что он также появляется в хвостах списка 2 и 3, класс B тоже не подходит; но класс A - хороший кандидат = [K1, C, A] + merge([O], [B, O], [O], [B]) // класс B - хороший кандидат; класс O все еще появляется в хвосте списка 2 = [K1, C, A, B] + merge([O], [O], [O]) // наконец, класс O - допустимый кандидат, что также завершает все оставшиеся списки = [K1, C, A, B, O] L(K3) := [K3] + merge(L(A), L(D), [A, D]) = [K3] + merge([A, O], [D, O], [A, D]) // выбираем A = [K3, A] + merge([O], [D, O], [D]) // отбрасываем O, выбираем D = [K3, A, D] + merge([O], [O]) // выбираем O = [K3, A, D, O] L(K2) := [K2] + merge(L(B), L(D), L(E), [B, D, E]) = [K2] + merge([B, O], [D, O], [E, O], [B, D, E]) // выбираем B = [K2, B] + merge([O], [D, O], [E, O], [D, E]) // отбрасываем O, выбираем D = [K2, B, D] + merge([O], [O], [E, O], [E]) // отбрасываем O, выбираем E = [K2, B, D, E] + merge([O], [O], [O]) // выбираем O = [K2, B, D, E, O] L(Z) := [Z] + merge(L(K1), L(K3), L(K2), [K1, K3, K2]) = [Z] + merge([K1, C, A, B, O], [K3, A, D, O], [K2, B, D, E, O], [K1, K3, K2]) // выбираем K1 = [Z, K1] + merge([C, A, B, O], [K3, A, D, O], [K2, B, D, E, O], [K3, K2]) // выбираем C = [Z, K1, C] + merge([A, B, O], [K3, A, D, O], [K2, B, D, E, O], [K3, K2]) // отбрасываем A, выбираем K3 = [Z, K1, C, K3] + merge([A, B, O], [A, D, O], [K2, B, D, E, O], [K2]) // выбираем A = [Z, K1, C, K3, A] + merge([B, O], [D, O], [K2, B, D, E, O], [K2]) // отбрасываем B, отбрасываем D, выбираем K2 = [Z, K1, C, K3, A, K2] + merge([B, O], [D, O], [B, D, E, O]) // выбираем B = [Z, K1, C, K3, A, K2, B] + merge([O], [D, O], [D, E, O]) // отбрасываем O, выбираем D = [Z, K1, C, K3, A, K2, B, D] + merge([O], [O], [E, O]) // отбрасываем O, выбираем E = [Z, K1, C, K3, A, K2, B, D, E] + merge([O], [O], [O]) // выбираем O = [Z, K1, C, K3, A, K2, B, D, E, O] // готово
Обозначения:
L(Class) - линеаризация класса Class [A,B,C] - список из трех элементов, где голова это A, а хвост [B,C] merge - слияние списков
Функция merge осуществляет слияние списков таким образом, чтобы каждый элемент встречался в результате ровно один раз, этим она похожа на слияние множеств, но тут важен порядок следования элементов в списке. Функция merge работает следующим образом - она перебирает списки-аргументы по порядку упоминания (слева направо), выбирая первый элемент, который может быть первым в нескольких списках, но нигде не упоминается вторым и далее, и перемещает его в список-результат, исключая из списков-аргументов, повторяя эту процедуру несколько раз, пока все элементы не переместятся из списков-аргументов в список-результат. Если на каком-то этапе возникает ситуация, что нельзя выбрать элемент-кандидат, удовлетворяющий указанному условию, т.е. если во всех списках-аргументах первые элементы встречаются в других списках-аргументах не первыми, итоговый список не создаётся.
Пример Python3
[править | править код]Создадим отображение классов в виде их имен
class Type(type):
def __repr__(cls):
# Will make it so that repr(O) is "O" instead of "<__main__.O>",
# and the same for any subclasses of O.
return cls.__name__
class O(object, metaclass=Type): pass
Определим базовые классы
class A(O): pass
class B(O): pass
class C(O): pass
class D(O): pass
class E(O): pass
Построим дерево наследования
class K1(C, A, B): pass
class K3(A, D): pass
class K2(B, D, E): pass
class Z(K1, K3, K2): pass
Проверяем mro
>>> Z.mro()
[Z, K1, C, K3, A, K2, B, D, E, O, <class 'object'>]Пример в Raku
[править | править код]class A {}
class B {}
class C {}
class D {}
class E {}
class K1 is C is A is B {}
class K3 is A is D {}
class K2 is B is D is E {}
class Z is K1 is K3 is K2 {}
say Z.^mro; # OUTPUT: ((Z) (K1) (C) (K3) (A) (K2) (B) (D) (E) (Any) (Mu))
Примечания
[править | править код]- ↑ "A Monotonic Superclass Linearization for Dylan". OOPSLA '96 Conference Proceedings. ACM Press. 28 июня 1996. pp. 69–82. doi:10.1145/236337.236343. ISBN 0-89791-788-X. Архивировано из оригинала 17 августа 2000. Дата обращения: 14 декабря 2009.
{{cite conference}}:|archive-date=/|archive-url=несоответствие временной метки; предлагается 17 августа 2000 (справка) Источник. Дата обращения: 14 декабря 2009. Архивировано 17 августа 2000 года.
Ссылки
[править | править код]- Использование C3 MRO в Python 2.3 (англ.)
- Perl 6 будет использовать C3 MRO (англ.)
- Parrot использует C3 MRO (англ.)
- C3 MRO доступна в Perl 5.10 (англ.)
- Расширение Perl 5 для C3 MRO в CPAN (англ.)