Двумерное пространство: различия между версиями
| [отпатрулированная версия] | [отпатрулированная версия] |
отмена правки 97563885 участника 82.208.127.242 (обс.), было правильно Метка: отмена |
отклонено последнее 1 изменение от AVALSAWALS12345678901 Метка: ручная отмена |
||
| (не показано 14 промежуточных версий 12 участников) | |||
| Строка 1: | Строка 1: | ||
{{Другие значения|2D}} |
{{Другие значения|2D}} |
||
{{Другие значения|Пространство}} |
{{Другие значения|Пространство}} |
||
'''Двуме́рное простра́нство''' (иногда говорят '''двухме́рное пространство''') — [[Геометрия|геометрическая]] [[модель]] плоской проекции физического мира |
'''Двуме́рное простра́нство''' (иногда говорят '''двухме́рное пространство''') — [[Геометрия|геометрическая]] [[модель]] плоской проекции физического мира. Двумерным пространством считается <math>n</math>-[[Размерность пространства|мерное]] [[Пространство (математика)|пространство]], где <math>n=2</math>. |
||
Примером двумерного пространства является [[Плоскость (геометрия)|плоскость]] (двумерное евклидово пространство). Точки данного пространства возможно задать всего двумя числами |
Примером двумерного пространства является [[Плоскость (геометрия)|плоскость]] (двумерное евклидово пространство). Точки данного пространства возможно задать всего двумя числами: <math>x, y</math>, называемыми на евклидовой плоскости [[Абсцисса|абсциссой]] и [[Ордината|ординатой]]. Плоские объекты характеризуются не только длиной, но и шириной<ref name=Gush>{{Cite web |url=http://fmclass.ru/math.php?id=49a0390719b7b |title=Гущин Д. Д. Пространство как математическое понятие |access-date=2012-02-11 |archive-date=2016-03-04 |archive-url=https://web.archive.org/web/20160304073828/http://fmclass.ru/math.php?id=49a0390719b7b |deadlink=no }}</ref>, в отличие от [[Одномерное пространство|одномерных]]. |
||
Другие поверхности трёхмерного евклидова пространства могут быть рассмотрены как двумерные неевклидовы пространства. |
Другие поверхности трёхмерного евклидова пространства, кроме плоскости, могут быть рассмотрены как двумерные неевклидовы пространства. |
||
== Геометрия двумерного пространства == |
== Геометрия двумерного пространства == |
||
| Строка 14: | Строка 14: | ||
==== [[Выпуклый многоугольник|Выпуклые]] ==== |
==== [[Выпуклый многоугольник|Выпуклые]] ==== |
||
Символ {p} ([[символ Шлефли]]) обозначает [[Правильный многоугольник|правильный |
Символ <math>{p}</math> ([[символ Шлефли]]) обозначает [[Правильный многоугольник|правильный <math>p</math>-угольник]]. |
||
{| class="wikitable" style="text-align:center;" |
{| class="wikitable" style="text-align:center;" |
||
|- bgcolor="#e0e0e0" valign="top" |
|- bgcolor="#e0e0e0" valign="top" |
||
!Название |
!Название |
||
![[Правильный треугольник| |
![[Правильный треугольник|треугольник]]<br />([[Симплекс|2-симплекс]]) |
||
![[ |
![[квадрат]]<br />([[Гиперкуб|2-куб]] и [[Гипероктаэдр|2-октаэдр]]) |
||
![[Правильный пятиугольник| |
![[Правильный пятиугольник|пятиугольник]]<br />([[Пятиугольный многогранник|2-додекаэдр и 2-икосаэдр]]) |
||
![[Правильный шестиугольник| |
![[Правильный шестиугольник|шестиугольник]] |
||
![[Правильный семиугольник| |
![[Правильный семиугольник|семиугольник]] |
||
![[Правильный восьмиугольник| |
![[Правильный восьмиугольник|восьмиугольник]] |
||
|- bgcolor="#ffe0e0" |
|- bgcolor="#ffe0e0" |
||
![[Символ Шлефли]] |
![[Символ Шлефли]] |
||
|{3} |
|<math>\{3\}</math> |
||
|{4} |
|<math>\{4\}</math> |
||
|{5} |
|<math>\{5\}</math> |
||
|{6} |
|<math>\{6\}</math> |
||
|{7} |
|<math>\{7\}</math> |
||
|{8} |
|<math>\{8\}</math> |
||
|- |
|- |
||
!Вид |
!Вид |
||
| Строка 43: | Строка 43: | ||
|- |
|- |
||
!Название |
!Название |
||
![[Правильный девятиугольник| |
![[Правильный девятиугольник|девятиугольник]] |
||
![[десятиугольник]] |
|||
![[Десятиугольник]] |
|||
![[одиннадцатиугольник]] |
|||
![[Одиннадцатиугольник]] |
|||
![[двенадцатиугольник|двенадцати-<br />угольник]] |
|||
![[Двенадцатиугольник]] |
|||
! |
![[Тринадцатиугольник|тринадцати-<br />угольник]] |
||
![[Четырнадцатиугольник]] |
![[Четырнадцатиугольник|четырнадцати-<br />угольник]] |
||
|- bgcolor="#ffe0e0" |
|- bgcolor="#ffe0e0" |
||
![[Символ Шлефли]] |
![[Символ Шлефли]] |
||
|{9} |
|<math>\{9\}</math> |
||
|{10} |
|<math>\{10\}</math> |
||
|{11} |
|<math>\{11\}</math> |
||
|{12} |
|<math>\{12\}</math> |
||
|{13} |
|<math>\{13\}</math> |
||
|{14} |
|<math>\{14\}</math> |
||
|- |
|- |
||
!Вид |
!Вид |
||
| Строка 67: | Строка 67: | ||
|- |
|- |
||
!Название |
!Название |
||
! |
![[Пятнадцатиугольник|пятнадцати-<br />угольник]] |
||
! |
![[Шестнадцатиугольник|шестнадцати-<br />угольник]] |
||
![[Правильный семнадцатиугольник| |
![[Правильный семнадцатиугольник|семнадцатиугольник]] |
||
![[Восемнадцатиугольник]] |
![[Восемнадцатиугольник|восемнадцати-<br />угольник]] |
||
! |
![[Девятнадцатиугольник|девятнадцати-<br />угольник]] |
||
![[двадцатиугольник]] |
|||
!{{iw|Двадцатиугольник||en|Icosagon}} |
|||
| |
|'''{{nobr|[[Правильный многоугольник|n-угольник]]}}''' |
||
|- bgcolor="#ffe0e0" |
|- bgcolor="#ffe0e0" |
||
![[Символ Шлефли]] |
![[Символ Шлефли]] |
||
|{15} |
|<math>\{15\}</math> |
||
|{16} |
|<math>\{16\}</math> |
||
|{17} |
|<math>\{17\}</math> |
||
|{18} |
|<math>\{18\}</math> |
||
|{19} |
|<math>\{19\}</math> |
||
|{20} |
|<math>\{20\}</math> |
||
|<math>\{n\}</math> |
|||
|{''n''} |
|||
|- |
|- |
||
!Вид |
!Вид |
||
Текущая версия от 04:47, 15 сентября 2024
Двуме́рное простра́нство (иногда говорят двухме́рное пространство) — геометрическая модель плоской проекции физического мира. Двумерным пространством считается -мерное пространство, где .
Примером двумерного пространства является плоскость (двумерное евклидово пространство). Точки данного пространства возможно задать всего двумя числами: , называемыми на евклидовой плоскости абсциссой и ординатой. Плоские объекты характеризуются не только длиной, но и шириной[1], в отличие от одномерных.
Другие поверхности трёхмерного евклидова пространства, кроме плоскости, могут быть рассмотрены как двумерные неевклидовы пространства.
Геометрия двумерного пространства
[править | править код]Многогранники
[править | править код]В двумерном пространстве существует бесконечно много правильных многогранников: правильные многоугольники. Примеры последних приведены ниже:
Символ (символ Шлефли) обозначает правильный -угольник.
Гиперсфера
[править | править код]Гиперсферой в двумерном пространстве является окружность, которую иногда называют 1-сфера, потому что её поверхность является одномерной. Площадь части плоскости, заключённой внутри гиперсферы (площадь круга) равна:
- ,
где — радиус окружности.
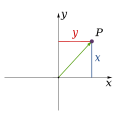
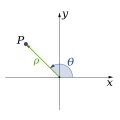
Системы координат в двумерном пространстве
[править | править код]Наиболее распространённые координатные системы в двумерном евклидовом пространстве — прямоугольная (декартова) система координат и полярная система координат. На 2-сфере используется географическая координатная система.
См. также
[править | править код]Примечания
[править | править код]- ↑ Гущин Д. Д. Пространство как математическое понятие. Дата обращения: 11 февраля 2012. Архивировано 4 марта 2016 года.