Граф Титце: различия между версиями

Материал из Википедии — свободной энциклопедии
Перейти к навигации Перейти к поиску
Интерактивная навигация по истории
(Показать все непатрулированные изменения)
[отпатрулированная версия][непроверенная версия]
← Предыдущая правка
Содержимое удалено Содержимое добавлено
ВизуальныйВики-текст
Нет описания правки
 
(не показано 13 промежуточных версий 9 участников)
Строка 3: Строка 3:
| Название = Граф Титце
| Название = Граф Титце
| Изображение = Tietze's graph.svg
| Изображение = Tietze's graph.svg
| namesake = {{не переведено 5|Титце, Генрих Франц Фридрих|Генрих Франц Фридрих Титце||Heinrich Franz Friedrich Tietze}}
| namesake = [[Титце, Генрих Фридрих|Генрих Титце]]
| Вершин = 12
| Вершин = 12
| Рёбер = 18
| Рёбер = 18
Строка 15: Строка 15:
}}
}}


В [[Теория графов|теории графов]] '''граф Титце''' – это [[Неориентированный граф|неориентированный]] [[кубический граф]] с 12 вершинами и 18 рёбрами.
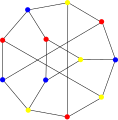
В [[Теория графов|теории графов]] '''граф Титце''' — это [[Неориентированный граф|неориентированный]] [[кубический граф]] с 12 вершинами и 18 рёбрами.
Граф назван именем {{не переведено 5|Титце, Генрих Франц Фридрих|Генриха Франца Фридриха Титце||Heinrich Franz Friedrich Tietze}}, показавшего в 1910, что [[Лента Мёбиуса|ленту Мёбиуса]] можно разделить на шесть областей, касающихся друг друга – три вдоль границы ленты и три вдоль центральной линии – а потому для графов, допускающих {{не переведено 5|Вложение графа|вложение||graph embedding}} в ленту Мёбиуса, может потребоваться [[Раскраска графов|шесть цветов]] {{sfn|Tietze|1910|с=155-159}}. Граничные сегменты областей Титца разделения ленты Мёбиуса (включая сегменты вдоль границы самой ленты) образуют вложение графа Титце.
Граф назван именем [[Титце, Генрих Фридрих|Генриха Титце]], показавшего в 1910 году, что [[Лента Мёбиуса|ленту Мёбиуса]] можно разделить на шесть областей, касающихся друг друга — три вдоль границы ленты и три вдоль центральной линии — а потому для графов, допускающих [[Вложение графа|вложение]] в ленту Мёбиуса, может потребоваться [[Раскраска графов|шесть цветов]]{{sfn|Tietze|1910|с=155-159}}. Граничные сегменты областей Титца разделения ленты Мёбиуса (включая сегменты вдоль границы самой ленты) образуют вложение графа Титце.


==Связь с графом Петерсена ==
== Связь с графом Петерсена ==
Граф Титце можно получить из [[Граф Петерсена|графа Петерсена]] заменой одной из его вершин [[треугольник]]ом{{sfn|Clark, Entringer|1983|с=57–68 }}.
Граф Титце можно получить из [[Граф Петерсена|графа Петерсена]] заменой одной из его вершин [[треугольник]]ом{{sfn|Clark, Entringer|1983|с=57–68 }}.
Подобно графу Титце граф Петерсена служит границами шести взаимно соприкасающихся шести областей, но в [[Проективная плоскость|проективной плоскости]], а не на ленте Мёбиуса. Если вырезать окрестность некоторой вершины этого разбиения проективной плоскости, вершина заменяется границами этой дыры, что даёт в точности построение графа Титце, описанное выше.
Подобно графу Титце граф Петерсена служит границами шести взаимно соприкасающихся областей, но в [[Проективная плоскость|проективной плоскости]], а не на ленте Мёбиуса. Если вырезать окрестность некоторой вершины этого разбиения проективной плоскости, вершина заменяется границами этой дыры, что даёт в точности построение графа Титце, описанное выше.


==Гамильтоновость==
== Гамильтоновость ==
И граф Титце, и граф Петерсона ''максимально негамильтоновы'' – они не имеют [[Гамильтонов граф|гамильтонова цикла]], но любые две несмежные вершины могут быть соединены гамильтоновым путём {{sfn|Clark, Entringer|1983|с=57–68 }}. Граф Титце и граф Петерсена являются единственными [[Вершинно k-связный граф|вершинно 2-связными]] кубическими негамильтоновыми графами с 12 или менее вершинами {{sfn|Punnim, Saenpholphat, Thaithae|2007|с=83–86}}.
И граф Титце, и граф Петерсона ''максимально негамильтоновы'' — они не имеют [[Гамильтонов граф|гамильтонова цикла]], но любые две несмежные вершины могут быть соединены гамильтоновым путём{{sfn|Clark, Entringer|1983|с=57–68 }}. Граф Титце и граф Петерсена являются единственными [[Вершинно k-связный граф|вершинно 2-связными]] кубическими негамильтоновыми графами с 12 или менее вершинами{{sfn|Punnim, Saenpholphat, Thaithae|2007|с=83–86}}.


В отличие от графа Петерсена, граф Титце не является {{не переведено 5|Гипогамильтоновый граф|гипогамильтоновым||hypohamiltonian graph}} – удаление одной из трёх вершин треугольника образует меньший граф, остающийся негамильтоновым.
В отличие от графа Петерсена, граф Титце не является [[Гипогамильтоновый граф|гипогамильтоновым]] — удаление одной из трёх вершин треугольника образует меньший граф, остающийся негамильтоновым.


==Рёберная раскраска и совершенные паросочетания ==
== Рёберная раскраска и совершенные паросочетания ==
[[Рёберная раскраска]] графа Титце требует четыре цвета. То есть его хроматический индекс равен 4. Это эквивалентно тому, что рёбра графа Титца могут быть разделены на четыре [[Паросочетание|паросочетания]], но не меньше.
[[Рёберная раскраска]] графа Титце требует четырёх цветов, то есть его хроматический индекс равен 4. Это эквивалентно тому, что рёбра графа Титца могут быть разделены на четыре [[Паросочетание|паросочетания]], но не меньше.


Граф Титце удовлетворяет части требований определения [[Снарк (теория графов)|снарка]] – он является кубическим графом [[Мост (теория графов)|без мостов]] и его рёбра не могут быть выкрашены в 3 цвета. Однако некоторые авторы ограничивают снарки графами без 3-циклов и 4-циклов, а при этих более сильных условиях граф Титце не является снарком. Граф Титце изоморфен графу J<sub>3</sub>, графу из бесконечного семейства [[Снарк «Цветок»|снарков «Цветок»]], предложенных Р. Исаакксом в 1975 {{sfn|Isaacs|1975|с=221–239}}.
Граф Титце удовлетворяет части требований определения [[Снарк (теория графов)|снарка]] — он является кубическим графом [[Мост (теория графов)|без мостов]] и его рёбра не могут быть выкрашены в 3 цвета. Однако некоторые авторы ограничивают снарки графами без 3-циклов и 4-циклов, а при этих более сильных условиях граф Титце не является снарком. Граф Титце изоморфен графу J<sub>3</sub>, графу из бесконечного семейства [[Снарк «Цветок»|снарков «Цветок»]], предложенных Р. Исаакксом в 1975 году{{sfn|Isaacs|1975|с=221–239}}.


В отличие от графа Петерсена, граф Титце может быть покрыт четырьмя [[Паросочетание|совершенными паросочетаниями]]. Это свойство играет ключевую роль в доказательстве, что проверка, можно ли покрыть граф четырьмя паросочетаниями, является [[NP-полная задача|NP-полной задачей]] {{sfn|Esperet, Mazzuoccolo|2014|с= 144–157}}.
В отличие от графа Петерсена, граф Титце может быть покрыт четырьмя [[Паросочетание|совершенными паросочетаниями]]. Это свойство играет ключевую роль в доказательстве, что проверка, можно ли покрыть граф четырьмя совершенными паросочетаниями, является [[NP-полная задача|NP-полной задачей]]{{sfn|Esperet, Mazzuoccolo|2014|с= 144–157}}.


==Дополнительные свойства==
== Дополнительные свойства ==
Граф Титце имеет хроматическое число 3, хроматический индекс 4, обхват 3 и диаметр 3. Его [[Задача о независимом множестве|число независимости]] равно 5, а [[Автоморфизм|группа автоморфизмов]] имеет порядок 12 и она изоморфна [[Диэдрическая группа|диэдрической группе]] D<sub>6</sub>, группе симметрий [[Шестиугольник|шестиугольника]], включающей как вращения, так и отражения. Эта группа содержит две орбиты размера 3 и одну размера 6 на вершинах, а потому этот граф не [[Вершинно-транзитивный граф|вершинно транзитивен]].
Граф Титце имеет хроматическое число 3, хроматический индекс 4, обхват 3 и диаметр 3. Его [[Задача о независимом множестве|число независимости]] равно 5, а [[Автоморфизм|группа автоморфизмов]] имеет порядок 12 и она изоморфна [[Диэдрическая группа|диэдрической группе]] D<sub>6</sub>, группе симметрий [[Шестиугольник|шестиугольника]], включающей как вращения, так и отражения. Эта группа содержит две орбиты размера 3 и одну размера 6 на вершинах, а потому этот граф не [[Вершинно-транзитивный граф|вершинно транзитивен]].


==Галерея==
== Галерея ==
<gallery>
<gallery>
File:Tietze's graph 3COL.svg| [[Раскраска графов|Хроматическое число]] графа Титце равно 3.
File:Tietze's graph 3COL.svg| [[Раскраска графов|Хроматическое число]] графа Титце равно 3.
File:Tietze's graph 4color edge.svg|[[Рёберная раскраска|Хроматический индекс]] графа Титца равен 4.
File:Tietze's graph 4color edge.svg|[[Рёберная раскраска|Хроматический индекс]] графа Титца равен 4.
File:Tietze-2crossings.svg|Граф Титце имеет [[Число пересечений (теория графов)|число пересечений]] 2 и он {{не переведено 5|1-планарный граф|1-планарен||1-planar graph}}.
File:Tietze-2crossings.svg|Граф Титце имеет [[Число пересечений (теория графов)|число пересечений]] 2 и он [[1-планарный граф|1-планарен]].
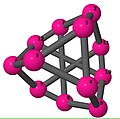
File:Y12W129EE4170908.jpg|Трёхмерное вложение графа Титце.
File:Y12W129EE4170908.jpg|Трёхмерное вложение графа Титце.
</gallery>
</gallery>


==См. также==
== См. также ==
*[[Граф Дюрера]] и {{не переведено 5|граф Франклина|||Franklin graph}}, два других кубических графа с 12 вершинами.
* [[Граф Дюрера]] и [[граф Франклина]], два других кубических графа с 12 вершинами.


==Примечания==
== Примечания ==
{{примечания|2}}
{{примечания|2}}

==Литература==
== Литература ==
*{{статья
* {{статья
⚫
|автор=L. Clark, R. Entringer
|ref=Clark, Entringer
|автор = L. Clark, R. Entringer
|ref = Clark, Entringer
|заглавие=Smallest maximally nonhamiltonian graphs
|заглавие = Smallest maximally nonhamiltonian graphs
|издание=Periodica Mathematica Hungarica
|издание = Periodica Mathematica Hungarica
|том=14
|том = 14
|выпуск=1
|выпуск = 1
|год=1983
|год = 1983
|doi=10.1007/BF02023582
|doi = 10.1007/BF02023582
}}
}}
*{{статья
* {{статья
|автор=Narong Punnim, Varaporn Saenpholphat, Sermsri Thaithae
|автор = Narong Punnim, Varaporn Saenpholphat, Sermsri Thaithae
|ref=Punnim, Saenpholphat, Thaithae
|ref = Punnim, Saenpholphat, Thaithae
| заглавие =Almost Hamiltonian cubic graphs
|заглавие = Almost Hamiltonian cubic graphs
| издание =International Journal of Computer Science and Network Security
|издание = International Journal of Computer Science and Network Security
|том=7
|том = 7
| выпуск =1
|выпуск = 1
| год =2007
|год = 2007
|url=http://paper.ijcsns.org/07_book/200701/200701A12.pdf
|url = http://paper.ijcsns.org/07_book/200701/200701A12.pdf
}}
}}
*{{статья
* {{статья
|автор=R. Isaacs
|автор = R. Isaacs
|ref=Isaacs
|ref = Isaacs
| заглавие =Infinite families of nontrivial trivalent graphs which are not Tait colorable
|заглавие = Infinite families of nontrivial trivalent graphs which are not Tait colorable
| издание =Amer. Math. Monthly
|издание = Amer. Math. Monthly
| том =82
|том = 82
| год =1975
|год = 1975
|doi=10.2307/2319844
|doi = 10.2307/2319844
|jstor=2319844
|jstor = 2319844
|выпуск=3
|выпуск = 3
|издательствоr=Mathematical Association of America
|издательство = Mathematical Association of America
}}
}}
*{{статья
* {{статья
|автор=Heinrich Tietze
|автор = Heinrich Tietze
|ref = Tietze
|ref=Tietze
|url=http://gdz.sub.uni-goettingen.de/no_cache/dms/load/img/?IDDOC=244202
|url = http://gdz.sub.uni-goettingen.de/no_cache/dms/load/img/?IDDOC=244202
| заглавие =Einige Bemerkungen zum Problem des Kartenfärbens auf einseitigen Flächen (Some remarks on the problem of map coloring on one-sided surfaces)
|заглавие = Einige Bemerkungen zum Problem des Kartenfärbens auf einseitigen Flächen (Some remarks on the problem of map coloring on one-sided surfaces)
| издание = [[German Mathematical Society|DMV]] Annual Report
|издание = [[German Mathematical Society|DMV]] Annual Report
| том =19
|том = 19
| год = 1910
|год = 1910
}}{{Недоступная ссылка|date=Июнь 2018 |bot=InternetArchiveBot }}
⚫
* {{статья
⚫
|автор = L. Clark, R. Entringer
|ref = Clark, Entringer
⚫
|заглавие = Smallest maximally nonhamiltonian graphs
⚫
|издание = Periodica Mathematica Hungarica
⚫
|том = 14
⚫
|выпуск = 1
⚫
|год = 1983
⚫
|doi = 10.1007/BF02023582
}}
}}
*{{статья
* {{статья
|автор=L. Clark, R. Entringer
|автор = L. Esperet, G. Mazzuoccolo
|ref= Clark, Entringer
|ref = Esperet, Mazzuoccolo
⚫
|arxiv = 1301.6926
⚫
| заглавие =Smallest maximally nonhamiltonian graphs
⚫
|выпуск = 2
⚫
| издание =Periodica Mathematica Hungarica
⚫
|издание = Journal of Graph Theory
⚫
| том =14
⚫
|mr = 3246172
⚫
| выпуск =1
⚫
|doi = 10.1002/jgt.21778
⚫
| год =1983
⚫
|заглавие = On cubic bridgeless graphs whose edge-set cannot be covered by four perfect matchings
⚫
|doi=10.1007/BF02023582
⚫
|том = 77
⚫
|год = 2014
}}
}}

⚫
*{{статья
[[Категория:Графы, имеющие собственные названия]]
|автор = L. Esperet, G. Mazzuoccolo
⚫
[[Категория:Регулярные графы]]
|ref= Esperet, Mazzuoccolo
⚫
| arxiv = 1301.6926
⚫
| выпуск = 2
⚫
| издание = Journal of Graph Theory
⚫
| mr = 3246172
⚫
| doi = 10.1002/jgt.21778
⚫
| заглавие = On cubic bridgeless graphs whose edge-set cannot be covered by four perfect matchings
⚫
| том = 77
⚫
| год = 2014
}}.
[[Категория:Индивидуальные графы]]
⚫
[[Категория:Регулярные графы]]
{{rq|checktranslate|style|grammar}}

Текущая версия от 11:54, 13 ноября 2024

Разбиение ленты Мёбиуса на шесть взаимно соприкасающихся областей. Вершины и рёбра разбиения образуют вложение графа Титце в ленту.
Граф Титце
Назван в честь Генрих Титце
Вершин 12
Рёбер 18
Радиус 3
Диаметр 3
Обхват 3
Автоморфизмы 12 (D6)
Хроматическое число 3
Хроматический индекс 4
Свойства Кубический
Снарк
Логотип Викисклада Медиафайлы на Викискладе

В теории графов граф Титце — это неориентированный кубический граф с 12 вершинами и 18 рёбрами. Граф назван именем Генриха Титце, показавшего в 1910 году, что ленту Мёбиуса можно разделить на шесть областей, касающихся друг друга — три вдоль границы ленты и три вдоль центральной линии — а потому для графов, допускающих вложение в ленту Мёбиуса, может потребоваться шесть цветов[1]. Граничные сегменты областей Титца разделения ленты Мёбиуса (включая сегменты вдоль границы самой ленты) образуют вложение графа Титце.

Связь с графом Петерсена

[править | править код]

Граф Титце можно получить из графа Петерсена заменой одной из его вершин треугольником[2]. Подобно графу Титце граф Петерсена служит границами шести взаимно соприкасающихся областей, но в проективной плоскости, а не на ленте Мёбиуса. Если вырезать окрестность некоторой вершины этого разбиения проективной плоскости, вершина заменяется границами этой дыры, что даёт в точности построение графа Титце, описанное выше.

Гамильтоновость

[править | править код]

И граф Титце, и граф Петерсона максимально негамильтоновы — они не имеют гамильтонова цикла, но любые две несмежные вершины могут быть соединены гамильтоновым путём[2]. Граф Титце и граф Петерсена являются единственными вершинно 2-связными кубическими негамильтоновыми графами с 12 или менее вершинами[3].

В отличие от графа Петерсена, граф Титце не является гипогамильтоновым — удаление одной из трёх вершин треугольника образует меньший граф, остающийся негамильтоновым.

Рёберная раскраска и совершенные паросочетания

[править | править код]

Рёберная раскраска графа Титце требует четырёх цветов, то есть его хроматический индекс равен 4. Это эквивалентно тому, что рёбра графа Титца могут быть разделены на четыре паросочетания, но не меньше.

Граф Титце удовлетворяет части требований определения снарка — он является кубическим графом без мостов и его рёбра не могут быть выкрашены в 3 цвета. Однако некоторые авторы ограничивают снарки графами без 3-циклов и 4-циклов, а при этих более сильных условиях граф Титце не является снарком. Граф Титце изоморфен графу J3, графу из бесконечного семейства снарков «Цветок», предложенных Р. Исаакксом в 1975 году[4].

В отличие от графа Петерсена, граф Титце может быть покрыт четырьмя совершенными паросочетаниями. Это свойство играет ключевую роль в доказательстве, что проверка, можно ли покрыть граф четырьмя совершенными паросочетаниями, является NP-полной задачей[5].

Дополнительные свойства

[править | править код]

Граф Титце имеет хроматическое число 3, хроматический индекс 4, обхват 3 и диаметр 3. Его число независимости равно 5, а группа автоморфизмов имеет порядок 12 и она изоморфна диэдрической группе D6, группе симметрий шестиугольника, включающей как вращения, так и отражения. Эта группа содержит две орбиты размера 3 и одну размера 6 на вершинах, а потому этот граф не вершинно транзитивен.

Галерея

[править | править код]

См. также

[править | править код]

Примечания

[править | править код]
  1. ↑ Tietze, 1910, с. 155-159.
  2. ↑ 1 2 Clark, Entringer, 1983, с. 57–68.
  3. ↑ Punnim, Saenpholphat, Thaithae, 2007, с. 83–86.
  4. ↑ Isaacs, 1975, с. 221–239.
  5. ↑ Esperet, Mazzuoccolo, 2014, с. 144–157.

Литература

[править | править код]
  • L. Clark, R. Entringer. Smallest maximally nonhamiltonian graphs // Periodica Mathematica Hungarica. — 1983. — Т. 14, вып. 1. — doi:10.1007/BF02023582.
  • Narong Punnim, Varaporn Saenpholphat, Sermsri Thaithae. Almost Hamiltonian cubic graphs // International Journal of Computer Science and Network Security. — 2007. — Т. 7, вып. 1.
  • R. Isaacs. Infinite families of nontrivial trivalent graphs which are not Tait colorable // Amer. Math. Monthly. — Mathematical Association of America, 1975. — Т. 82, вып. 3. — doi:10.2307/2319844. — JSTOR 2319844.
  • Heinrich Tietze. Einige Bemerkungen zum Problem des Kartenfärbens auf einseitigen Flächen (Some remarks on the problem of map coloring on one-sided surfaces) // DMV Annual Report. — 1910. — Т. 19. (недоступная ссылка)
  • L. Clark, R. Entringer. Smallest maximally nonhamiltonian graphs // Periodica Mathematica Hungarica. — 1983. — Т. 14, вып. 1. — doi:10.1007/BF02023582.
  • L. Esperet, G. Mazzuoccolo. On cubic bridgeless graphs whose edge-set cannot be covered by four perfect matchings // Journal of Graph Theory. — 2014. — Т. 77, вып. 2. — doi:10.1002/jgt.21778. — arXiv:1301.6926.
Источник — https://ru.wikipedia.org/ruwiki/w/index.php?title=Граф_Титце&oldid=141437144