Закон Ома: различия между версиями
| [отпатрулированная версия] | [непроверенная версия] |
Jaguar K (обсуждение | вклад) м →История |
|||
| (не показаны 4 промежуточные версии 3 участников) | |||
| Строка 2: | Строка 2: | ||
{{Электродинамика}} |
{{Электродинамика}} |
||
[[Файл:UIR.svg|right|thumb|200px|{{math|''U''}} — напряжение,<br> {{math|''I''}} — сила тока,<br> {{math|''R''}} — сопротивление]] |
[[Файл:UIR.svg|right|thumb|200px|{{math|''U''}} — напряжение,<br> {{math|''I''}} — сила тока,<br> {{math|''R''}} — сопротивление]] |
||
'''Зако́н О́ма''' |
'''Зако́н О́ма''' описывает линейную зависимость между [[Сила тока|силой тока]] на участке цепи и [[Электрическое напряжение|электрическим напряжением]] на этом участке. Установлен [[Ом, Георг Симон|Георгом Омом]] в 1826 году (опубликован в [[1827 год в науке|1827 году]]) и назван в его честь. Для участка цепи закон Ома выражается формулой<ref name=":1">{{Cite web|lang=ru|url=https://old.bigenc.ru/physics/text/2686298|title=Закон Ома|author=Ю. В. Юрьев|website=Большая Российская Энциклопедия|access-date=2023-06-15|archive-date=2023-02-21|archive-url=https://web.archive.org/web/20230221173523/https://old.bigenc.ru/physics/text/2686298|deadlink=no}}</ref> : |
||
: <math>I\! = {U \over R} </math>, где |
|||
В своей работе<ref>[http://www.th-nuernberg.de/institutionen/bibliothek/elektronische-angebote/historische-quellen-am-ohm/werke-von-georg-simon-ohm/die-galvanische-kette/page.html G. S. Ohm (1827). Die galvanische Kette, mathematisch bearbeitet. Berlin: T. H. Riemann.] {{Wayback|url=http://www.th-nuernberg.de/institutionen/bibliothek/elektronische-angebote/historische-quellen-am-ohm/werke-von-georg-simon-ohm/die-galvanische-kette/page.html |date=20170315001415 }}</ref> Ом записал закон в следующем виде: |
|||
: <math> X\! = {a \over {b+l}}, \qquad(1)</math> |
|||
где: |
|||
* {{math|''X''}} — показания [[гальванометр]]а (в современных обозначениях, сила тока {{math|''I''}}); |
|||
* {{math|''a''}} — величина, характеризующая свойства источника напряжения, постоянная в широких пределах и не зависящая от величины тока (в современной терминологии, [[электродвижущая сила]] (ЭДС) {{math|ε}}); |
|||
* {{math|''l''}} — величина, определяемая длиной соединяющих проводов (в современных представлениях соответствует сопротивлению внешней цепи {{math|''R''}}); |
|||
* {{math|''b''}} — параметр, характеризующий свойства всей электрической установки (в современных представлениях, параметр, в котором можно усмотреть учёт внутреннего сопротивления источника тока {{math|''r''}}). |
|||
Формула (1) при использовании современных терминов выражает '''закон Ома для полной цепи''': |
|||
: <math>I \! = { \varepsilon \! \over {R+r} }, \qquad(2)</math> |
|||
где: |
|||
* <math> {\varepsilon\!} </math> — [[Электродвижущая сила|ЭДС]] [[источник напряжения|источника напряжения]], [[Вольт (единица измерения)|В]]; |
|||
* <math>I</math> — [[сила тока]] в цепи, [[Ампер (единица измерения)|А]]; |
* <math>I</math> — [[сила тока]] в цепи, [[Ампер (единица измерения)|А]]; |
||
* <math> |
* <math>U</math> — [[электрическое напряжение]] на участке цепи, [[Вольт|В]]; |
||
* <math> |
* <math>R</math> — [[электрическое сопротивление]] участка цепи, [[Ом (единица измерения)|Ом]]; |
||
Вербальная формулировка закона Ома: |
|||
Из закона Ома для полной цепи вытекают следующие следствия: |
|||
* при <math>r\ll R</math> сила тока в цепи обратно пропорциональна её сопротивлению, а сам источник в ряде случаев может быть назван [[Источник ЭДС|источником напряжения]]; |
|||
* при <math>r\gg R</math> сила тока не зависит от свойств внешней цепи (от величины нагрузки), и источник может быть назван [[Источник тока|источником тока]]. |
|||
{{цитата|Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи.}} |
|||
Часто<ref>Преимущественно в школьных учебниках и научно-популярной литературе.</ref> выражение |
|||
Другая форма записи закона Ома<ref name=":1" /><ref name=":2">{{Книга|автор=Д. В. Сивухин|заглавие=Общий курс физики. Учеб. пособие: Для вузов. В 5 т. Т. III. Электричество|год=2004|место=Москва|издательство=Физматлит: издательство МФТИ|страницы=194|isbn=5-9221-0227-3}}</ref> использует определение [[Электрическое напряжение|электрического напряжения]]<ref>{{Cite web|lang=ru|url=https://old.bigenc.ru/physics/text/2248704|title=Электрическое напряжение|author=Ю. В. Юрьев|website=Большая российская энциклопедия|access-date=2023-06-15|archive-date=2023-02-21|archive-url=https://web.archive.org/web/20230221185747/https://old.bigenc.ru/physics/text/2248704|deadlink=no}}</ref> как суммы [[Электродвижущая сила|ЭДС]], действующей на выбранном участке между двумя точками, и разности [[Электростатический потенциал|потенциалов]] между этими точками. Это также называют '''законом Ома для участка цепи''': |
|||
: <math> U\! = IR, \qquad(3) </math> |
|||
: <math>IR = \varphi_1 - \varphi_2 + \mathcal {E}_{12} </math> |
|||
где <math>U</math> есть [[Электрическое напряжение|напряжение]], или [[падение напряжения]] (или, что то же, [[разность потенциалов]] между началом и концом участка проводника), тоже называют «законом Ома». |
|||
Для замкнутого участка цепи (точки 1 и 2 совпадают) формула, приведённая выше, упрощается<ref name=":1" /><ref name=":2" />: |
|||
Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется: |
|||
: <math> |
: <math>IR = \mathcal {E}_{12} </math> |
||
== Области применения == |
|||
То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему ''замкнутой'' цепи. В таком случае оно всегда меньше ЭДС. |
|||
Закон Ома в [[электродинамика сплошных сред|электродинамике сплошных сред]] и в [[Теория электрических цепей|теории электрических цепей]] имеет несколько разный смысл и область применения. |
|||
В [[Физика|физике]] закон Ома — изначально [[Эмпирическая формула (познание)|эмпирическое]] соотношение, которое было впоследствии объяснено [[Теория Друде|теорией Друде]] о движении электронов в металлах. Это соотношение хорошо описывает часто встречаемые на практике типы проводников в [[Квазистационарные поля|квазистационарном приближении]], но не является фундаментальным физическим законом и перестаёт соблюдаться в ряде ситуаций. |
|||
К другой записи формулы (3), а именно: |
|||
В [[Теория электрических цепей|теории электрических цепей]] закон Ома [[Аксиоматический метод|аксиоматически]] определяет связь параметров напряжения и тока в модели электрической цепи через параметр электрического сопротивления (или, в общем случае, через параметр комплексного [[Электрический импеданс|импеданса]]). Существуют законы Ома для комплексных амплитуд и для комплексных [[Действующее значение переменного тока|действующих значений]]<ref>{{Книга|автор=Матвиенко В.А.|заглавие=Основы теории цепей : учебное пособие для вузов|год=2016|место=Екатеринбург|издательство=УМЦ УПИ|страницы=52|isbn=978-5-8295-0425-0}}</ref>. |
|||
: <math>I\! = {U \over R} \qquad(5) </math> |
|||
== История == |
|||
применима другая формулировка: {{цитата|Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи.}} |
|||
В 1825—1827 годах [[Ом, Георг Симон|Георг Ом]] проводил опыты с [[Источник ЭДС|источником ЭДС]] в виде [[Термопара|термопары]], [[гальванометр]]ом и металлической проволокой. Он обнаружил, что [[сила тока]] через проволоку в его опытах хорошо описывается линейным законом на основе трёх параметров, и в 1827 году опубликовал результаты в виде работы ''Die galvanische Kette, mathematisch bearbeitet''<ref name=":0">{{cite web |url = http://www.th-nuernberg.de/institutionen/bibliothek/elektronische-angebote/historische-quellen-am-ohm/werke-von-georg-simon-ohm/die-galvanische-kette/page.html |title = G. S. Ohm (1827). Die galvanische Kette, mathematisch bearbeitet. Berlin: T. H. Riemann. |archive-url = https://web.archive.org/web/20170315001415/http://www.th-nuernberg.de/institutionen/bibliothek/elektronische-angebote/historische-quellen-am-ohm/werke-von-georg-simon-ohm/die-galvanische-kette/page.html |archive-date = 2017-03-15 }}</ref>. Опыты Георга Ома проводились до зарождения [[Теория электрических цепей|теории цепей]] и [[Правила Кирхгофа|правил Кирхгофа]] (1845—1847), теории [[Электромагнитное поле|электромагнитного поля]] (1864), [[Уравнения Максвелла|уравнений Максвелла]] (1884), и [[Теория Друде|теории Друде]] (1900). В его работе закон Ома был записан как выражение |
|||
: <math>S = \frac{a}{b + x} </math>, где: |
|||
Выражение (5) можно переписать в виде |
|||
* <math>S </math> — показания [[гальванометр]]а (в современных терминах — сила тока); |
|||
* <math>a </math> — величина, характеризующая свойства источника напряжения, постоянная в широких пределах и не зависящая от величины тока (в современных терминах — [[Электродвижущая сила|ЭДС]]); |
|||
* <math>b </math> — параметр, характеризующий свойства всей электрической установки (в современных представлениях, параметр, в котором можно усмотреть учёт внутреннего сопротивления источника тока {{math|''r''}}). |
|||
* <math>x </math> — величина, определяемая длиной соединяющих проводов (в современных представлениях соответствует сопротивлению внешней цепи {{math|''R''}}). |
|||
Позднее, в 1845—1849 годах [[Кирхгоф, Густав|Густав Кирхгоф]] предложил корректную физическую интерпретацию этих величин, и в 1849 году опубликовал работу, включающую в себя закон Ома в современных единицах<ref>{{Книга|автор=Franco Maloberti, Anthony C. Davies|заглавие=A Short History of Circuits and Systems|год=2016|место=Denmark|издательство=River Publishers|isbn=978-87-93379-70-1}}</ref>. |
|||
: <math>I\! = {U G}, \qquad(6) </math> |
|||
Оригинальная формула при использовании современных терминов выражает так называемый '''закон Ома для полной цепи''': |
|||
где коэффициент пропорциональности {{math|''G''}} назван [[проводимость]] или [[электропроводность]]. Изначально единицей измерения проводимости был «обратный ом» — Мо<ref>{{Книга:БЭС |Мо|39422}}</ref>, в [[СИ|Международной системе единиц (СИ)]] единицей измерения проводимости является '''[[Сименс (единица измерения)|си́менс]]''' (русское обозначение: '''См'''; международное: '''S'''), величина которого равна обратному ому. |
|||
: <math>I \! = { \mathcal {E} \! \over {R+r} }</math>, где: |
|||
== Мнемоническая диаграмма для закона Ома == |
|||
* <math> {\mathcal {E}} </math> — [[Электродвижущая сила|ЭДС]] источника, [[Вольт (единица измерения)|В]]; |
|||
[[Файл:Ohm's Law with Voltage source ru.svg|thumb|right|250px|Схема, иллюстрирующая три составляющие закона Ома]] |
|||
* <math>I</math> — [[сила тока]] в цепи, [[Ампер (единица измерения)|А]]; |
|||
[[Файл:Ohm's law triangle.PNG|thumb|right|250px|Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления]] |
|||
* <math>R</math> — [[электрическое сопротивление|сопротивление]] всех элементов цепи (не включая источник ЭДС), [[Ом (единица измерения)|Ом]]; |
|||
[[Файл:Закон Ома (перерисованный).png|thumb|right|250px|{{math|''U''}} — [[электрическое напряжение]];<br>{{math|''I''}} — [[сила тока]];<br>{{math|''P''}} — [[электрическая мощность]];<br>{{math|''R''}} — [[электрическое сопротивление]]]] |
|||
* <math>r</math> — [[внутреннее сопротивление]] источника ЭДС, [[Ом (единица измерения)|Ом]]. |
|||
В соответствии с этой диаграммой формально может быть записано выражение: |
|||
: <math>R\!= {U \over I}, \qquad(7)</math> |
|||
которое всего лишь позволяет вычислить (применительно к известному току, создающему на заданном участке цепи известное напряжение), сопротивление этого участка. Но математически корректное утверждение о том, что сопротивление проводника растёт прямо пропорционально приложенному к нему напряжению и обратно пропорционально пропускаемому через него току, физически ложно. |
|||
В специально оговорённых случаях сопротивление может зависеть от этих величин, но по умолчанию оно определяется лишь физическими и геометрическими параметрами проводника: |
|||
: <math>R\!= {\varrho l \over s}, \qquad(8) </math> |
|||
== Закон Ома в дифференциальной форме == |
|||
{{Основная статья|Теория Друде}} |
|||
Линейная связь плотности тока и напряжённости электрического поля в некоторой точке проводника описывается законом Ома в дифференциальной форме. Коэффициентом пропорциональности является удельная проводимость материала. Для [[Изотропия|изотропных]] материалов дифференциальная форма закона Ома выглядит как: |
|||
: <math>\vec j = \sigma \vec {E},</math> |
|||
где: |
где: |
||
* <math>\vec j</math> — вектор [[плотность тока|плотности тока]]; |
|||
* <math>\varrho</math> — удельное электрическое сопротивление материала, из которого сделан проводник, |
|||
* <math>\sigma</math> — [[удельная проводимость|удельная электрическая проводимость]] (<math>\sigma = 1 / \rho</math>); |
|||
* <math>l</math> — его длина |
|||
* <math>\vec E</math> — вектор [[напряжённость электрического поля|напряжённости электрического поля]]. |
|||
* <math>s</math> — площадь его поперечного сечения |
|||
Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. |
|||
=== Закон Ома и ЛЭП === |
|||
Одним из важнейших требований к линиям электропередачи (ЛЭП) является уменьшение потерь при доставке энергии потребителю. Эти потери в настоящее время заключаются в нагреве проводов, то есть переходе энергии тока в тепловую энергию, за что ответственно омическое сопротивление проводов. Иными словами, задача состоит в том, чтобы довести до потребителя как можно более значительную часть мощности источника тока <math>P</math> = <math> {\varepsilon\! I\!} </math> при минимальных потерях мощности в линии передачи <math>P (r) = UI, </math> где <math>U\! = Ir ,</math> причём <math>r</math> на этот раз есть суммарное сопротивление проводов и внутреннего сопротивления генератора (последнее всё же меньше сопротивления линии передач). |
|||
В классическом приближении закон Ома в дифференциальной форме можно вывести с использованием [[теория Друде|теории Друде]]: |
|||
В таком случае потери мощности будут определяться выражением |
|||
: <math>\vec j=\frac{n \cdot e_0^{2}\cdot\tau}{2m} \cdot\vec E=\sigma\vec E,</math> |
|||
: <math>P(r) = \frac{P^2 r}{\varepsilon ^2}. \qquad(9) </math> |
|||
Отсюда следует, что при постоянной передаваемой мощности её потери растут прямо пропорционально длине ЛЭП и обратно пропорционально квадрату ЭДС. Таким образом, желательно всемерное увеличение ЭДС. Однако ЭДС ограничивается электрической прочностью обмотки генератора, поэтому повышать напряжение на входе линии следует уже после выхода тока из генератора, что для постоянного тока является проблемой. Однако для переменного тока эта задача много проще решается с помощью использования [[трансформатор]]ов, что и предопределило повсеместное распространение ЛЭП на переменном токе. Однако при повышении напряжения в линии возникают потери на [[коронный разряд|коронирование]] и возникают трудности с обеспечением надёжности изоляции от земной поверхности. Поэтому наибольшее практически используемое напряжение в дальних ЛЭП обычно не превышает миллиона вольт. |
|||
Кроме того, любой проводник, как показал [[Максвелл, Джеймс Клерк|Дж. Максвелл]], при изменении силы тока в нём излучает энергию в окружающее пространство, и потому ЛЭП ведёт себя как [[антенна]], что заставляет в ряде случаев наряду с омическими потерями брать в расчёт и потери на излучение. |
|||
== Закон Ома в дифференциальной форме == |
|||
Сопротивление <math>R</math> зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника. |
|||
Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для [[Изотропия|изотропных]] материалов имеем: |
|||
: <math>\mathbf{J} = \sigma \mathbf{E},</math> |
|||
где: |
где: |
||
* <math>\mathbf{J}</math> — вектор [[плотность тока|плотности тока]], |
|||
* <math>\sigma</math> — [[Электрическая проводимость|удельная проводимость]], |
|||
* <math>\mathbf{E}</math> — вектор [[напряжённость электрического поля|напряжённости электрического поля]]. |
|||
* <math>\sigma</math> — [[удельная проводимость|удельная электрическая проводимость]] (<math>\sigma = 1 / \rho</math>); |
|||
Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал [[Анизотропия|анизотропен]], то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость <math>\sigma_{ij}</math> является симметричным [[тензор]]ом ранга (1, 1), а закон Ома, записанный в дифференциальной форме, приобретает вид |
|||
* <math>n</math> — [[Концентрация частиц|концентрация]] электронов; |
|||
* <math>e_0</math> — [[элементарный заряд]]; |
|||
: <math>J_i = \sum_{j=1}^3\sigma_{ij}E_j.</math> |
|||
* <math>\tau</math> — [[время релаксации]] по [[импульс]]ам (время, за которое электрон «''забывает''» о том, в какую сторону двигался); |
|||
* <math>m</math> — [[тензор эффективной массы|эффективная масса]] электрона. |
|||
Раздел [[физика|физики]], изучающий течение электрического тока (и другие электромагнитные явления) в различных средах, называется [[электродинамика сплошных сред|электродинамикой сплошных сред]]. |
|||
== Закон Ома для переменного тока == |
== Закон Ома для переменного тока == |
||
В [[Теория электрических цепей|теории электрических цепей]] закон Ома обобщается для [[Переменный ток|переменного тока]]. Специальному рассмотрению подлежит лишь учёт [[сдвиг фаз|фазового сдвига]] между током и напряжением. Если ток является синусоидальным с [[циклическая частота|циклической частотой]] {{math|ω}}, а цепь содержит не только активные, но и реактивные компоненты ([[Электрическая ёмкость|ёмкости]], [[индуктивность|индуктивности]]), закон Ома может быть записан в [[комплексные числа|комплексных]] величинах: |
|||
Вышеприведённые соображения о свойствах электрической цепи при использовании источника (генератора) с переменной во времени ЭДС остаются справедливыми. Специальному рассмотрению подлежит лишь учёт специфических свойств потребителя, приводящих к разновременности достижения напряжением и током своих максимальных значений, то есть учёт [[сдвиг фаз|фазового сдвига]]. |
|||
: <math>\mathbb{I} = \frac {\mathbb{U}} {\mathbb{Z}} ,</math> |
|||
Если ток является синусоидальным с [[циклическая частота|циклической частотой]] {{math|ω}}, а цепь содержит не только активные, но и реактивные компоненты ([[Электрическая ёмкость|ёмкости]], [[индуктивность|индуктивности]]), то закон Ома обобщается; величины, входящие в него, становятся [[комплексные числа|комплексными]]: |
|||
: <math>\mathbb{U} = \mathbb{I} \cdot \mathbb{Z},</math> |
|||
где: |
где: |
||
* <math>\mathbb{U} = U_0 e^{i\omega t} </math> — комплексное напряжение |
* <math>\mathbb{U} = U_0 e^{i\omega t} </math> — комплексное напряжение, |
||
* <math>\mathbb{I} </math> — комплексная сила тока, |
* <math>\mathbb{I} </math> — комплексная сила тока, |
||
* <math>\mathbb{Z} = R e^{-i\delta} </math> — комплексное сопротивление ([[электрический импеданс]]), |
* <math>\mathbb{Z} = R e^{-i\delta} </math> — комплексное сопротивление ([[электрический импеданс]]), |
||
| Строка 115: | Строка 84: | ||
При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведён взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, <math>U=U_0\sin(\omega t+\varphi)</math> подбором такой <math>\mathbb{U}=U_0e^{i(\omega t + \varphi)},</math> что <math>\operatorname{Im} \mathbb{U} = U. </math> Тогда все значения токов и напряжений в схеме надо считать как <math>F=\operatorname{Im} \mathbb{F}.</math> |
При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведён взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, <math>U=U_0\sin(\omega t+\varphi)</math> подбором такой <math>\mathbb{U}=U_0e^{i(\omega t + \varphi)},</math> что <math>\operatorname{Im} \mathbb{U} = U. </math> Тогда все значения токов и напряжений в схеме надо считать как <math>F=\operatorname{Im} \mathbb{F}.</math> |
||
Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных [[Фурье-анализ|Фурье-компонент]]. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо. Нелинейность цепи приводит к возникновению |
Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных [[Фурье-анализ|Фурье-компонент]]. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо. Нелинейность цепи приводит к возникновению гармоник (колебаний с частотой, кратной частоте тока, действующего на цепь), а также колебаний с суммарными и разностными частотами. Вследствие этого закон Ома в нелинейных цепях, вообще говоря, не выполняется. |
||
== |
== Мнемоническая диаграмма для закона Ома == |
||
[[Файл:Ohm's law triangle.PNG|thumb|right|250px|Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления]] |
|||
Закон Ома, в отличие от, например, [[Закон Кулона|закона Кулона]], является не фундаментальным физическим законом, а лишь эмпирическим соотношением, хорошо описывающим наиболее часто встречаемые на практике типы проводников в приближении небольших [[Частота|частот]], [[Плотность тока|плотностей тока]] и [[Напряжённость электрического поля|напряжённостей электрического поля]], но перестающим соблюдаться в ряде ситуаций. |
|||
[[Файл:Закон Ома (перерисованный).png|thumb|right|250px|{{math|''U''}} — [[электрическое напряжение]];<br>{{math|''I''}} — [[сила тока]];<br>{{math|''P''}} — [[электрическая мощность]];<br>{{math|''R''}} — [[электрическое сопротивление]]]] |
|||
Мнемоническая диаграмма позволяет получить выражение для необходимой величины из формулы закона Ома. |
|||
== Практическое значение закона Ома == |
|||
В классическом приближении закон Ома можно вывести при помощи [[теория Друде|теории Друде]]: |
|||
Одним из важнейших требований к линиям электропередачи (ЛЭП) является уменьшение потерь при доставке энергии потребителю. Эти потери в настоящее время заключаются в нагреве проводов, то есть переходе энергии тока в тепловую энергию, за что ответственно омическое сопротивление проводов. Иными словами, задача состоит в том, чтобы довести до потребителя как можно более значительную часть мощности источника тока <math>P</math> = <math> {\varepsilon\! I\!} </math> при минимальных потерях мощности в линии передачи <math>P (r) = UI, </math> где <math>U\! = Ir ,</math> причём <math>r</math> на этот раз есть суммарное сопротивление проводов и внутреннего сопротивления генератора (последнее всё же меньше сопротивления линии передач). |
|||
: <math>\mathbf{J}=\frac{n \cdot e_0^{2}\cdot\tau}{m} \cdot\mathbf{E}=\sigma\cdot\mathbf{E}.</math> |
|||
В таком случае потери мощности будут определяться выражением |
|||
Здесь: |
|||
: <math>P(r) = \frac{P^2 r}{\varepsilon ^2}. </math> |
|||
* <math>\sigma</math> — электрическая [[удельная проводимость]]; |
|||
* <math>n</math> — [[Концентрация частиц|концентрация]] электронов; |
|||
* <math>e_0</math> — [[элементарный заряд]]; |
|||
* <math>\tau</math> — [[время релаксации]] по [[импульс]]ам (время, за которое электрон «''забывает''» о том, в какую сторону двигался); |
|||
* <math>m</math> — [[тензор эффективной массы|эффективная масса]] электрона. |
|||
Отсюда следует, что при постоянной передаваемой мощности её потери растут прямо пропорционально длине ЛЭП и обратно пропорционально квадрату ЭДС. Таким образом, желательно всемерное увеличение ЭДС. Однако ЭДС ограничивается электрической прочностью обмотки генератора, поэтому повышать напряжение на входе линии следует уже после выхода тока из генератора, что для постоянного тока является проблемой. Однако для переменного тока эта задача много проще решается с помощью использования [[трансформатор]]ов, что и предопределило повсеместное распространение ЛЭП на переменном токе. Однако при повышении напряжения в линии возникают потери на [[коронный разряд|коронирование]] и возникают трудности с обеспечением надёжности изоляции от земной поверхности. Поэтому наибольшее практически используемое напряжение в дальних ЛЭП обычно не превышает миллиона вольт. |
|||
Проводники и элементы, для которых соблюдается закон Ома, называются омическими. |
|||
Кроме того, любой проводник, как показал [[Максвелл, Джеймс Клерк|Дж. Максвелл]], при изменении силы тока в нём излучает энергию в окружающее пространство, и потому ЛЭП ведёт себя как [[антенна]], что заставляет в ряде случаев наряду с омическими потерями брать в расчёт и потери на излучение. |
|||
== Ограничения применимости закона Ома == |
|||
Закон Ома может не соблюдаться: |
|||
Закон Ома (как физический закон) может не соблюдаться: |
|||
* Для любых сред, к которым не применима [[теория Друде]] (например, [[плазма]] или [[вакуум]]) |
|||
* При высоких частотах, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда. |
* При высоких частотах, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда. |
||
* При низких температурах для веществ, обладающих [[сверхпроводимость]]ю. |
* При низких температурах для веществ, обладающих [[сверхпроводимость]]ю. |
||
Текущая версия от 07:19, 3 октября 2023

I — сила тока,
R — сопротивление
Зако́н О́ма описывает линейную зависимость между силой тока на участке цепи и электрическим напряжением на этом участке. Установлен Георгом Омом в 1826 году (опубликован в 1827 году) и назван в его честь. Для участка цепи закон Ома выражается формулой[1] :
- , где
- — сила тока в цепи, А;
- — электрическое напряжение на участке цепи, В;
- — электрическое сопротивление участка цепи, Ом;
Вербальная формулировка закона Ома:
Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи.
Другая форма записи закона Ома[1][2] использует определение электрического напряжения[3] как суммы ЭДС, действующей на выбранном участке между двумя точками, и разности потенциалов между этими точками. Это также называют законом Ома для участка цепи:
Для замкнутого участка цепи (точки 1 и 2 совпадают) формула, приведённая выше, упрощается[1][2]:
Области применения
Закон Ома в электродинамике сплошных сред и в теории электрических цепей имеет несколько разный смысл и область применения.
В физике закон Ома — изначально эмпирическое соотношение, которое было впоследствии объяснено теорией Друде о движении электронов в металлах. Это соотношение хорошо описывает часто встречаемые на практике типы проводников в квазистационарном приближении, но не является фундаментальным физическим законом и перестаёт соблюдаться в ряде ситуаций.
В теории электрических цепей закон Ома аксиоматически определяет связь параметров напряжения и тока в модели электрической цепи через параметр электрического сопротивления (или, в общем случае, через параметр комплексного импеданса). Существуют законы Ома для комплексных амплитуд и для комплексных действующих значений[4].
История
В 1825—1827 годах Георг Ом проводил опыты с источником ЭДС в виде термопары, гальванометром и металлической проволокой. Он обнаружил, что сила тока через проволоку в его опытах хорошо описывается линейным законом на основе трёх параметров, и в 1827 году опубликовал результаты в виде работы Die galvanische Kette, mathematisch bearbeitet[5]. Опыты Георга Ома проводились до зарождения теории цепей и правил Кирхгофа (1845—1847), теории электромагнитного поля (1864), уравнений Максвелла (1884), и теории Друде (1900). В его работе закон Ома был записан как выражение
- , где:
- — показания гальванометра (в современных терминах — сила тока);
- — величина, характеризующая свойства источника напряжения, постоянная в широких пределах и не зависящая от величины тока (в современных терминах — ЭДС);
- — параметр, характеризующий свойства всей электрической установки (в современных представлениях, параметр, в котором можно усмотреть учёт внутреннего сопротивления источника тока r).
- — величина, определяемая длиной соединяющих проводов (в современных представлениях соответствует сопротивлению внешней цепи R).
Позднее, в 1845—1849 годах Густав Кирхгоф предложил корректную физическую интерпретацию этих величин, и в 1849 году опубликовал работу, включающую в себя закон Ома в современных единицах[6].
Оригинальная формула при использовании современных терминов выражает так называемый закон Ома для полной цепи:
- , где:
- — ЭДС источника, В;
- — сила тока в цепи, А;
- — сопротивление всех элементов цепи (не включая источник ЭДС), Ом;
- — внутреннее сопротивление источника ЭДС, Ом.
Закон Ома в дифференциальной форме
Линейная связь плотности тока и напряжённости электрического поля в некоторой точке проводника описывается законом Ома в дифференциальной форме. Коэффициентом пропорциональности является удельная проводимость материала. Для изотропных материалов дифференциальная форма закона Ома выглядит как:
где:
- — вектор плотности тока;
- — удельная электрическая проводимость ();
- — вектор напряжённости электрического поля.
Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени.
В классическом приближении закон Ома в дифференциальной форме можно вывести с использованием теории Друде:
где:
- — удельная электрическая проводимость ();
- — концентрация электронов;
- — элементарный заряд;
- — время релаксации по импульсам (время, за которое электрон «забывает» о том, в какую сторону двигался);
- — эффективная масса электрона.
Закон Ома для переменного тока
В теории электрических цепей закон Ома обобщается для переменного тока. Специальному рассмотрению подлежит лишь учёт фазового сдвига между током и напряжением. Если ток является синусоидальным с циклической частотой ω, а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), закон Ома может быть записан в комплексных величинах:
где:
- — комплексное напряжение,
- — комплексная сила тока,
- — комплексное сопротивление (электрический импеданс),
- R = √Ra2 + Rr2 — полное сопротивление (модуль импеданса),
- Rr = ωL − 1/(ωC) — реактивное сопротивление (разность индуктивного и емкостного),
- Rа — активное (омическое) сопротивление, не зависящее от частоты,
- δ = − arctg (Rr/Ra) — сдвиг фаз между напряжением и силой тока (фаза импеданса, с точностью до обратного знака).
При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведён взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, подбором такой что Тогда все значения токов и напряжений в схеме надо считать как
Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо. Нелинейность цепи приводит к возникновению гармоник (колебаний с частотой, кратной частоте тока, действующего на цепь), а также колебаний с суммарными и разностными частотами. Вследствие этого закон Ома в нелинейных цепях, вообще говоря, не выполняется.
Мнемоническая диаграмма для закона Ома
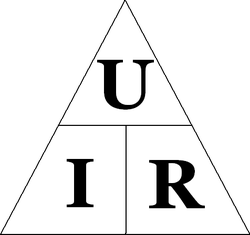

I — сила тока;
P — электрическая мощность;
R — электрическое сопротивление
Мнемоническая диаграмма позволяет получить выражение для необходимой величины из формулы закона Ома.
Практическое значение закона Ома
Одним из важнейших требований к линиям электропередачи (ЛЭП) является уменьшение потерь при доставке энергии потребителю. Эти потери в настоящее время заключаются в нагреве проводов, то есть переходе энергии тока в тепловую энергию, за что ответственно омическое сопротивление проводов. Иными словами, задача состоит в том, чтобы довести до потребителя как можно более значительную часть мощности источника тока = при минимальных потерях мощности в линии передачи где причём на этот раз есть суммарное сопротивление проводов и внутреннего сопротивления генератора (последнее всё же меньше сопротивления линии передач).
В таком случае потери мощности будут определяться выражением
Отсюда следует, что при постоянной передаваемой мощности её потери растут прямо пропорционально длине ЛЭП и обратно пропорционально квадрату ЭДС. Таким образом, желательно всемерное увеличение ЭДС. Однако ЭДС ограничивается электрической прочностью обмотки генератора, поэтому повышать напряжение на входе линии следует уже после выхода тока из генератора, что для постоянного тока является проблемой. Однако для переменного тока эта задача много проще решается с помощью использования трансформаторов, что и предопределило повсеместное распространение ЛЭП на переменном токе. Однако при повышении напряжения в линии возникают потери на коронирование и возникают трудности с обеспечением надёжности изоляции от земной поверхности. Поэтому наибольшее практически используемое напряжение в дальних ЛЭП обычно не превышает миллиона вольт.
Кроме того, любой проводник, как показал Дж. Максвелл, при изменении силы тока в нём излучает энергию в окружающее пространство, и потому ЛЭП ведёт себя как антенна, что заставляет в ряде случаев наряду с омическими потерями брать в расчёт и потери на излучение.
Ограничения применимости закона Ома
Закон Ома (как физический закон) может не соблюдаться:
- Для любых сред, к которым не применима теория Друде (например, плазма или вакуум)
- При высоких частотах, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.
- При низких температурах для веществ, обладающих сверхпроводимостью.
- При заметном нагреве проводника проходящим током, в результате чего зависимость напряжения от тока (вольт-амперная характеристика) приобретает нелинейный характер. Классическим примером такого элемента является лампа накаливания.
- При приложении к проводнику или диэлектрику (например, воздуху или изоляционной оболочке) высокого напряжения, вследствие чего возникает пробой.
- В вакуумных и газонаполненных электронных лампах (в том числе люминесцентных).
- В гетерогенных полупроводниках и полупроводниковых приборах, имеющих p-n-переходы, например, в диодах и транзисторах.
- В контактах металл-диэлектрик (вследствие образования пространственного заряда в диэлектрике)[7].
Примечания
- ↑ 1 2 3 Ю. В. Юрьев. Закон Ома. Большая Российская Энциклопедия. Дата обращения: 15 июня 2023. Архивировано 21 февраля 2023 года.
- ↑ 1 2 Д. В. Сивухин. Общий курс физики. Учеб. пособие: Для вузов. В 5 т. Т. III. Электричество. — Москва: Физматлит: издательство МФТИ, 2004. — С. 194. — ISBN 5-9221-0227-3.
- ↑ Ю. В. Юрьев. Электрическое напряжение. Большая российская энциклопедия. Дата обращения: 15 июня 2023. Архивировано 21 февраля 2023 года.
- ↑ Матвиенко В.А. Основы теории цепей : учебное пособие для вузов. — Екатеринбург: УМЦ УПИ, 2016. — С. 52. — ISBN 978-5-8295-0425-0.
- ↑ G. S. Ohm (1827). Die galvanische Kette, mathematisch bearbeitet. Berlin: T. H. Riemann. Архивировано 15 марта 2017 года.
- ↑ Franco Maloberti, Anthony C. Davies. A Short History of Circuits and Systems. — Denmark: River Publishers, 2016. — ISBN 978-87-93379-70-1.
- ↑ Рез И. С., Поплавко Ю. М. Диэлектрики. Основные свойства и применения в электронике. — М., Радио и связь, 1989, — с. 46-51
Ссылки
- Закон Ома // Элементы.ru. Природа науки, Энциклопедия





































