Парадокс Симпсона: различия между версиями
| [непроверенная версия] | [непроверенная версия] |
Нет описания правки |
MahSim (обсуждение | вклад) →Практическая значимость: Упростил формулировки, добавил что устранять нужно систематические перекосы |
||
| (не показана 41 промежуточная версия 33 участников) | |||
| Строка 1: | Строка 1: | ||
[[Файл:Simpson's paradox continuous.svg|thumb| Парадокс Симпсона для количественных данных: для каждой из групп в отдельности проявляется положительная тенденция (<span style="display:inline-block; vertical-align:middle; width:2em; height:0px; border-style:none; border-top:2px solid blue;"> </span>, <span style="display:inline-block; vertical-align:middle; width:2em; height:0px; border-style:none; border-top:2px solid red;"> </span>), тогда как для их объединения имеет место отрицательная (<span style="display:inline-block; vertical-align:middle; width:2em; height:0px; border-style:none; border-top:2px dashed #000;"> </span>).]] |
|||
| ⚫ | |||
| ⚫ | '''Парадокс Симпсона''' (также '''Парадокс Юла — Симпсона''' или '''парадокс объединения''') — явление в статистике, когда при наличии двух групп данных, в каждой из которых наблюдается одинаково направленная зависимость, при объединении этих групп направление зависимости меняется на противоположное. |
||
| ⚫ | Это явление было описано |
||
Например, подсчёты по некоторой группе людей могут говорить, что определённое лекарство увеличивает шанс выздоровления, и при этом если разделить группу на две (мужчин и женщин), то оказывается, что это лекарство уменьшает шанс выздоровления в каждой группе. |
|||
| ⚫ | |||
Однако, так как Симпсон не был первооткрывателем этого эффекта, некоторые авторы используют безличные названия, например, «[[парадокс]] объединения». |
|||
== История открытия парадокса == |
== История открытия парадокса == |
||
Первый раз рассматриваемая ситуация отмечена Карлом Пирсоном в статье «Математический вклад в теорию эволюции»<ref name="Pearson1899a">Karl Pearson. Mathematical Contributions to the Theory of Evolution. V. On the Reconstruction of the Stature of Prehistoric Races. Phil. Trans. R. Soc. Lond. A. 1899 192:169-244 doi:10.1098/rsta.1899.0004</ref>. Он рассматривает зависимость признаков разнородных групп лошадей. |
Первый раз рассматриваемая ситуация отмечена Карлом Пирсоном в статье «Математический вклад в теорию эволюции»<ref name="Pearson1899a">Karl Pearson. Mathematical Contributions to the Theory of Evolution. V. On the Reconstruction of the Stature of Prehistoric Races. Phil. Trans. R. Soc. Lond. A. 1899 192:169-244 doi:10.1098/rsta.1899.0004</ref>. Он рассматривает зависимость признаков разнородных групп лошадей. Удни Юл делает более подробный анализ подобных популяционных изменений, изучая механизмы наследственности. Симпсон рассматривает то, что он называет «любопытным случаем» в нескольких разделах статьи «The Interpretation of Interaction in Contingency Tables»<ref name="Simpson1">''The Interpretation of Interaction in Contingency Tables'' // Journal of the Royal Statistical Society, B, 13 (1951) — pp. 238—241</ref>. Симпсон был первым автором, изучавшим это явление с точки зрения статистики. Поэтому впоследствии математик К. Р. Блайт в статье «On Simpson’s Paradox and the Sure-Thing Principle»<ref name="Blyth">Blyth, Colin R. ''On Simpson’s Paradox and the Sure-Thing Principle'' // [[Journal of the American Statistical Association]], 67 (1972) — p. 364.</ref> вводит термин «парадокс Симпсона». |
||
== Примеры == |
== Примеры == |
||
| Строка 17: | Строка 21: | ||
Допустим, что вы хотите вытащить цветную фишку. |
Допустим, что вы хотите вытащить цветную фишку. |
||
Если вы находитесь около стола А, то вероятность извлечь цветную фишку из чёрной шляпы равна {{s|5/11 {{=}} 35/77}}, а из серой шляпы на том же столе |
Если вы находитесь около стола А, то вероятность извлечь цветную фишку из чёрной шляпы равна {{s|5/11 {{=}} 35/77}}, а из серой шляпы на том же столе — {{s|3/7 {{=}} 33/77}}; таким образом, цветную фишку больше шансов вытащить из чёрной шляпы, чем из серой. |
||
Если вы находитесь около стола Б, то вероятность извлечь цветную фишку из чёрной шляпы равна {{s|6/9 {{=}} |
Если вы находитесь около стола Б, то вероятность извлечь цветную фишку из чёрной шляпы равна {{s|6/9 {{=}} 84/126}}, а из серой шляпы — {{s|9/14 {{=}} 81/126}}; таким образом, и здесь цветную фишку больше шансов вытащить из чёрной шляпы, чем из серой. |
||
Допустим теперь, что фишки из двух чёрных шляп сложены в одну чёрную шляпу |
Допустим теперь, что фишки из двух чёрных шляп сложены в одну чёрную шляпу, а фишки из двух серых шляп — в одну серую шляпу. На первый взгляд, логично было бы предположить, что вероятность вытащить цветную фишку из чёрной шляпы выше, чем из серой. Но это неверно: |
||
* вероятность вытащить цветную фишку из чёрной шляпы |
* вероятность вытащить цветную фишку из чёрной шляпы равна {{s|11/20 {{=}} 231/420}}, |
||
* вероятность вытащить цветную фишку из серой шляпы |
* вероятность вытащить цветную фишку из серой шляпы равна {{s|12/21 {{=}} 240/420}}, |
||
то есть больше шансов извлечь цветную фишку из серой шляпы, чем из чёрной<ref>{{книга |
|||
|автор = [[Гарднер, Мартин|М. Гарднер]] |
|автор = [[Гарднер, Мартин|М. Гарднер]] |
||
|заглавие = Путешествие во времени |
|заглавие = Путешествие во времени |
||
| Строка 35: | Строка 39: | ||
|isbn = 5-03-001166-8 |
|isbn = 5-03-001166-8 |
||
|часть = Глава 19. Индукция и вероятность |
|часть = Глава 19. Индукция и вероятность |
||
|страницы = |
|страницы = 278—279 |
||
}}</ref>. |
}}</ref>. |
||
=== Пример с камнями === |
=== Пример с камнями === |
||
Пусть мы имеем четыре набора камней. Вероятность вытащить чёрный камень из набора |
Пусть мы имеем четыре набора камней. Вероятность вытащить чёрный камень из набора № 1 выше, чем из набора № 2. В свою очередь, вероятность вытащить чёрный камень из набора № 3 больше, чем из набора № 4. Объединим набор № 1 с набором № 3 (получим набор I), а набор № 2 — с набором № 4 (набор II). [[Интуиция|Интуитивно]] можно ожидать, что вероятность вытащить чёрный камень из набора I будет выше, чем из набора II. Однако в общем случае такое утверждение неверно. |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
Вероятность вытащить чёрный камень из наборов I и II, соответственно: |
Вероятность вытащить чёрный камень из наборов I и II, соответственно: |
||
| ⚫ | |||
Выражение для набора I не всегда больше выражения для набора II; то есть может случится, что |
|||
| ⚫ | |||
: <math>\frac{n_1 + n_3}{m_1 + m_3} < \frac{n_2 + n_4}{m_2 + m_4}.</math> |
|||
Например, при <math>n_1 = 6</math>, <math>m_1 = 13</math>, <math>n_2 = 4</math>, <math>m_2 = 9</math>, <math>n_3 = 6</math>, <math>m_3 = 9</math>, <math>n_4 = 9</math>, <math>m_4 = 14</math>. |
|||
| ⚫ | |||
| ⚫ | |||
== Причины == |
== Причины == |
||
Причина парадокса заключается в некорректном усреднении двух групп данных с различной долей контрольных наблюдений ( |
Причина парадокса заключается в некорректном усреднении двух групп данных с различной долей контрольных наблюдений ([[Репрезентативность|нерепрезентативная]] [[выборка]]). Поскольку интуитивно предполагается, что при применении найденных зависимостей доля контрольных будет одинаковой в обеих группах, а в исходных данных это не выполняется, то к ним нельзя применять арифметическое усреднение. |
||
Для устранения проблемы, при усреднении необходимо использовать веса, устраняющие перекос доли контрольных. Так, в примере с фишками |
Для устранения проблемы, при усреднении необходимо использовать веса, устраняющие перекос доли контрольных. Так, в примере с фишками доля фишек в серой шляпе на столе А — 7 из 18 (39 %), а на столе Б — 14 из 23 (61 %). |
||
Для репрезентативного усреднения шанса вытянуть цветную фишку |
Для репрезентативного усреднения шанса вытянуть цветную фишку достаточно умножить количество фишек обоих цветов в одной из шляп на весовой коэффициент, устраняющий перекос. Например, если вместо одной серой шляпы на столе А поставить две таких же шляпы, то вероятности для каждого стола в отдельности не изменятся, но для объединения столов парадокс будет устранён: вероятность цветной фишки в серой шляпе станет 15/28, то есть меньше, чем из чёрной. |
||
Другой способ разрешения парадокса |
Другой способ разрешения парадокса — использование [[формула полной вероятности|формулы полной вероятности]]. |
||
Парадокс Симпсона показывает, что выводы из результатов социологических опросов с нерепрезентативной выборкой нельзя принимать как неопровержимые, доказанные научным путём. |
Парадокс Симпсона показывает, что выводы из результатов социологических опросов с нерепрезентативной выборкой нельзя принимать как неопровержимые, доказанные научным путём. |
||
== Практическая значимость == |
== Практическая значимость == |
||
Парадокс Симпсона иллюстрирует неправомерность |
Парадокс Симпсона иллюстрирует неправомерность объединений нерепрезентативных выборок без учёта систематического перекоса выборки данных. |
||
Например, в ходе эксперимента в группе мужчин и группе женщин, больных одной и той же болезнью, к стандартному лечению прибавили новый лекарственный препарат. Результат по обеим группам в отдельности подтверждал эффективность нового средства. |
|||
{| class="wikitable" |
{| class="wikitable" |
||
| Строка 89: | Строка 93: | ||
|} |
|} |
||
Интуитивно предполагается, что если в обеих группах прослеживается зависимость, она должна проявиться и при объединении этих групп. Но хотя соотношение выздоровевших и больных среди и женщин, и мужчин, принимавших лекарство, больше чем среди тех из них, кто его не использовал, в связи с нерепрезентативностью контрольной группы в агрегированных данных эта закономерность не сохраняется. |
Интуитивно предполагается, что если в обеих группах прослеживается зависимость, она должна проявиться и при объединении этих групп. Но хотя соотношение выздоровевших и больных среди и женщин, и мужчин, принимавших лекарство, больше, чем среди тех из них, кто его не использовал, в связи с нерепрезентативностью контрольной группы в агрегированных данных эта закономерность не сохраняется. |
||
{| class="wikitable" |
{| class="wikitable" |
||
| Строка 102: | Строка 106: | ||
|} |
|} |
||
Соотношение в агрегированных данных 850/870<480/410, то есть 0,977<1,171 |
Соотношение в агрегированных данных 850/870<480/410, то есть 0,977<1,171, и доля выздоровевших среди принимавших лекарство оказывается меньше той же доли среди не принимавших. |
||
Для устранения парадокса |
Для устранения парадокса нужно обратить внимание, что отношение контрольной группы к группе воздействия в приведённых группах резко различается: у мужчин составляет (80+130)/(700+800) = 14%, а у женщин (400+280)/(150+70) = 309%. |
||
Это явно систематическая погрешность, и для корректного усреднения нужно обеспечить репрезентативность контрольной группы в обеих выборках, введя весовые коэффициенты так, чтобы взвешенная доля контрольных в обеих группах стала одинаковой. В данном случае достаточно повысить вес результата тех редких мужчин, кто не принимал лекарства, в 22.07 раза. |
|||
Измененные таблицы будут выглядеть так: |
|||
{| class="wikitable" |
{| class="wikitable" |
||
|- |
|- |
||
! rowspan="2" | Мужчины !! rowspan="2" | Принимавшие |
|||
| ⚫ | |||
лекарство |
|||
| ⚫ | |||
| ⚫ | |||
|- |
|||
|исходные |
|||
| ⚫ | |||
|- |
|- |
||
| Выздоровевшие || 700 || 80 |
| Выздоровевшие || 700 || 80 |
||
|1765 |
|||
|3988 |
|||
|- |
|- |
||
| Невыздоровевшие || 800 || 130 |
| Невыздоровевшие || 800 || 130 |
||
|2869 |
|||
|6480.5 |
|||
|- |
|- |
||
| Соотношение || 0.875 || 0.615 |
| Соотношение || 0.875 || colspan="2" | 0.615 |
||
|0.615 |
|||
|} |
|} |
||
{| class="wikitable" |
{| class="wikitable" |
||
|- |
|- |
||
! rowspan="2" | Сумма !! rowspan="2" | Принимавшие |
|||
| ⚫ | |||
лекарство |
|||
| ⚫ | |||
с учетом веса |
|||
|- |
|||
|исходные |
|||
|с весом x22.07 |
|||
|- |
|- |
||
| Выздоровевшие || 850 || 480 |
| Выздоровевшие || 850 || 480 |
||
|2165 |
|||
|4388 |
|||
|- |
|- |
||
| Невыздоровевшие || 870 || 410 |
| Невыздоровевшие || 870 || 410 |
||
|3149 |
|||
|6760.5 |
|||
|- |
|- |
||
| Соотношение || 0.977 || 1.171 |
| Соотношение || 0.977 || 1.171 |
||
|0. |
|0.685 |
||
|} |
|} |
||
Соотношение взвешенного количества выздоровевших к не выздоровевшим среди не принимавших лекарство в этом случае составит 0, |
Соотношение взвешенного количества выздоровевших к не выздоровевшим среди не принимавших лекарство в этом случае составит 0,685, то есть ниже, чем у принимавших лекарство. Это устраняет парадокс и показывает отношение выздоровевших к не выздоровевшим без приема лекарства для такой же пропорции мужчин и женщин, как у принимавших лекарство, что позволяет сравнивать эти цифры. |
||
== См. также == |
== См. также == |
||
* [[Феномен Уилла Роджерса]] |
* [[Феномен Уилла Роджерса]] |
||
* [[Список парадоксов]] |
|||
== Примечания == |
== Примечания == |
||
| Строка 149: | Строка 160: | ||
== Ссылки == |
== Ссылки == |
||
* [http://elementy.ru/news/430970 Использование парадокса Симпсона в модели из живых бактерий] |
* [http://elementy.ru/news/430970 Использование парадокса Симпсона в модели из живых бактерий] — на сайте [http://elementy.ru «Элементы»] |
||
* Секей Г. Парадоксы в теории вероятности и математической статистики |
* Секей Г. Парадоксы в теории вероятности и [[Математическая статистика|математической статистики]] — М.: Мир, 1990. — С. 132—133. — 240 с. |
||
* |
* Judea Pearl. [http://bayes.cs.ucla.edu/R264.pdf Simpson’s Paradox: An Anatomy.] — Technical report — April 1999 — 11 p.{{ref-en}} |
||
* |
* [http://jeff560.tripod.com/s.html Earliest Known Uses of Some of the Words of Mathematics (S)] — Sept. 24, 2011{{ref-en}} |
||
* |
* [http://plato.stanford.edu/entries/paradox-simpson/ Simpson’s Paradox] — First published Mon Feb 2, 2004; substantive revision Thu Aug 6, 2009{{ref-en}} |
||
* |
* [http://www.matifutbol/docs/units/penalty.html And now, who should kick the penalty?]{{Недоступная ссылка|date=Май 2019 |bot=InternetArchiveBot }} — Практический пример парадокса Симпсона на сайте «Matifutbol»{{Недоступная ссылка|date=Май 2019 |bot=InternetArchiveBot }}{{ref-en}} |
||
{{ВС}} |
|||
[[Категория:Вероятностные парадоксы]] |
[[Категория:Вероятностные парадоксы]] |
||
Текущая версия от 09:37, 19 декабря 2024
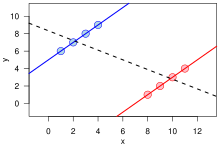
Парадокс Симпсона (также Парадокс Юла — Симпсона или парадокс объединения) — явление в статистике, когда при наличии двух групп данных, в каждой из которых наблюдается одинаково направленная зависимость, при объединении этих групп направление зависимости меняется на противоположное. Например, подсчёты по некоторой группе людей могут говорить, что определённое лекарство увеличивает шанс выздоровления, и при этом если разделить группу на две (мужчин и женщин), то оказывается, что это лекарство уменьшает шанс выздоровления в каждой группе.
Это явление было описано Эдвардом Симпсоном[англ.] в 1951 году и Удни Юлом в 1903 году. Название «парадокс Симпсона» впервые предложил Колин Блайт в 1972 году. Однако, так как Симпсон не был первооткрывателем этого эффекта, некоторые авторы используют безличные названия, например, «парадокс объединения».
История открытия парадокса
[править | править код]Первый раз рассматриваемая ситуация отмечена Карлом Пирсоном в статье «Математический вклад в теорию эволюции»[1]. Он рассматривает зависимость признаков разнородных групп лошадей. Удни Юл делает более подробный анализ подобных популяционных изменений, изучая механизмы наследственности. Симпсон рассматривает то, что он называет «любопытным случаем» в нескольких разделах статьи «The Interpretation of Interaction in Contingency Tables»[2]. Симпсон был первым автором, изучавшим это явление с точки зрения статистики. Поэтому впоследствии математик К. Р. Блайт в статье «On Simpson’s Paradox and the Sure-Thing Principle»[3] вводит термин «парадокс Симпсона».
Примеры
[править | править код]Пример с фишками
[править | править код]Пусть есть четыре шляпы (две чёрных и две серых), 41 фишка (23 цветных и 18 белых) и два стола (А и Б). Фишки распределены по шляпам следующим образом:
- В чёрной шляпе на столе А лежат 5 цветных и 6 белых фишек.
- В серой шляпе на столе А лежат 3 цветные и 4 белые фишки.
- В чёрной шляпе на столе Б лежат 6 цветных и 3 белых фишки.
- В серой шляпе на столе Б лежат 9 цветных и 5 белых фишек.
Допустим, что вы хотите вытащить цветную фишку.
Если вы находитесь около стола А, то вероятность извлечь цветную фишку из чёрной шляпы равна 5/11 = 35/77, а из серой шляпы на том же столе — 3/7 = 33/77; таким образом, цветную фишку больше шансов вытащить из чёрной шляпы, чем из серой.
Если вы находитесь около стола Б, то вероятность извлечь цветную фишку из чёрной шляпы равна 6/9 = 84/126, а из серой шляпы — 9/14 = 81/126; таким образом, и здесь цветную фишку больше шансов вытащить из чёрной шляпы, чем из серой.
Допустим теперь, что фишки из двух чёрных шляп сложены в одну чёрную шляпу, а фишки из двух серых шляп — в одну серую шляпу. На первый взгляд, логично было бы предположить, что вероятность вытащить цветную фишку из чёрной шляпы выше, чем из серой. Но это неверно:
- вероятность вытащить цветную фишку из чёрной шляпы равна 11/20 = 231/420,
- вероятность вытащить цветную фишку из серой шляпы равна 12/21 = 240/420,
то есть больше шансов извлечь цветную фишку из серой шляпы, чем из чёрной[4].
Пример с камнями
[править | править код]Пусть мы имеем четыре набора камней. Вероятность вытащить чёрный камень из набора № 1 выше, чем из набора № 2. В свою очередь, вероятность вытащить чёрный камень из набора № 3 больше, чем из набора № 4. Объединим набор № 1 с набором № 3 (получим набор I), а набор № 2 — с набором № 4 (набор II). Интуитивно можно ожидать, что вероятность вытащить чёрный камень из набора I будет выше, чем из набора II. Однако в общем случае такое утверждение неверно.
Действительно, пусть — число чёрных камней в -ом наборе (выборке), — общее число камней в -ом наборе при . По условию:
Вероятность вытащить чёрный камень из наборов I и II, соответственно:
Выражение для набора I не всегда больше выражения для набора II; то есть может случится, что
Например, при , , , , , , , . Легко проверить, что , , в то время как .
Причины
[править | править код]Причина парадокса заключается в некорректном усреднении двух групп данных с различной долей контрольных наблюдений (нерепрезентативная выборка). Поскольку интуитивно предполагается, что при применении найденных зависимостей доля контрольных будет одинаковой в обеих группах, а в исходных данных это не выполняется, то к ним нельзя применять арифметическое усреднение.
Для устранения проблемы, при усреднении необходимо использовать веса, устраняющие перекос доли контрольных. Так, в примере с фишками доля фишек в серой шляпе на столе А — 7 из 18 (39 %), а на столе Б — 14 из 23 (61 %).
Для репрезентативного усреднения шанса вытянуть цветную фишку достаточно умножить количество фишек обоих цветов в одной из шляп на весовой коэффициент, устраняющий перекос. Например, если вместо одной серой шляпы на столе А поставить две таких же шляпы, то вероятности для каждого стола в отдельности не изменятся, но для объединения столов парадокс будет устранён: вероятность цветной фишки в серой шляпе станет 15/28, то есть меньше, чем из чёрной.
Другой способ разрешения парадокса — использование формулы полной вероятности.
Парадокс Симпсона показывает, что выводы из результатов социологических опросов с нерепрезентативной выборкой нельзя принимать как неопровержимые, доказанные научным путём.
Практическая значимость
[править | править код]Парадокс Симпсона иллюстрирует неправомерность объединений нерепрезентативных выборок без учёта систематического перекоса выборки данных.
Например, в ходе эксперимента в группе мужчин и группе женщин, больных одной и той же болезнью, к стандартному лечению прибавили новый лекарственный препарат. Результат по обеим группам в отдельности подтверждал эффективность нового средства.
| Мужчины | Принимавшие лекарство | Не принимавшие лекарство |
|---|---|---|
| Выздоровевшие | 700 | 80 |
| Невыздоровевшие | 800 | 130 |
| Соотношение | 0.875 | 0.615 |
| Женщины | Принимавшие лекарство | Не принимавшие лекарство |
|---|---|---|
| Выздоровевшие | 150 | 400 |
| Невыздоровевшие | 70 | 280 |
| Соотношение | 2.142 | 1.429 |
Интуитивно предполагается, что если в обеих группах прослеживается зависимость, она должна проявиться и при объединении этих групп. Но хотя соотношение выздоровевших и больных среди и женщин, и мужчин, принимавших лекарство, больше, чем среди тех из них, кто его не использовал, в связи с нерепрезентативностью контрольной группы в агрегированных данных эта закономерность не сохраняется.
| Сумма | Принимавшие лекарство | Не принимавшие лекарство |
|---|---|---|
| Выздоровевшие | 850 | 480 |
| Невыздоровевшие | 870 | 410 |
| Соотношение | 0.977 | 1.171 |
Соотношение в агрегированных данных 850/870<480/410, то есть 0,977<1,171, и доля выздоровевших среди принимавших лекарство оказывается меньше той же доли среди не принимавших.
Для устранения парадокса нужно обратить внимание, что отношение контрольной группы к группе воздействия в приведённых группах резко различается: у мужчин составляет (80+130)/(700+800) = 14%, а у женщин (400+280)/(150+70) = 309%.
Это явно систематическая погрешность, и для корректного усреднения нужно обеспечить репрезентативность контрольной группы в обеих выборках, введя весовые коэффициенты так, чтобы взвешенная доля контрольных в обеих группах стала одинаковой. В данном случае достаточно повысить вес результата тех редких мужчин, кто не принимал лекарства, в 22.07 раза.
Измененные таблицы будут выглядеть так:
| Мужчины | Принимавшие
лекарство |
Не принимавшие лекарство | |
|---|---|---|---|
| исходные | с весом x22.07 | ||
| Выздоровевшие | 700 | 80 | 1765 |
| Невыздоровевшие | 800 | 130 | 2869 |
| Соотношение | 0.875 | 0.615 | |
| Сумма | Принимавшие
лекарство |
Не принимавшие лекарство | |
|---|---|---|---|
| исходные | с весом x22.07 | ||
| Выздоровевшие | 850 | 480 | 2165 |
| Невыздоровевшие | 870 | 410 | 3149 |
| Соотношение | 0.977 | 1.171 | 0.685 |
Соотношение взвешенного количества выздоровевших к не выздоровевшим среди не принимавших лекарство в этом случае составит 0,685, то есть ниже, чем у принимавших лекарство. Это устраняет парадокс и показывает отношение выздоровевших к не выздоровевшим без приема лекарства для такой же пропорции мужчин и женщин, как у принимавших лекарство, что позволяет сравнивать эти цифры.
См. также
[править | править код]Примечания
[править | править код]- ↑ Karl Pearson. Mathematical Contributions to the Theory of Evolution. V. On the Reconstruction of the Stature of Prehistoric Races. Phil. Trans. R. Soc. Lond. A. 1899 192:169-244 doi:10.1098/rsta.1899.0004
- ↑ The Interpretation of Interaction in Contingency Tables // Journal of the Royal Statistical Society, B, 13 (1951) — pp. 238—241
- ↑ Blyth, Colin R. On Simpson’s Paradox and the Sure-Thing Principle // Journal of the American Statistical Association, 67 (1972) — p. 364.
- ↑ М. Гарднер. Глава 19. Индукция и вероятность // Путешествие во времени = Time Travel and Other Mathematical Bewilderments / Перевод с английского Ю. А. Данилова. — М.: Мир, 1990. — С. 278—279. — 341 с. — ISBN 5-03-001166-8.
Ссылки
[править | править код]- Использование парадокса Симпсона в модели из живых бактерий — на сайте «Элементы»
- Секей Г. Парадоксы в теории вероятности и математической статистики — М.: Мир, 1990. — С. 132—133. — 240 с.
- Judea Pearl. Simpson’s Paradox: An Anatomy. — Technical report — April 1999 — 11 p. (англ.)
- Earliest Known Uses of Some of the Words of Mathematics (S) — Sept. 24, 2011 (англ.)
- Simpson’s Paradox — First published Mon Feb 2, 2004; substantive revision Thu Aug 6, 2009 (англ.)
- And now, who should kick the penalty? (недоступная ссылка) — Практический пример парадокса Симпсона на сайте «Matifutbol» (недоступная ссылка) (англ.)

















