Обсуждение:Дельта-функция: различия между версиями
→Неверное утверждение: новая тема |
→δ-Функция как слабый предел: ответ (CD) |
||
| (не показаны 2 промежуточные версии 2 участников) | |||
| Строка 44: | Строка 44: | ||
== Неверное утверждение == |
== Неверное утверждение == |
||
В разделе "δ-Функция как слабый предел". Равенство интеграла от функции f единице недостаточно для того, чтобы nf( |
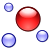
В разделе "δ-Функция как слабый предел". Равенство интеграла от функции <math>f</math> единице недостаточно для того, чтобы <math>nf(nx)</math> сходилось к дельта-функции. В качестве контр-примера достаточно взять функцию <math>-\Big(\frac{\sin x}{x}\Big)'</math> на каком-нибудь отрезке <math>[a,b]</math>, где <math>a < 0</math>, <math>b > 0</math>, так, чтобы интегральное условие сохранялось, а вне отрезка <math>[a,b]</math> положить её равной нулю. Тогда такая <math>nf(nx)</math> будет сходиться к производной δ-функции, а не к самой дельта-функции! Очевидно, в данном разделе неудачно попытались обобщить теорему о δ-образной последовательности, но так нельзя, условие слишком слабо.[[Special:Contributions/85.143.156.231|85.143.156.231]] 10:29, 22 ноября 2017 (UTC)[[Special:Contributions/85.143.156.231|85.143.156.231]] 14:41, 22 ноября 2017 (UTC) |
||
== δ-Функция как слабый предел == |
|||
Вообще-то: |
|||
:<math>\int\limits_{-\infty}^{+\infty}\frac{\sin x}{x}\,dx = \pi</math> |
|||
Но только: |
|||
:<math>\int\limits_{-\infty}^{+\infty}\frac{\sin \pi x}{\pi x}\,dx = 1</math> |
|||
Поэтому в разделе неточность в выборе функции sinc в качестве порождающей для δ-функции. |
|||
[[У:Д.Ильин|Д.Ильин]] ([[ОУ:Д.Ильин|обс.]]) 10:15, 20 апреля 2018 (UTC). |
|||
* Уточнил. [[sinc]] определяется иногда и как sin pi x / pi x. — [[У:Alexei Kopylov|Алексей Копылов]] 21:53, 20 апреля 2018 (UTC) |
|||
Текущая версия от 21:53, 20 апреля 2018
Проект «Математика» (уровень II, важность для проекта высокая)
Эта статья тематически связана с вики-проектом «Математика», цель которого — создание и улучшение статей по темам, связанным с математикой. Вы можете её отредактировать, а также присоединиться к проекту, принять участие в его обсуждении и поработать над требуемыми статьями. |
Проект «Физика» (уровень II, важность для проекта высокая)
Эта статья тематически связана с вики-проектом «Физика», цель которого — создание и улучшение статей по темам, связанным с физикой. Вы можете её отредактировать, а также присоединиться к проекту, принять участие в его обсуждении и поработать над требуемыми статьями. |
Проект «Электроника» (уровень III)
Эта статья тематически связана с вики-проектом «Электроника», цель которого — создание и улучшение статей по темам, связанным с Электроникой. Вы можете её отредактировать, а также присоединиться к проекту, принять участие в его обсуждении и поработать над требуемыми статьями. |
График
[править код]А чё график функции не нарисован? 83.167.116.68 22:55, 28 октября 2009 (UTC)
Замечание
[править код]я считаю, что выше допущены ошибки в вычислениях
именно, не стоит заносить в знаменатель:
- . (2)
потому что для любого
- . (3)
откуда следует, что
- .
здесь можно выполнить предельный переход под знаком интеграла, так как функция интегрируема на бесконечной прямой при любом заданном , поэтому
- . (4)
— Это неподписанное сообщение было добавлено 80.86.249.92 (обс · вклад) 4 декабря
это был я --Kuchumov N 21:58, 6 декабря 2007 (UTC)
Нейтралитет
[править код]«для его понимания не требуется знаний, выходящих за рамки первого курса мехмата МГУ, однако технически громоздко»
По-моему стоит употребить более общий критерий сложности, а не сравнение с какой-то конкретной программой, какого-то конкретного вуза, конкретной страны. Оно звучит как реклама "мы крутые ибо мы учим такие сложные вещи уже на первом курсе". Нейтралитет нужно соблюдать, нейтралитет. FeyFre 08:31, 12 апреля 2011 (UTC)
Неверное утверждение
[править код]В разделе "δ-Функция как слабый предел". Равенство интеграла от функции единице недостаточно для того, чтобы сходилось к дельта-функции. В качестве контр-примера достаточно взять функцию на каком-нибудь отрезке , где , , так, чтобы интегральное условие сохранялось, а вне отрезка положить её равной нулю. Тогда такая будет сходиться к производной δ-функции, а не к самой дельта-функции! Очевидно, в данном разделе неудачно попытались обобщить теорему о δ-образной последовательности, но так нельзя, условие слишком слабо.85.143.156.231 10:29, 22 ноября 2017 (UTC)85.143.156.231 14:41, 22 ноября 2017 (UTC)
δ-Функция как слабый предел
[править код]Вообще-то:
Но только:
Поэтому в разделе неточность в выборе функции sinc в качестве порождающей для δ-функции.
Д.Ильин (обс.) 10:15, 20 апреля 2018 (UTC).
- Уточнил. sinc определяется иногда и как sin pi x / pi x. — Алексей Копылов 21:53, 20 апреля 2018 (UTC)












![{\displaystyle [a,b]}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)



