Гипоциклоида: различия между версиями
| [отпатрулированная версия] | [отпатрулированная версия] |
NapalmBot (обсуждение | вклад) м CheckWiki: исправление синтаксиса тегов. |
Account20 (обсуждение | вклад) →Уравнения: стилевые правки |
||
| (не показано 11 промежуточных версий 7 участников) | |||
| Строка 1: | Строка 1: | ||
[[Файл:HypocycloidK1,66.gif|безрамки|справа]] |
[[Файл:HypocycloidK1,66.gif|безрамки|справа]] |
||
'''Гипоцикло́ида''' ( |
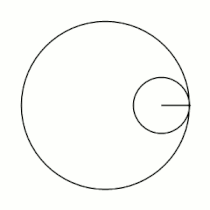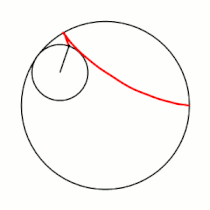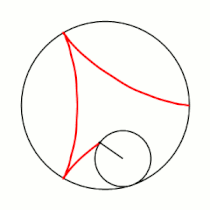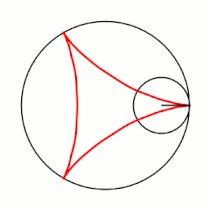
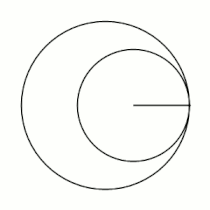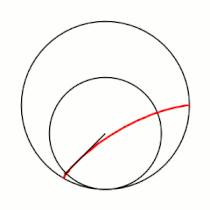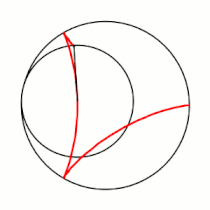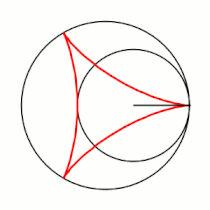
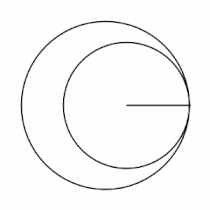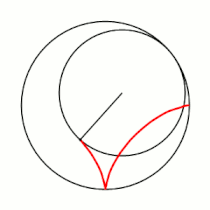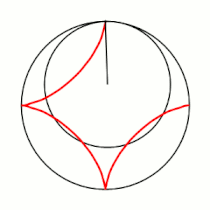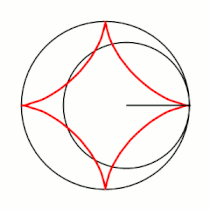
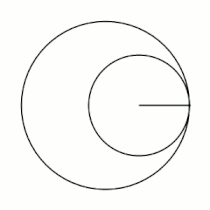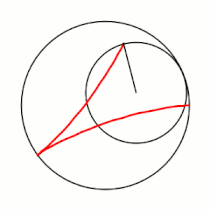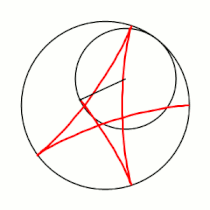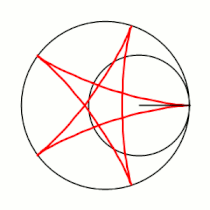
'''Гипоцикло́ида''' ({{lang-el|ὑπό}} (под, внизу) + {{lang-el|κύκλος}} (круг, окружность)) — плоская кривая, образуемая точкой [[окружность|окружности]], катящейся по внутренней стороне другой окружности без скольжения<ref name="БСЭ1">{{ВТ-БСЭ1|Гипоциклоиды и эпициклоиды}}</ref>. |
||
== История == |
|||
[[Файл:Tusi_couple.jpg|мини|Схема гипоциклоиды с k=2 ([[пара Туси]]), сделанная ат-Туси в XIII-м веке<ref>Vatican Library, [https://wps.prenhall.com/esm_chaisson_astronomytoday_5/0,9185,1383966-content,00.html Vat. ar. 319 fol. 28 verso math19 NS.15] {{Webarchive|url=https://web.archive.org/web/20141224122410/https://wps.prenhall.com/esm_chaisson_astronomytoday_5/0,9185,1383966-content,00.html|date=2014-12-24}}, fourteenth-century copy of a manuscript from Tusi</ref>]] |
|||
Впервые частный случай гипоциклодиды, который сейчас известен как [[пара Туси]], был описан [[Исламская астрономия|астрономом]] и [[Математика исламского Средневековья|математиком]] [[Насир ад-Дин ат-Туси|Насир ад-Дином ат-Туси]] в его труде ''Тахрир аль-Маджисти'' в 1247 году<ref>{{Cite web|url=https://mathworld.wolfram.com/|title=Tusi Couple|language=en|first=Eric W.|last=Weisstein|website=mathworld.wolfram.com|access-date=2023-02-27}}</ref><ref>{{Cite book|last=Blake|first=Stephen P.|title=Astronomy and Astrology in the Islamic World|url=https://books.google.com/books?id=3dJVDwAAQBAJ&dq=Tusi+couple+al+majisti&pg=PA67|publisher=Edinburgh University Press|date=2016-04-08|isbn=978-0-7486-4911-2|language=en}}</ref>. Позднее немецкий художник и теоретик [[Возрождение|эпохи Ренессанса]] [[Альбрехт Дюрер]] описал [[Эпитрохоида|эпитрохоиды]] в 1525 году, а [[Рёмер, Оле|Рёмер]] и Бернулли сосредоточились на изучении некоторых специфических гипоциклоид, таких как [[Астроида|астроиды]], в 1674 и 1691 годах соответственно. |
|||
== Уравнения == |
== Уравнения == |
||
[[Файл:Fiery hypocycloid.jpg|thumb| |
[[Файл:Fiery hypocycloid.jpg|thumb|Внутри воздушного шарика катится маленькая батарейка с прикреплённым светодиодом, видна гипоциклоида с k=9|слева]] |
||
[[Параметрическое представление функции|Параметрические уравнения]]: |
[[Параметрическое представление функции|Параметрические уравнения]]: |
||
: <math>\begin{cases}x = r(k-1) \left( \cos t+ \frac{\cos((k-1)t)}{k-1} \right)\\ y = r (k-1) \left( \sin t- \frac{\sin((k-1)t)}{k-1} \right)\end{cases}</math> |
: <math>\begin{cases}x = r(k-1) \left( \cos t+ \frac{\cos((k-1)t)}{k-1} \right)\\ y = r (k-1) \left( \sin t- \frac{\sin((k-1)t)}{k-1} \right)\end{cases}</math> |
||
| Строка 17: | Строка 21: | ||
content-style = text-align: left; | |
content-style = text-align: left; | |
||
content = |
content = |
||
Пусть в начальный момент окружности касаются в точке <math>A</math>, лежащей на оси <math>OX</math>, где точка <math>O</math> |
Пусть в начальный момент окружности касаются в точке <math>A</math>, лежащей на оси <math>OX</math>, где точка <math>O</math> — центр большой окружности. |
||
Координаты точки <math>A</math> при этом - <math>(kr, 0)</math>, где <math>k=\frac{R}{r}</math>. |
|||
Рассмотрим, как меняются координаты точки <math>A</math>, привязанной к катящейся окружности (<math>A</math> переходит в <math>A'</math>). |
|||
Пусть маленькая окружность прокатилась так, что её центр перешел из точки <math>C'</math> в точку <math>C'</math> и повернулся относительно точки <math>O</math> на угол <math>t</math>. Во-первых, можно показать, что поворот маленькой окружности относительно своего центра при этом (т.е. угол между <math>CA</math> и <math>C'A'</math>) равен <math>t - kt = -(k-1)t</math>. Во-вторых, координаты точки <math>C'</math> будут такими: <math>(cos(t)(k-1)r, sin(t)(k-1)r)</math>. Тогда, зная, куда перейдет центр катящейся окружности, и на какой угол она повернулась относительно этого центра, можно записать координаты точки <math>A'</math>: |
Пусть маленькая окружность прокатилась так, что её центр перешел из точки <math>C'</math> в точку <math>C'</math> и повернулся относительно точки <math>O</math> на угол <math>t</math>. Во-первых, можно показать, что поворот маленькой окружности относительно своего центра при этом (т.е. угол между <math>CA</math> и <math>C'A'</math>) равен <math>t - kt = -(k-1)t</math>. Во-вторых, координаты точки <math>C'</math> будут такими: <math>(cos(t)(k-1)r, sin(t)(k-1)r)</math>. Тогда, зная, куда перейдет центр катящейся окружности, и на какой угол она повернулась относительно этого центра, можно записать координаты точки <math>A'</math>: |
||
: <math>\begin{cases} |
: <math>\begin{cases} |
||
| Строка 26: | Строка 32: | ||
|} |
|} |
||
Модуль величины <math>k</math> определяет форму гипоциклоиды. |
Модуль величины <math>k</math> определяет форму гипоциклоиды. |
||
При <math>k=2</math> гипоциклоида описывается [[Пара Туси|парой Туси]] — это [[диаметр]] неподвижной окружности, при <math>k=4</math> является [[астроида|астроидой]]. |
|||
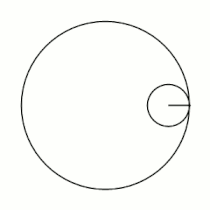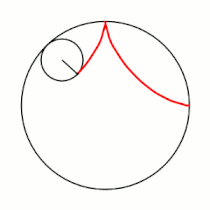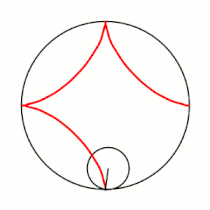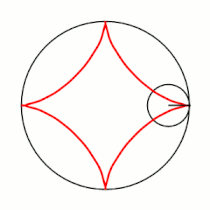
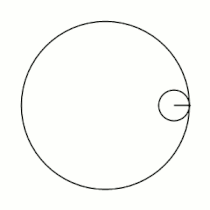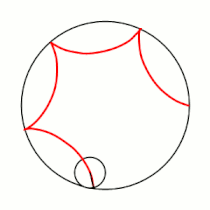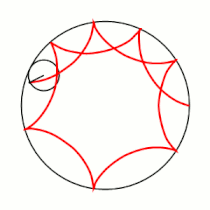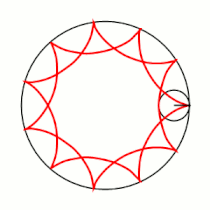
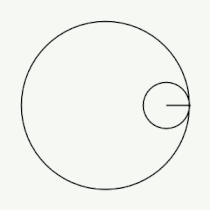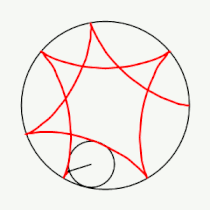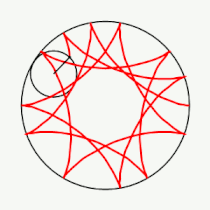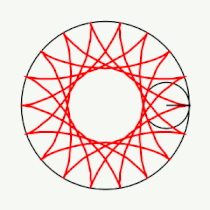
Если модуль <math>k</math> — [[рациональное число|несократимая дробь]] вида <math>\frac{m}{n}</math> (<math>m,n \in \mathbb{N}</math>), то <math>m</math> — это количество [[касп]]ов данной гипоциклоиды, а <math>n</math> — количество полных вращений катящейся окружности. Если модуль <math>k</math> [[иррациональное число]], то кривая является незамкнутой и имеет бесконечное множество несовпадающих каспов. |
Если модуль <math>k</math> — [[рациональное число|несократимая дробь]] вида <math>\frac{m}{n}</math> (<math>m,n \in \mathbb{N}</math>), то <math>m</math> — это количество [[касп]]ов данной гипоциклоиды, а <math>(m-n)</math> — количество полных вращений катящейся окружности. Если модуль <math>k</math> [[иррациональное число]], то кривая является незамкнутой и имеет бесконечное множество несовпадающих каспов. |
||
== Примеры гипоциклоид == |
== Примеры гипоциклоид == |
||
| Строка 55: | Строка 62: | ||
== Литература == |
== Литература == |
||
{{Навигация|Викисловарь = гипоциклоида|Викитека = |}} |
|||
* {{Из КНЭ|2|75|Гипоциклоида}} |
* {{Из КНЭ|2|75|Гипоциклоида}} |
||
{{КНЭ}} |
|||
{{ВС}} |
|||
{{Кривые}} |
{{Кривые}} |
||
Текущая версия от 11:38, 14 сентября 2024

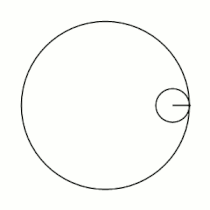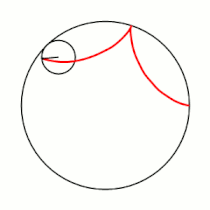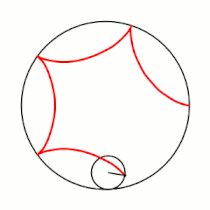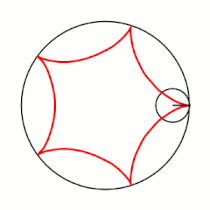
Гипоцикло́ида (греч. ὑπό (под, внизу) + греч. κύκλος (круг, окружность)) — плоская кривая, образуемая точкой окружности, катящейся по внутренней стороне другой окружности без скольжения[1].
История
[править | править код]
Впервые частный случай гипоциклодиды, который сейчас известен как пара Туси, был описан астрономом и математиком Насир ад-Дином ат-Туси в его труде Тахрир аль-Маджисти в 1247 году[3][4]. Позднее немецкий художник и теоретик эпохи Ренессанса Альбрехт Дюрер описал эпитрохоиды в 1525 году, а Рёмер и Бернулли сосредоточились на изучении некоторых специфических гипоциклоид, таких как астроиды, в 1674 и 1691 годах соответственно.
Уравнения
[править | править код]
где , где — радиус неподвижной окружности, — радиус катящейся окружности.
|
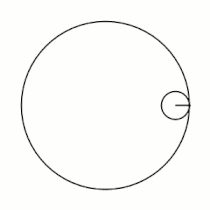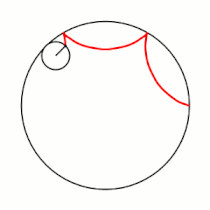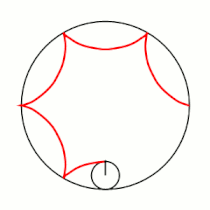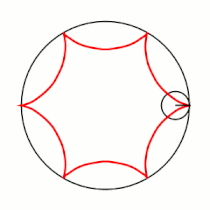
Вывод уравнений Пусть в начальный момент окружности касаются в точке , лежащей на оси , где точка — центр большой окружности. Координаты точки при этом - , где . Рассмотрим, как меняются координаты точки , привязанной к катящейся окружности ( переходит в ). Пусть маленькая окружность прокатилась так, что её центр перешел из точки в точку и повернулся относительно точки на угол . Во-первых, можно показать, что поворот маленькой окружности относительно своего центра при этом (т.е. угол между и ) равен . Во-вторых, координаты точки будут такими: . Тогда, зная, куда перейдет центр катящейся окружности, и на какой угол она повернулась относительно этого центра, можно записать координаты точки : |
Модуль величины определяет форму гипоциклоиды. При гипоциклоида описывается парой Туси — это диаметр неподвижной окружности, при является астроидой. Если модуль — несократимая дробь вида (), то — это количество каспов данной гипоциклоиды, а — количество полных вращений катящейся окружности. Если модуль иррациональное число, то кривая является незамкнутой и имеет бесконечное множество несовпадающих каспов.
Примеры гипоциклоид
[править | править код]
|
См. также
[править | править код]Примечания
[править | править код]- ↑ Гипоциклоиды и эпициклоиды // Большая советская энциклопедия : в 66 т. (65 т. и 1 доп.) / гл. ред. О. Ю. Шмидт. — М. : Советская энциклопедия, 1926—1947.
- ↑ Vatican Library, Vat. ar. 319 fol. 28 verso math19 NS.15 Архивировано 24 декабря 2014 года., fourteenth-century copy of a manuscript from Tusi
- ↑ Weisstein, Eric W. Tusi Couple (англ.). mathworld.wolfram.com. Дата обращения: 27 февраля 2023.
- ↑ Blake, Stephen P. Astronomy and Astrology in the Islamic World : [англ.]. — Edinburgh University Press, 2016-04-08. — ISBN 978-0-7486-4911-2.
Литература
[править | править код]- Гипоциклоида // Казахстан. Национальная энциклопедия. — Алматы: Қазақ энциклопедиясы, 2005. — Т. II. — ISBN 9965-9746-3-2. (CC BY-SA 3.0)