Теорема Мендельсона — Далмейджа: различия между версиями
| [непроверенная версия] | [отпатрулированная версия] |
Bezik (обсуждение | вклад) м Bezik переименовал страницу Теорема Мендельсона-Далмейджа в Теорема Мендельсона — Далмейджа без оставления перенаправления: типографика |
Bezik (обсуждение | вклад) стандартизация (определения для связанных понятий есть в соотв. статьях, утверждение лучше дать сразу в преамбуле, а то получается интрига с раскрытием заголовков в моб. версии) |
||
| Строка 1: | Строка 1: | ||
'''Теорема Мендельсона — Далмейджа''' — утверждение о свойстве [[Паросочетание|паросочетаний]] в [[Двудольный граф|двудольных графах]]: если для двудольного графа <math>G=(X,Y,E)</math> с подмножествами вершин <math>X_1 \sube X</math> и <math>Y_2 \sube Y</math> существуют паросочетания <math>M_1</math> и <math>M_2</math> такие, что <math>M_1</math> насыщает <math>X_1</math>, а <math>M_2</math> насыщает <math>Y_2</math>, то существует паросочетание <math>M</math>, которое насыщает одновременно множества <math>X_1</math> и <math>M_2</math> (Паросочетание <math>M</math> ''насыщает'' подмножество вершин левой (или, соответственно, правой) доли, если для любой вершины в этом подмножестве существует ребро из <math>M</math>, которое [[Глоссарий теории графов# Инцидентность|инцидентно]] этой вершине.) |
|||
| ⚫ | |||
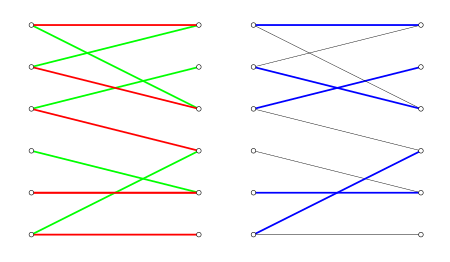
| ⚫ | [[Файл:Mendelsohn-Dulmage-2.svg|мини|450пкс|Паросочетания <math>M_1</math> (красное), <math>M_2</math> (зелёное) и <math>M</math> (синее) из утверждения теоремы. Паросочетание <math>M_1</math> насыщает множество <math>X_1 = \{x_1, x_2, x_3, x_5, x_6\}</math> (вершины на рисунке пронумерованы сверху вниз). Паросочетание <math>M_2</math> насыщает множество <math>Y_2 = \{y_1, y_2, y_3, y_4, y_5\}</math>. Паросочетание <math>M</math> насыщает оба этих множества.]] |
||
| ⚫ | Доказана {{iw|Медельсон, Натан|Натаном Мендельсоном|en|Nathan Mendelsohn}} и [[Далмейдж, Ллойд|Ллойдом Далмейджем]] в [[1958 год в науке|1958 году]]. Следствие из теоремы даёт один из алгоритмов построения оптимальной [[Рёберная раскраска|рёберной раскраски]] двудольного графа (или, что то же самое, разбиения множества рёбер двудольного графа на наименьшее число паросочетаний). |
||
== Определения == |
|||
Граф называется двудольным, если его вершины можно разбить на множества <math>X</math> и <math>Y</math> так, чтобы любое ребро соединяло вершину из множества <math>X</math> с вершиной из множества <math>Y</math>. Такие графы обычно обозначаются <math>G=(X,Y,E)</math>, где <math>E</math> — множество рёбер графа. Множество <math>X</math> называют левой долей графа, а множество <math>Y</math> — правой долей графа. |
|||
[[Паросочетание|Паросочетанием]] в графе называется множество рёбер, не имеющих общих конечных вершин. |
|||
Говорят, что паросочетание <math>M</math> ''насыщает'' подмножество вершин левой (или, соответственно, правой) доли, если для любой вершины в этом подмножестве существует ребро из <math>M</math>, которое [[Глоссарий теории графов# Инцидентность|инцидентно]] этой вершине. |
|||
== Утверждение теоремы == |
|||
[[Файл:Mendelsohn-Dulmage-2.svg|справа|450x450пкс]] |
|||
Пусть <math>G=(X,Y,E)</math> — двудольный граф, в котором обозначены подмножества вершин <math>X_1 \sube X</math> и <math>Y_2 \sube Y</math>. Если существуют паросочетания <math>M_1</math> и <math>M_2</math> такие, что <math>M_1</math> насыщает <math>X_1</math>, а <math>M_2</math> насыщает <math>Y_2</math>, то существует паросочетание <math>M</math>, которое насыщает одновременно множества <math>X_1</math> и <math>M_2</math>. |
|||
== Пример == |
|||
| ⚫ | |||
== Следствия == |
== Следствия == |
||
| ⚫ | В двудольном графе существует паросочетание, насыщающее все вершины максимальной [[Степень вершины (теория графов)|степени]]. Действительно, если максимальная степень вершины в двудольном графе равняется <math>\Delta</math>, то можно взять в качестве множества <math>X_1</math> все вершины левой доли со степенью <math>\Delta</math>, а в качестве множества <math>Y_2</math> — все вершины правой доли со степенью <math>\Delta</math> (одно из множеств <math>X_1</math> и <math>Y_2</math> может быть и пустым); из [[Теорема Холла|теоремы Холла]] следует, что существуют паросочетания <math>M_1</math> и <math>M_2</math>, насыщающие множества <math>X_1</math> и <math>Y_2</math> соответственно. Значит, по теореме Мендельсона — Далмейджа, существует и паросочетание <math>M</math>, насыщающее все вершины степени <math>\Delta</math>. |
||
| ⚫ | Множество рёбер двудольного графа с максимальной степенью вершины <math>\Delta</math> можно разбить на <math>\Delta</math> паросочетаний, или, иными словами, для рёберной раскраски этого графа необходимо и достаточно <math>\Delta</math> цветов (этот результат впервые получен [[Кёниг, Денеш|Кёнигом]]{{sfn|Кёниг|1916}}). Поскольку в графе существует паросочетание, насыщающее все вершины степени <math>\Delta</math>, то удаление из графа всех рёбер этого паросочетания даёт граф с максимальной степенью вершин <math>\Delta - 1</math>; эту процедуру можно повторить до тех пор, пока в графе не останется рёбер. |
||
=== Следствие 1 === |
|||
В двудольном графе существует паросочетание, насыщающее все вершины максимальной [[Степень вершины (теория графов)|степени]]. |
|||
| ⚫ | |||
=== Следствие 2 === |
|||
| ⚫ | Множество рёбер двудольного графа с максимальной степенью вершины <math>\Delta</math> можно разбить на <math>\Delta</math> паросочетаний, или, иными словами, для рёберной раскраски этого графа необходимо и достаточно <math>\Delta</math> цветов (этот результат впервые получен [[Кёниг, Денеш|Кёнигом]]{{sfn|Кёниг|1916}}). |
||
'''Доказательство.''' Рассмотрим все вершины степени <math>\Delta</math>. По следствию 1, в графе существует паросочетание, насыщающее их все. Удалив из графа все рёбра этого паросочетания, получим граф с максимальной степенью вершин <math>\Delta - 1</math>. Повторим для него ту же процедуру, и так далее. В итоге будут построены <math>\Delta</math> паросочетаний, а в графе больше не останется рёбер. |
|||
== Алгоритм и вычислительная сложность == |
== Алгоритм и вычислительная сложность == |
||
| ⚫ | |||
| ⚫ | Алгоритм выполняет <math>\Delta</math> шагов, на каждом нужно построить паросочетания <math>M_1</math> и <math>M_2</math> (это можно сделать [[Алгоритм Хопкрофта — Карпа|алгоритмом Хопкрофта — Карпа]] за время <math>O(|E|\sqrt{|V|})</math>) и паросочетание <math>M</math> (это можно сделать за время <math>O(|E|)</math>). Итоговая сложность работы алгоритма — <math>O(\Delta |E|\sqrt{|V|})</math>. |
||
| ⚫ | |||
== Примечания == |
|||
| ⚫ | Алгоритм выполняет <math>\Delta</math> шагов, на каждом нужно построить паросочетания <math>M_1</math> и <math>M_2</math> (это можно сделать [[Алгоритм Хопкрофта — Карпа|алгоритмом Хопкрофта |
||
== Замечания == |
|||
{{примечания}} |
{{примечания}} |
||
== Ссылки == |
== Ссылки == |
||
| ⚫ | * {{статья|автор= Mendelsohn, N. S., Dulmage, A. L.|заглавие=Some Generalizations of the Problem of Distinct Representatives|издание=Canadian Journal of Mathematics |год=1958|pages=230—241|volume=10|ссылка=https://www.cambridge.org/core/journals/canadian-journal-of-mathematics/article/some-generalizations-of-the-problem-of-distinct-representatives/D1EBF9514B99A740AF8C74FFEE7C4758}} |
||
| ⚫ | * {{статья|автор= Mendelsohn, N. S., Dulmage, A. L.|заглавие=Some Generalizations of the Problem of Distinct Representatives|издание=Canadian Journal of Mathematics |год=1958|pages= |
||
* {{книга |
* {{книга |
||
| автор = Свами М., Тхуласираман К. |
| автор = Свами М., Тхуласираман К. |
||
| Строка 51: | Строка 26: | ||
| ref= Свами, Тхуласираман |
| ref= Свами, Тхуласираман |
||
}} |
}} |
||
* {{статья |
* {{статья |
||
| автор = Kőnig, D |
| автор = Kőnig, D |
||
Версия от 23:32, 26 сентября 2022
Теорема Мендельсона — Далмейджа — утверждение о свойстве паросочетаний в двудольных графах: если для двудольного графа с подмножествами вершин и существуют паросочетания и такие, что насыщает , а насыщает , то существует паросочетание , которое насыщает одновременно множества и (Паросочетание насыщает подмножество вершин левой (или, соответственно, правой) доли, если для любой вершины в этом подмножестве существует ребро из , которое инцидентно этой вершине.)
Доказана Натаном Мендельсоном[англ.] и Ллойдом Далмейджем в 1958 году. Следствие из теоремы даёт один из алгоритмов построения оптимальной рёберной раскраски двудольного графа (или, что то же самое, разбиения множества рёбер двудольного графа на наименьшее число паросочетаний).
Следствия
В двудольном графе существует паросочетание, насыщающее все вершины максимальной степени. Действительно, если максимальная степень вершины в двудольном графе равняется , то можно взять в качестве множества все вершины левой доли со степенью , а в качестве множества — все вершины правой доли со степенью (одно из множеств и может быть и пустым); из теоремы Холла следует, что существуют паросочетания и , насыщающие множества и соответственно. Значит, по теореме Мендельсона — Далмейджа, существует и паросочетание , насыщающее все вершины степени .
Множество рёбер двудольного графа с максимальной степенью вершины можно разбить на паросочетаний, или, иными словами, для рёберной раскраски этого графа необходимо и достаточно цветов (этот результат впервые получен Кёнигом[1]). Поскольку в графе существует паросочетание, насыщающее все вершины степени , то удаление из графа всех рёбер этого паросочетания даёт граф с максимальной степенью вершин ; эту процедуру можно повторить до тех пор, пока в графе не останется рёбер.
Алгоритм и вычислительная сложность
Доказательство теоремы Мендельсона — Далмейджа и следствий из неё фактически является алгоритмом разбиения рёбер двудольного графа на наименьшее число паросочетаний.
Алгоритм выполняет шагов, на каждом нужно построить паросочетания и (это можно сделать алгоритмом Хопкрофта — Карпа за время ) и паросочетание (это можно сделать за время ). Итоговая сложность работы алгоритма — .
Примечания
Ссылки
- Mendelsohn, N. S., Dulmage, A. L. Some Generalizations of the Problem of Distinct Representatives // Canadian Journal of Mathematics. — 1958. — Vol. 10. — P. 230—241.
- Свами М., Тхуласираман К. Графы, сети и алгоритмы. — М.: Мир, 1984. — 455 с. — ISBN 978-5-458-33391-7.
- Kőnig, D. Uber Graphen und ihre Anwendung auf Determinantentheorie und Mengenlehre // Mathematische Annalen. — 1916. — Т. 77, вып. 4. — С. 453—465. — doi:10.1007/BF01456961.
На эту статью не ссылаются другие статьи Википедии. |














