Геостационарная орбита: различия между версиями
| [непроверенная версия] | [отпатрулированная версия] |
Alic (обсуждение | вклад) м Правильно будет "орбита захоронения" + ссылка |
м Разрешение значений с помощью бота: Ньютон - Changed link(s) to Ньютон, Исаак; косметические изменения |
||
| Строка 1: | Строка 1: | ||
[[ |
[[Файл:Geostat.gif|thumb|250px|Геостационарная орбита]] |
||
'''Геостациона́рная орби́та''' (ГСО) — круговая [[орбита]], расположенная над [[экватор]]ом [[Земля (планета)|Земли]] (0° широты), находясь на которой, искусственный [[Искусственный спутник Земли|спутник]] обращается вокруг планеты с [[Угловая скорость|угловой скоростью]], равной угловой скорости вращения Земли вокруг оси, и постоянно находится над одной и той же точкой на земной поверхности. Геостационарная орбита является разновидностью [[геосинхронная орбита|геосинхронной орбиты]] и используется для размещения искусственных спутников (коммуникационных, телетрансляционных и т. п.) |
'''Геостациона́рная орби́та''' (ГСО) — круговая [[орбита]], расположенная над [[экватор]]ом [[Земля (планета)|Земли]] (0° широты), находясь на которой, искусственный [[Искусственный спутник Земли|спутник]] обращается вокруг планеты с [[Угловая скорость|угловой скоростью]], равной угловой скорости вращения Земли вокруг оси, и постоянно находится над одной и той же точкой на земной поверхности. Геостационарная орбита является разновидностью [[геосинхронная орбита|геосинхронной орбиты]] и используется для размещения искусственных спутников (коммуникационных, телетрансляционных и т. п.) |
||
| Строка 14: | Строка 14: | ||
== [[Список геостационарных спутников|Размещение спутников на орбите]] == |
== [[Список геостационарных спутников|Размещение спутников на орбите]] == |
||
[[Изображение:Пояс Кларка для Архангельска.jpg|300px|thumb|Для Архангельска максимально возможная высота спутника над горизонтом — 17,2°<br/> |
[[Изображение:Пояс Кларка для Архангельска.jpg|300px|thumb|Для Архангельска максимально возможная высота спутника над горизонтом — 17,2°<br /> |
||
Наивысшая точка [[Пояс Кларка|пояса Кларка]] всегда находится строго на юге. |
Наивысшая точка [[Пояс Кларка|пояса Кларка]] всегда находится строго на юге. |
||
В нижней части графика градусы — меридианы, над которыми находятся спутники.<br/> |
В нижней части графика градусы — меридианы, над которыми находятся спутники.<br /> |
||
По бокам — высоты спутников над горизонтом.<br/> |
По бокам — высоты спутников над горизонтом.<br /> |
||
Сверху — направление на спутник. |
Сверху — направление на спутник. |
||
| Строка 36: | Строка 36: | ||
где <math>F_{u}</math> — сила инерции, а в данном случае, центробежная сила; <math>F_{\Gamma}</math> — гравитационная сила. |
где <math>F_{u}</math> — сила инерции, а в данном случае, центробежная сила; <math>F_{\Gamma}</math> — гравитационная сила. |
||
Величину гравитационной силы, действующую на спутник, можно определить по закону всемирного тяготения [[Ньютон]] |
Величину гравитационной силы, действующую на спутник, можно определить по закону всемирного тяготения [[Ньютон, Исаак|Ньютона]]: |
||
<center><math>F_{\Gamma} = G \cdot \frac{M_3 \cdot m_c}{R^2}</math>,</center> |
<center><math>F_{\Gamma} = G \cdot \frac{M_3 \cdot m_c}{R^2}</math>,</center> |
||
| Строка 96: | Строка 96: | ||
== См. также == |
== См. также == |
||
*[[Синхронная орбита]] |
* [[Синхронная орбита]] |
||
*[[Геосинхронная орбита]] |
* [[Геосинхронная орбита]] |
||
*[[Солнечно-синхронная орбита]] |
* [[Солнечно-синхронная орбита]] |
||
*[[Низкая опорная орбита]] |
* [[Низкая опорная орбита]] |
||
*[[Геопереходная орбита]] |
* [[Геопереходная орбита]] |
||
*[[Космический лифт]] |
* [[Космический лифт]] |
||
== Ссылки == |
== Ссылки == |
||
Версия от 06:12, 10 ноября 2009
Геостациона́рная орби́та (ГСО) — круговая орбита, расположенная над экватором Земли (0° широты), находясь на которой, искусственный спутник обращается вокруг планеты с угловой скоростью, равной угловой скорости вращения Земли вокруг оси, и постоянно находится над одной и той же точкой на земной поверхности. Геостационарная орбита является разновидностью геосинхронной орбиты и используется для размещения искусственных спутников (коммуникационных, телетрансляционных и т. п.)
Идея использования геостационарных спутников для целей связи высказывалась ещё К. Э. Циолковским и словенским теоретиком космонавтики Германом Поточником. Преимущества геостационарной орбиты получили широкую известность после выхода в свет научно-популярной статьи Артура С. Кларка в журнале «Wireless World» в 1945 году, поэтому на Западе геостационарная и геосинхронные орбиты иногда называются «орбитами Кларка». Первым спутником, успешно выведенным на ГСО был Syncom-2, запущенный NASA в июле 1963 года.
Спутник должен обращаться в направлении вращения Земли, на высоте 35 786 км над уровнем моря (вычисление высоты ГСО см. ниже). Именно такая высота обеспечивает спутнику период обращения, равный периоду вращения Земли (сидерические сутки: 23 часа, 56 минут, 4,091 секунды).
Точка стояния
Спутник, находящийся на геостационарной орбите, кажется неподвижным из любой точки на поверхности Земли. В результате, неподвижно закреплённая направленная антенна может сохранять постоянную связь с этим спутником.
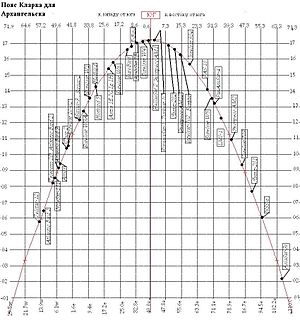
Наивысшая точка пояса Кларка всегда находится строго на юге. В нижней части графика градусы — меридианы, над которыми находятся спутники.
По бокам — высоты спутников над горизонтом.
Сверху — направление на спутник. Для наглядности можно растянуть по горизонтали в 7,8 раза и отразить слева направо. Тогда он будет выглядеть так же, как на небе.
Геостационарная орбита может быть точно обеспечена только на окружности, расположенной прямо над экватором, с высотой, очень близкой к 35 786 км.
Для перевода спутников с низковысотной орбиты на геостационарную используются переходные геостационарные (геопереходные) орбиты (ГПО) — эллиптические орбиты с перигеем на низкой высоте и апогеем на высоте, близкой к геостационарной орбите.
После завершения активной эксплуатации на остатках топлива спутник должен быть переведён на орбиту захоронения, расположенную на 200-300 км выше ГСО.
Вычисление параметров геостационарной орбиты
Радиус орбиты и высота орбиты
На геостационарной орбите спутник не приближается к Земле и не удаляется от неё, и кроме того, вращаясь вместе с Землёй, постоянно находится над какой-либо точкой на экваторе. Следовательно, действующие на спутник силы гравитации и центробежная сила должны уравновешивать друг друга. Для вычисления высоты геостационарной орбиты можно воспользоваться методами классической механики и исходить из следующего уравнения:
где — сила инерции, а в данном случае, центробежная сила; — гравитационная сила. Величину гравитационной силы, действующую на спутник, можно определить по закону всемирного тяготения Ньютона:
где — масса спутника, — масса Земли в килограммах, — гравитационная постоянная, а — расстояние в метрах от спутника до центра Земли или, в данном случае, радиус орбиты.
Величина центробежной силы равна:
где — центростремительное ускорение, возникающее при круговом движении по орбите.
Как можно видеть, масса спутника присутствует как множитель в выражениях для центробежной силы и для гравитационной силы, то есть высота орбиты не зависит от массы спутника, что справедливо для любых орбит[1] и является следствием равенства гравитационной и инертной массы. Следовательно, геостационарная орбита определяется лишь высотой, при которых центробежная сила будет равна по модулю и противоположна по направлению гравитационной силе, создаваемой притяжением Земли на данной высоте.
Центростремительное ускорение равно:
где — угловая скорость вращения спутника, в радианах в секунду.
Уравнивая выражения для гравитационной силы и центробежной силы с подстановкой центростремительного ускорения, получаем:
Сокращая , переводя влево, а вправо, получаем:
или
Можно записать это выражение иначе, заменив на — геоцентрическую гравитационную постоянную:
Угловая скорость вычисляется делением угла, пройденного за один оборот ( радиан) на период обращения (время, за которое совершается один полный оборот по орбите: один сидерический день, или 86 164 секунды). Получаем:
Полученный радиус орбиты составляет 42 164 км. Вычитая экваториальный радиус Земли, 6 378 км, получаем высоту 35 786 км.
Орбитальная скорость
Орбитальная скорость (скорость, с которой спутник летит в космосе), вычисляется умножением угловой скорости на радиус орбиты:
Длина орбиты
Длина геостационарной орбиты: . При радиусе орбиты 42 164 км получаем длину орбиты 264 924 км.
Длина орбиты крайне важна для вычисления "точек стояния" спутников.
Связь
Связь через такого рода спутники характеризуется большими задержками в распространении сигнала. Даже один ход луча до спутника и обратно обходится почти в четверть секунды. Ping до другой точки на земле будет уже около половины секунды.
При высоте орбиты 35 786 км и скорости света около 300 000 км/с ход луча "Земля-спутник" требует 35786/300000 =~0,12 сек. Ход луча "Земля (передатчик) -> спутник -> Земля (приемник)" ~0,24 сек. Ping потребует ~0,48 сек
С учетом задержки сигнала в аппаратуре ИСЗ и аппаратуре наземных служб общая задержка сигнала на маршруте Земля -> спутник -> Земля может достигать 2-4 с. [1]
См. также
- Синхронная орбита
- Геосинхронная орбита
- Солнечно-синхронная орбита
- Низкая опорная орбита
- Геопереходная орбита
- Космический лифт
Ссылки
- «Основы геостационарной орбиты» Д-р Т.С. Келсо
- «ДВИЖЕНИЕ СПУТНИКОВ» на сайте «Физика в анимациях»
- Статья Леонида Невдяева
Примечания
- ↑ для орбит спутников, масса которых пренебрежимо мала по сравнению с массой притягивающего его астрономического объекта
















![{\displaystyle R={\sqrt[{3}]{\frac {G\cdot M_{3}}{\omega ^{2}}}}}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/02a60d2974a63b5d47597cbf38e088ff3909d4bd)


![{\displaystyle R={\sqrt[{3}]{\frac {\mu }{\omega ^{2}}}}}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/d2984d9fa34b8b17fabeceff9bc75a78011a0594)




