Гипоциклоида

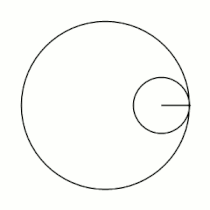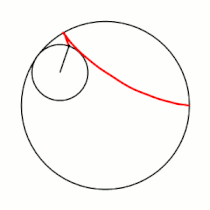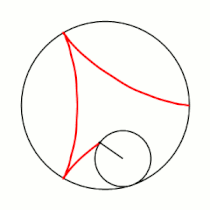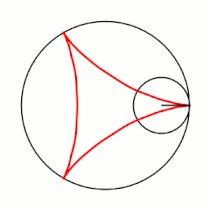
Гипоцикло́ида (от греческих слов ὑπό — под, внизу и κύκλος — круг, окружность) — плоская кривая, образуемая точкой окружности, катящейся по внутренней стороне другой окружности без скольжения.

Уравнения

Внутри воздушного шарика катится маленькая батарейка с прикреплённым светодиодом, видна гипоциклоида с k=9

Параметрические уравнения:

${\begin{cases}x=r(k-1)\left(\cos t+{\frac {\cos((k-1)t)}{k-1}}\right)\\y=r(k-1)\left(\sin t-{\frac {\sin((k-1)t)}{k-1}}\right)\end{cases}}$

где $\textstyle k={\frac {R}{r}}$, где $R$ — радиус неподвижной окружности, $r$ — радиус катящейся окружности.

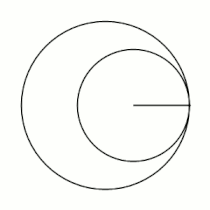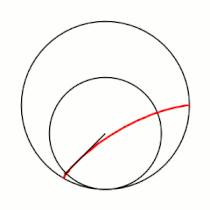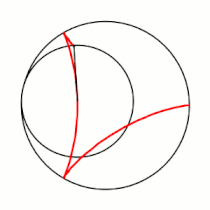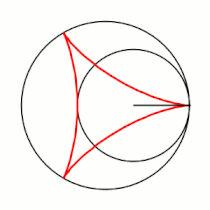
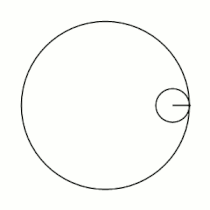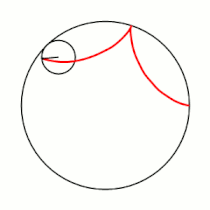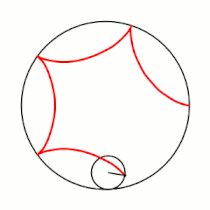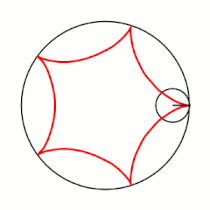
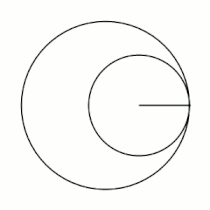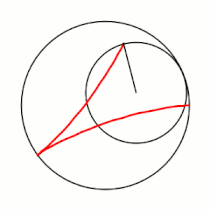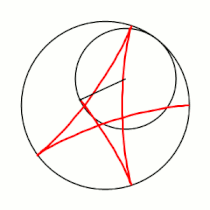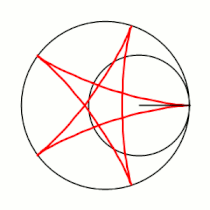
Вывод уравнений Пусть в начальный момент окружности касаются в точке $A$, лежащей на оси $OX$, где точка $O$ — центр большой окружности. Координаты точки $A$ при этом - $(kr,0)$, где $k={\frac {R}{r}}$. Рассмотрим, как меняются координаты точки $A$, привязанной к катящейся окружности ($A$ переходит в $A'$). Пусть маленькая окружность прокатилась так, что её центр перешел из точки $C'$ в точку $C'$ и повернулся относительно точки $O$ на угол $t$. Во-первых, можно показать, что поворот маленькой окружности относительно своего центра при этом (т.е. угол между $CA$ и $C'A'$) равен $t-kt=-(k-1)t$. Во-вторых, координаты точки $C'$ будут такими: $(cos(t)(k-1)r,sin(t)(k-1)r)$. Тогда, зная, куда перейдет центр катящейся окружности, и на какой угол она повернулась относительно этого центра, можно записать координаты точки $A'$: ${\begin{cases}x=cos(t)(k-1)r+cos((k-1)t)r\\y=sin(t)(k-1)r-sin((k-1)t)r\end{cases}}$

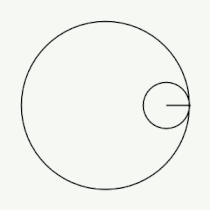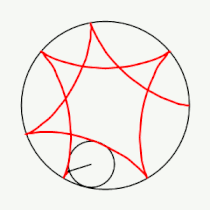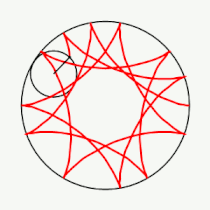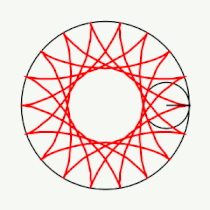
Модуль величины $k$ определяет форму гипоциклоиды. При $k=2$ гипоциклоида описывается парой Туси — это диаметр неподвижной окружности, при $k=4$ является астроидой. Если модуль $k$ — несократимая дробь вида ${\frac {m}{n}}$ ($m,n\in \mathbb {N}$), то $m$ — это количество каспов данной гипоциклоиды, а $(m-n)$ — количество полных вращений катящейся окружности. Если модуль $k$ иррациональное число, то кривая является незамкнутой и имеет бесконечное множество несовпадающих каспов.

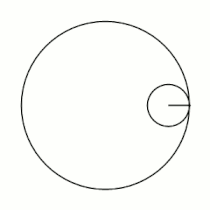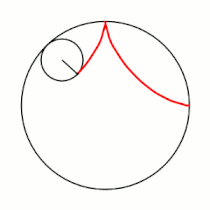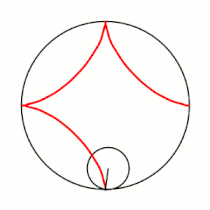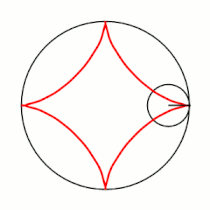
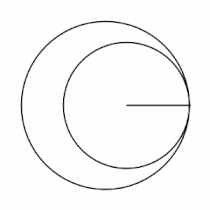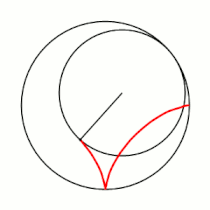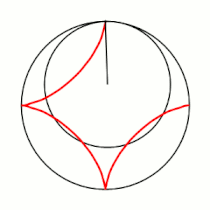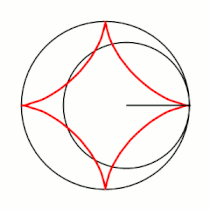
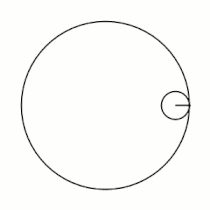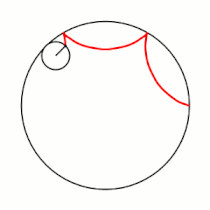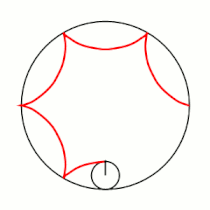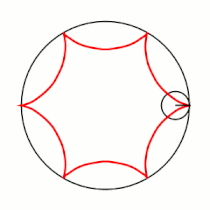
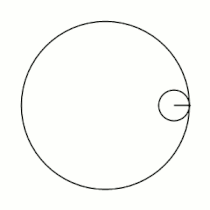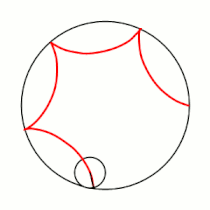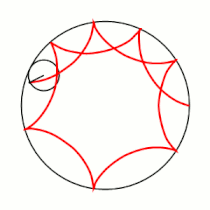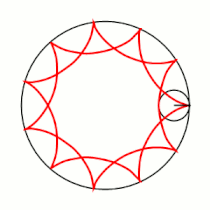
Примеры гипоциклоид

$k=3$ — Дельтоида $k=1.5={\frac {3}{2}}$ $k=4$ — Астроида $k={\frac {4}{3}}$ $k=5$ $k=6$ $k=5.5={\frac {11}{2}}$ $k={\frac {5}{3}}$ $k=3.6={\frac {18}{5}}$

См. также

• Циклоида
• Эпициклоида
• Гипотрохоида

Литература

• Гипоциклоида // Казахстан. Национальная энциклопедия (рус.). — Алматы: Қазақ энциклопедиясы, 2005. — Т. II. — ISBN 9965-9746-3-2. (CC BY-SA 3.0)

При написании этой статьи использовался материал из издания «Казахстан. Национальная энциклопедия» (1998—2007), предоставленного редакцией «Қазақ энциклопедиясы» по лицензии Creative Commons BY-SA 3.0 Unported.