Теорема Менелая

Теоре́ма Менела́я или теорема о трансверсалях или теорема о полном четырёхстороннике — классическая теорема аффинной геометрии.

Формулировка

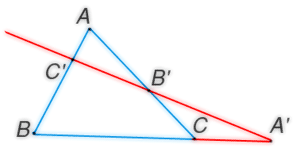
Если точки $A',B'$ и $C'$ лежат соответственно на сторонах $BC,CA$ и $AB$ треугольника $\triangle ABC$ или на их продолжениях, то они коллинеарны тогда и только тогда, когда

${\frac {AB'}{B'C}}\cdot {\frac {CA'}{A'B}}\cdot {\frac {BC'}{C'A}}=1.$

где ${\frac {AB'}{B'C}}$, ${\frac {CA'}{A'B}}$ и ${\frac {BC'}{C'A}}$ обозначают отношения направленных отрезков.

Доказательство

Проведем через точку $C$ прямую, параллельную прямой $AB$, и обозначим через $K$ точку пересечения этой прямой с прямой $A'C'$. Поскольку треугольники $\triangle AC'B'$ и $\triangle CKB'$ подобны (по двум углам), то

${\frac {|AC'|}{|CK|}}={\frac {|B'A|}{|B'C|}}$.

Так как подобными являются также треугольники $\triangle BC'A'$ и $\triangle CKA'$, тем самым

${\frac {|CK|}{|C'B|}}={\frac {|A'C|}{|BA'|}}$.

Исключая $CK$, получаем

${\frac {|AC'|}{|C'B|}}\cdot {\frac {|BA'|}{|A'C|}}\cdot {\frac {|CB'|}{|B'A|}}=1$.

Остаётся заметить, что возможны два расположения точек $A',B'$ и $C'$: либо две из них лежат на соответствующих сторонах треугольника, а третья — на продолжении, либо все три лежат на продолжениях соответствующих сторон. Отсюда для отношений направленных отрезков имеем

${\frac {AB'}{B'C}}\cdot {\frac {CA'}{A'B}}\cdot {\frac {BC'}{C'A}}=-1.$

Замечания

• В частности, из теоремы следует соотношение для длин отрезков:

  ${\frac {|AB'|}{|B'C|}}\cdot {\frac {|CA'|}{|A'B|}}\cdot {\frac {|BC'|}{|C'A|}}=1.$

Вариации и обобщения

• Тригонометрический эквивалент:

${\frac {\sin \angle BAA'}{\sin \angle A'AC}}\cdot {\frac {\sin \angle CBB'}{\sin \angle B'BA}}\cdot {\frac {\sin \angle ACC'}{\sin \angle C'CB}}=-1$, где все углы — ориентированные.

• В сферической геометрии теорема Менелая приобретает вид

${\frac {\sin |AB'|}{\sin |B'C|}}\cdot {\frac {\sin |CA'|}{\sin |A'B|}}\cdot {\frac {\sin |BC'|}{\sin |C'A|}}=1.$

• В геометрии Лобачевского теорема Менелая приобретает вид

${\frac {\operatorname {sh} |AB'|}{\operatorname {sh} |B'C|}}\cdot {\frac {\operatorname {sh} |CA'|}{\operatorname {sh} |A'B|}}\cdot {\frac {\operatorname {sh} |BC'|}{\operatorname {sh} |C'A|}}=1.$

История

Эта теорема доказывается в третьей книге «Сферики» Менелая Александрийского (около 100 года нашей эры). Менелай сначала доказывает теорему для плоского случая, а потом центральным проектированием переносит её на сферу. Возможно, что плоский случай теоремы рассматривался ранее в несохранившихся «Поризмах» Евклида.

Сферическая теорема Менелая была основным средством, с помощью которого решались разнообразные прикладные задачи позднеантичной и средневековой астрономии и геодезии. Ей посвящён ряд сочинений под названием «Книга о фигуре секущих», составленных такими математиками средневекового Востока, как Сабит ибн Корра, ан-Насави, ал-Магриби, ас-Сиджизи, ас-Салар, Джабир ибн Афлах, Насир ад-Дин ат-Туси.

Итальянский математик Джованни Чева в 1678 году предложил доказательство теоремы Менелая и родственной ей теоремы Чевы для плоского случая, основанное на рассмотрении центра тяжести системы из трёх точечных грузов.

Применения

• Теорема Сальмона
• Многие теоремы проективной геометрии, например Теорема Паппа и Теорема Дезарга доказываются многократным применением теоремы Менелая.

См. также

• Прямая Гаусса
• Теорема Чевы
• Теорема Ван-Обеля о треугольнике

Ссылки

• Ефремов Д. Новая геометрия треугольника. — Одесса, 1902. — 334 с.
• Коксетер Г. С. М., Грейтцер С. П. Новые встречи с геометрией. — М.: Наука, 1978. — Т. 14. — (Библиотека математического кружка).
• Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 73-74. — ISBN 5-94057-170-0.
• Шаль, Мишель. О теореме Птоломея относительно треугольника, пересечённого трансверсалью // Исторический обзор происхождения и развития геометрических методов. — М., 1883. — Т. 2.
• Sidoli N. The sector theorem attributed to Menelaus // SCIAMVS. — 2006. — № 7. — С. 43–79.