Двухщелевой опыт: различия между версиями
| [непроверенная версия] | [непроверенная версия] |
Xeonz (обсуждение | вклад) отмена правки 104571135 участника 31.134.130.24 (обс.) вандализм Метка: отмена |
поставлено ударение Метки: с мобильного устройства из мобильной версии через расширенный мобильный режим |
||
| Строка 1: | Строка 1: | ||
[[Файл:Double-slit.svg|мини| Фотоны или частицы вещества (например, электрон) создают волновую картину, когда используются две щели ]] |
[[Файл:Double-slit.svg|мини| Фотоны или частицы вещества (например, электрон) создают волновую картину, когда используются две щели ]] |
||
''' |
'''Двухщелево́й опыт''' в {{Не переведено 3|Современная физика|современной физике|4=Modern physics}} является демонстрацией того, что свет и материя в целом могут проявлять характеристики как классических волн, так и частиц; кроме того, он отображает фундаментально вероятностный характер [[Квантовая механика|квантово-механических]] явлений. Впервые опыт был проведен [[Юнг, Томас|Томасом Юнгом]] со светом в 1801 году. В 1927 году [[Опыт Дэвиссона — Джермера|Дэвиссон и Гермер]] продемонстрировали, что электроны проявляют такое же поведение, которое позднее расширено на атомы и молекулы.<ref name="medium.com">«[https://medium.com/the-physics-arxiv-blog/462c39db8e7b Physicists Smash Record For Wave-Particle Duality]»</ref><ref name="Eibenberger 2013 pp. 14696–14700">{{статья |заглавие=Matter-wave interference with particles selected from a molecular library with masses exceeding 10000 amu |издание={{Нп3|Physical Chemistry Chemical Physics}} |том=15 |номер=35 |страницы=14696—14700 |doi=10.1039/C3CP51500A |arxiv=1310.8343 |bibcode=2013PCCP...1514696E |pmid=23900710 |язык=en |тип=journal |автор=Sandra; Eibenberger et al. |год=2013}}</ref> |
||
[[Опыт Юнга|Опыт Томаса Юнга]] со светом<ref>While there is no doubt that Young’s demonstration of optical interference, using sunlight, pinholes and cards, played a vital part in the acceptance of the wave theory of light, there is some question as to whether he ever actually performed a double-slit interference experiment. |
[[Опыт Юнга|Опыт Томаса Юнга]] со светом<ref>While there is no doubt that Young’s demonstration of optical interference, using sunlight, pinholes and cards, played a vital part in the acceptance of the wave theory of light, there is some question as to whether he ever actually performed a double-slit interference experiment. |
||
Версия от 22:06, 8 апреля 2020

Двухщелево́й опыт в современной физике[англ.] является демонстрацией того, что свет и материя в целом могут проявлять характеристики как классических волн, так и частиц; кроме того, он отображает фундаментально вероятностный характер квантово-механических явлений. Впервые опыт был проведен Томасом Юнгом со светом в 1801 году. В 1927 году Дэвиссон и Гермер продемонстрировали, что электроны проявляют такое же поведение, которое позднее расширено на атомы и молекулы.[1][2]
Опыт Томаса Юнга со светом[3] был частью классической физики задолго до квантовой механики и концепции корпускулярно-волнового дуализма. Он полагал, что это продемонстрировало правильность волновой теории света. Его опыт иногда называют «щели Юнга».
Этот опыт относится к общему классу опытов с «двойным путем», в которых первоначальная волна разделяется на две раздельные, которые впоследствии снова объединяются в одну. Изменения длины пути обеих волн приводят к сдвигу фаз, создавая интерференционную картину . Другой версией опыта является интерферометр Маха-Цендера, который разделяет луч при помощи зеркала.
В базовой версии этого опыта источник когерентного света, такой как лазерный луч, освещает пластину с двумя параллельными щелями, и свет, проходящий через щели, наблюдают на экране за пластиной.[4][5] Волновая природа света вызывает интерференцию световых волн, проходящих через две щели, создавая яркие и темные полосы на экране — результат, которого не должно было бы быть, если бы свет состоял из классических частиц.[4][6] Однако всегда обнаруживается, что свет поглощается на экране в отдельных точках, в виде отдельных частиц (не волн), а интерференционная картина появляется из-за изменяющейся плотности попадания этих частиц на экран.[7] Кроме того, версии опыта, включающие детекторы в щелях, обнаруживают, что каждый обнаруженный фотон проходит только через одну щель (как классическая частица), а не через обе щели (как волна).[8][9][10][11][12] Тем не менее, такие опыты показывают, что частицы не образуют интерференционную картину, если наблюдать, через какую щель они проходят. Эти результаты демонстрируют принцип корпускулярно-волнового дуализма.[13][14]
Обнаружено, что другие объекты атомного масштаба, например электроны, проявляют то же поведение при стрельбе по двойной щели.[5] Кроме того, наблюдение отдельных дискретных взаимодействий по своей природе является вероятностным, что необъяснимо с помощью классической механики.[5]
Опыт может быть сделан с намного более крупными объектами, чем электроны и фотоны, хотя он становится более сложным с увеличением размеров. Крупнейшими объектами, для которых был проведен опыт с двумя щелями, были молекулы, каждая из которых содержала 810 атомов (общая масса которых составляла более 10000 атомных единиц массы).[1][2]
Двухщелевой опыт (и его вариации) стал классическим мысленным экспериментом, как яркий пример загадок квантовой механики. Поскольку он демонстрирует фундаментальное ограничение способности наблюдателя прогнозировать экспериментальные результаты, Ричард Фейнман назвал это «явлением, которое невозможно […] объяснить каким-либо классическим способом, и в котором заложено сердце квантовой механики. В действительности, оно содержит единственную тайну [квантовой механики].»[5]
Обзор

Если бы свет состоял строго из обычных или классических частиц, и эти частицы выпускались бы по прямой линии через щель, что позволяло бы им попадать в экран на другой стороне, мы ожидали бы увидеть изображение, соответствующее размеру и форме щели. Однако, когда этот "эксперимент с одной щелью" выполняется в реальности, изображение на экране представляет собой дифракционную картину распределения света. Чем меньше щель, тем больше угол расхождения. В верхней части изображения показана центральная часть паттерна, сформированного при освещении лазером щели. Также можно заметить две слабые боковые полосы. Большее число полос можно увидеть с более точной установкой. Изображение объясняется дифракцией как результат интерференции световых волн от щели.
Если освещать две параллельные щели, то свет от двух щелей дополнительно интерферирует. Здесь интерференция представляет собой более выраженный паттерн с чередованием светлых и темных полос. Ширина полос зависит от частоты испускаемого света.[15] (См. нижнюю фотографию справа.) Когда Томас Янг (1773–1829) впервые продемонстрировал это явление, он указал, что свет состоит из волн, поскольку распределение яркости может быть объяснено попеременно аддитивной и вычитающей интерференцией волнового фронта.[5] Опыт Юнга, выполненный в начале 1800-х годов, сыграл критически важную роль в принятии волновой теории света, победив корпускулярную теорию света?!, предложенную Исааком Ньютоном, которая была принятой моделью распространения света в 17-м и 18-м веках. Однако позднее обнаружение фотоэлектрического эффекта продемонстрировало, что при различных обстоятельствах свет может вести себя так, как если бы он состоял из дискретных частиц. Эти, казалось бы, противоречивые открытия заставили выйти за рамки классической физики и принять во внимание квантовую природу света.
Фейнман любил говорить, что всю квантовую механику можно получить из тщательного обдумывания последствий этого единственного эксперимента.[16] Он также предложил (в качестве мысленного эксперимента), что размещение детекторов перед каждой щелью приведет к исчезнованию интерференционной картины.[17]
Соотношение дуализма Энглерта–Гринбергера[англ.] подробно описывает математику двухщелевой интерференции в контексте квантовой механики.
Низкоинтенсивный двухщелевой опыт был впервые выполнен Г. И. Тейлором в 1909г.[18] путем снижения уровня падающего света до тех пор, пока события испускания/поглощения фотонов большей частью не перекрывались. Двухщелевой опыт не проводился ни с чем, кроме света, до 1961 года, когда Клаус Йонссон из Тюбингенского университета выполнил его с электронными пучками.[19][20] В 1974 году итальянские физики Пьер Джорджо Мерли, Джан Франко Миссироли и Джулио Поцци повторили опыт, используя одиночные электроны и бипризму (вместо щелей), показав, что каждый электрон взаимодействует с самим собой, как и предсказывает квантовая теория.[21][22] В 2002 году одноэлектронная версия опыта была признана читателями журнала Physics World "самым красивым экспериментом".[23]
В 2012 году Стефано Фраббони и его коллеги в конечном итоге провели двухщелевой опыт с электронами и реальными щелями, следуя оригинальной схеме, предложенной Фейнманом. Они посылали одиночные электроны на нанофабрикатные щели (шириной около 100 нм) и, собирая прошедшие электроны одноэлектронным детектором, смогли показать накопление двухщелевой интерференционной картины.[24]
В 2019 году Марко Джаммарки и его коллеги продемонстрировали интерференцию отдельных частиц для антиматерии.[25]
Варианты опыта
Интерференция отдельных частиц

Важная версия этого эксперимента подразумевает одиночные частицы (или волны - для согласованности они называются здесь частицами). Испускание одиночных частиц через устройство с двумя щелями приводит к ожидаемому появлению на экране одиночных частиц. Примечательно, однако, что интерференционная картина возникает, если эти частицы накапливать (см. соседнее изображение). Это демонстрирует корпускулярно-волновой дуализм, который утверждает, что вся материя проявляет свойства как волн, так и частиц: частица измеряется как один импульс в одной позиции, а волна описывает вероятность поглощения частицы в определенном месте на экране.[26] Было показано, что это явление происходит с фотонами, электронами, атомами и даже некоторыми молекулами, включая букибол.[27][28][29][30][31] Таким образом, эксперименты с электронами добавляют подтверждающее доказательство к мнению, что электроны, протоны, нейтроны и даже более крупные объекты, которые обычно называют частицами, тем не менее, имеют свою собственную волновую природу и даже длину волны (связанную с их импульсом).
Вероятность обнаружения является квадратом амплитуды волны и может быть рассчитана с помощью классических волн (см. ниже ). Частицы не попадают на экран в определенном порядке, поэтому знание того, где появились на экране и в каком порядке все предыдущие частицы, ничего не говорит о том, где будет обнаружена следующая частица.[32] Если в какой-то месте происходит затухание волн, это не означает исчезновение частицы; она появится где-то в другом месте. С момента появления квантовой механики некоторые теоретики искали способы включения дополнительных детерминант или "скрытых параметров", зная которые было бы возможно определять местоположение каждого отдельного попадания в мишень. [33]
Более сложные системы, которые включают две и более частиц в суперпозиции, приведенному выше объяснению не поддаются.[34]
Опыты по выявлению пути и принцип дополнительности
Известный мысленный эксперимент предсказывает, что если детекторы частиц будут расположены на щелях, показывая, через какую щель проходит фотон, интерференционная картина исчезнет.[5] Этот опыт по выявлению пути иллюстрирует принцип дополнительности, согласно которому фотоны могут вести себя как частицы или волны, но не могут одновременно наблюдаться в обоих вариантах.[35][36][37] Несмотря на важность этого мысленного эксперимента в истории квантовой механики (например, см. обсуждение версии этого эксперимента Эйнштейном ), технически осуществимые реализации этого эксперимента не существовали до 1970-х годов.[38] (Наивные реализации эксперимента Геданкена из учебника невозможны, поскольку фотоны не могут быть обнаружены без его поглощения.) В настоящее время было проведено несколько экспериментов, иллюстрирующих различные аспекты дополнимости. [39]
Эксперимент, проведенный в 1987 году[40][41] дал результаты, которые продемонстрировали, что можно получить информацию о том, по какому пути прошла частица, вообще не разрушая интерференцию. Это продемонстрировало эффект измерения, которое слабо воздействовало на летящие частицы и тем самым сопоставимо влияло на интерференционную картину. Другими словами, если не настаивать на полностью надежном методе, используемом для определения щели, через которую проходит каждый фотон, по прежнему наблюдается (ухудшенная) интерференционная картина.[42]
Отложенный выбор и варианты квантового ластика
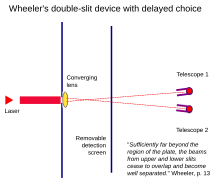
Эксперименты Уилера с отложенным выбором[англ.]* демонстрируют, что извлечение информации о пути после того, как частица прошла через щели, может, как кажется, задним числом поменять предшествующее поведение на щелях.
Эксперименты с квантовым ластиком демонстрируют, что волновое поведение может быть восстановлено путем стирания информации о пути.
Простая "домашняя" иллюстрация "квантового ластика" была дана в статье в журнале Scientific American.[43] Если установить поляризаторы перед каждой щелью так, чтобы их оси были ортогональны друг другу, интерференционная картина пропадет. Поляризаторы могут рассматриваться как добавляющие к каждому лучу информацию о пути. Введение третьего поляризатора перед детектором с осью 45° относительно других поляризаторов, "стирает" эту информацию, восстанавливая интерференционную картину. Это также можно объяснить, рассматривая свет как классическую волну[43]:91 а также при использовании круговых поляризаторов и одиночных фотонов.[44]:6 Реализации поляризаторов с использованием запутанных фотонных пар не имеют классического объяснения.[44]
Слабое измерение
В широко разрекламированном эксперименте 2012 года исследователи утверждали, что определили путь, по которому прошла каждая частица, без какого-либо отрицательного воздействия на интерференционную картину.[45] Для этого они использовали установку, где частицы вылетали не из точечного источника, а из источника с двумя максимумами интенсивности. Однако такие комментаторы, как Свенссон [46], отметили, что на самом деле нет никакого конфликта между слабыми измерениями, выполненными в этом варианте двухщелевого эксперимента, и принципом неопределенности Гейзенберга . Слабое измерение с последующим выбором не позволяло одновременно измерять положение и импульс для каждой отдельной частицы, а скорее позволяло измерять среднюю траекторию частиц, которые попали в разные позиции. Другими словами, экспериментаторы создавали статистическую карту ландшафта полной траектории.
Другие варианты


В 1967 году Пфлегор и Мандель продемонстрировали интерференцию с двумя источниками, используя два отдельных лазера в качестве источников света.[47][48]
В 1972 году экспериментально было показано, что в двухщелевой системе, в которой была открыта только одна щель, тем не менее наблюдалась интерферения при условии разности путей, позволяющей детектируемому фотону приходить из любой щели.[49][50] Плотность фотонов в экспериментальной системе была значительно меньше единицы.
В 1999 году эксперимент с двумя щелями был успешно проведен с молекулами букибола (каждая из которых содержит 60 атомов углерода).[28][51] Букибол достаточно большой (диаметр около 0,7нм, почти в полмиллиона раз больше, чем протон), что позволяет наблюдать его под электронным микроскопом .
В 2005 году Э.Р. Элиель представил экспериментальное и теоретическое исследование оптического пропускания тонкого металлического экрана, с двумя щелями размерами менее длины волны, разделенными расстоянием, превышающим длину волны во много раз. Показано, что общая интенсивность паттерна двойной щели в дальней зоне уменьшается или увеличивается как функция длины волны падающего светового пучка.[52]
В 2012 году исследователи из Университета штата Небраска-Линкольн выполнили двухщелевой эксперимент с электронами, как описано Ричардом Фейнманом, с использованием новых инструментов, которые позволили контролировать проход двух щелей и отслеживать события обнаружения единичных электронов. Электроны запускались электронной пушкой и проходили через одну или две щели 62нм шириной и 4мкм высотой.[53]
В 2013 году двухщелевой опыт был успешно проведен с молекулами, каждая из которых содержала 810 атомов (общая масса которых превышала 10000 атомных единиц массы ).[1][2]
Гидродинамические аналоги пилот-волны
Были разработаны гидродинамические аналоги[англ.], которые могут воссоздать различные аспекты квантово-механических систем, включая одночастичную интерференцию через двойную щель.[54] Капля силиконового масла, отскакивая вдоль поверхности жидкости, самостоятельно движется посредством резонансных взаимодействий с собственным волновым полем. Капля мягко выплескивает жидкость при каждом скачке. В то же время на ее ход влияет рябь от прошлых отскоков. Взаимодействие капли с ее собственной рябью, которая образует так называемую пилот-волну, приводит к тому, что капля демонстрирует поведение, ранее считавшееся характерным для элементарных частиц, - в том числе поведение, обычно принимаемое в качестве доказательства того, что элементарные частицы распространяются в пространстве, как волны, без какого-либо конкретное местоположения, до измерения.[55][56]
Поведения, имитируемые с помощью такой гидродинамической системы пилот-волн, включают в себя квантовую одночастичную дифракцию,[57] туннелирование, квантованные орбиты, расщепление орбитальных уровней, спин и мультимодальную статистику. Также можно вывести соотношение неопределенностей и принципы запрета. Имеются видеоролики, иллюстрирующие различные свойства такой системы. (См. Внешние ссылки.)
Тем не менее, более сложные системы, которые включают суперпозицию двух и более частиц, не поддаются такому простому, классически интуитивному объяснению.[34] Соответственно, не существует гидродинамического аналога квантовой запутанности. [54] Тем не менее, возможны оптические аналоги. [58]
Классическая волновая оптика



Большая часть поведения света может быть смоделирована с использованием классической волновой теории. Принцип Гюйгенса–Френеля является одной из таких моделей; в нем говорится, что каждая точка волнового фронта генерирует вторичную волну, и что возмущение в любой последующей точке можно найти, суммируя вклады отдельных волн в этой точке. Это суммирование должно учитывать фазу и амплитуду отдельных волн. Измерена может быть только интенсивность светового поля, которая пропорционально квадрату амплитуды.
В двухщелевом опыте обе щели освещаются одним лазерным лучом. Если ширина щелей достаточно мала (меньше длины волны лазерного излучения), щели рассеивают свет на цилиндрические волны. Эти два цилиндрических волновых фронта накладываются друг на друга, и амплитуда и, следовательно, интенсивность в любой точке комбинированных волновых фронтов зависят как от величины, так и от фазы двух волновых фронтов. Разница в фазе между двумя волнами определяется разницей в расстоянии, пройденном этими волнами.
Если расстояние наблюдения велико по сравнению с разнесением щелей (дальнее поле[англ.]), разность фаз можно найти с помощью геометрии, показанной на нижнем правом рисунке. Разница в пути между двумя волнами, проходящими под углом θ, определяется как:
Где d - расстояние между двумя щелями. Когда две волны находятся в фазе, то есть разность путей равна целому числу длин волн, суммарная амплитуда и, следовательно, суммарная интенсивность максимальны, а когда они находятся в противофазе, то есть разность путей равна половине длина волны, полторы длины волны и т. д., то волны вычитаются и суммарная интенсивность равна нулю. Этот эффект известен как интерференция . Максимумы интерференционных полос возникают под углами
где λ - длина волны света. Угловое расстояние между полосами, θf задаются как
Расстояние между полосами на расстоянии z от щелей определяется как
Например, если две щели разделены на 0,5 мм (d) и освещены лазером с длиной волны 0,6мкм (λ), то на расстоянии 1м (z) расстояние между полосами составит 1,2 мм.
Если ширина щелей b больше длины волны, уравнение дифракции Фраунгофера дает интенсивность дифрагированного света как:[59]
Где функция sinc определяется как sinc(x) = sin(x)/x для x ≠ 0 и sinc(0) = 1.
Это показано на рисунке выше, где первый паттерн представляет собой дифракционную картину от одной щели, заданную функцией sinc в этом уравнении, а второй рисунок показывает суммарную интенсивность света, дифрагированного от двух щелей, где функция cos формирует тонкую структуру, а более грубая структура формирует дифракцию от отдельных щелей, согласно функции sinc.
Аналогичные вычисления для ближнего поля[англ.] могут быть выполнены с использованием уравнения дифракции Френеля. По мере того, как плоскость наблюдения становится ближе к плоскости щелей, связанные с каждой щелью дифракционные картины уменьшаются в размерах, так что площадь интерференции уменьшается и может вообще исчезнуть, если нет перекрытия двух дифракционных картин.[60]
Интерпретации эксперимента
Как и мысленный эксперимент кота Шредингера, двухщелевой опыт часто используется для демонстрации различий и сходств между разными интерпретациями квантовой механики .
Копенгагенская интерпретация
Копенгагенская интерпретация, выдвинутая некоторыми пионерами в области квантовой механики, утверждает, что нежелательно постулировать что-либо, выходящее за рамки математических формул, физической аппаратуры и результатов, которые позволяют нам получить некоторые знания о том, что происходит на атомном уровне. Одну из математических конструкций, которая позволяет экспериментаторам очень точно прогнозировать определенные экспериментальные результаты, иногда называют "волна вероятности". По своей математической форме она аналогичен описанию физической волны, но ее "гребни" и "впадины" указывают уровни вероятности возникновения определенных явлений (например, вспышки света в определенной точке на экране детектора), которые можно наблюдать в макромире повседневного опыта.
Можно сказать, что "волна" вероятности "проходит через пространство", потому что значения вероятности, которые можно вычислить из ее математического представления, зависят от времени. Нельзя говорить о местонахождении какой-либо частицы, такой как фотон, между моментами испускания и обнаружения, просто потому, что для утверждения о нахождении объекта в определенном месте в определенное время, нужно его обнаружить (детектировать). Требование возможного появления интерференционной картины состоит в том, что должны быть испускаемые частицы и экран с, по меньшей мере, двумя различными путями, по которым частица должна пройти от излучателя к экрану. В экспериментах нету наблюдения в промежуток времени между испусканием частицы и ее попаданием в экран. Если произвести трассировка лучей так, как будто световая волна (как понимается в классической физике) достаточно широка для прохождения обоих путей, то эта трассировка будет точно предсказывать появление максимумов и минимумов на экране детектора, когда многие частицы проходят через аппарат и постепенно "раскрашивают" ожидаемую интерференционную картину.
Формулировка через интегралы по траекториям

Копенгагенская интерпретация аналогична формулировке квантовой механики через интегралы по траекториям, предложенной Фейнманом. Формула интеграла по траекториям заменяет классическое понятие единственной уникальной траектории для системы суммой по всем возможным траекториям. Траектории складываются вместе с помощью функционального интеграла .
Каждый путь считается одинаково вероятным и, следовательно, вносит одинаковый вклад. Однако фаза этого вклада в любой заданной точке пути определяется действием на пути:
Все эти вклады затем складываются, и величина конечного результата возводится в квадрат, чтобы получить распределение вероятностей для положения частицы:
Как всегда при расчете вероятности, результаты должны быть нормализованы[англ.] путем наложения:
Подводя итог, можно сказать, что распределение вероятностей исхода - это нормализованный квадрат нормы суперпозиции по всем путям от точки происхождения до конечной точки волн, распространяющихся[англ.] пропорционально действию вдоль каждого пути. Различия в кумулятивном действии вдоль различных путей (и, следовательно, относительных фаз вкладов) создают интерференционную картину, наблюдаемую в двухщелевом опыте. Фейнман подчеркнул, что его формулировка является просто математическим описанием, а не попыткой описать реальный измеряемый процесс.
Реляционная интерпретация

Согласно реляционной интерпретации квантовой механики, впервые предложенной Карло Ровелли,[61] наблюдения, подобные наблюдениям в двухщелевом опыте, являются результатом взаимодействия наблюдателя[англ.] (измерительного устройства) и наблюдаемого объекта (с которым физически взаимодействуют), а не какого-либо абсолютного свойства объекта. В случае электрона, если он изначально "наблюдается" на определенной щели, то взаимодействие наблюдатель-частица (фотон-электрон) включает информацию о положении электрона. Это частично ограничивает конечное местоположение частицы на экране. Если он "наблюдается" (измеряется с помощью фотона) не на конкретной щели, а на экране, то информация о пути не является частью взаимодействия, поэтому "наблюдаемое" положение электрона на экране определяется строго его вероятностной функции. Это делает результирующее изображение на экране таким же, как если бы каждый отдельный электрон прошел через обе щели. Также было высказано предположение, что пространство и расстояние сами по себе являются реляционными, и что электрон может оказаться в "двух местах одновременно" - например, на обеих щелях - потому что его пространственные отношения с конкретными точками на экране остаются идентичными с положений щелей.[62]
Многомировая интерпретация
Физик Дэвид Дойч утверждает в своей книге Структура реальности, что двухщелевой эксперимент является доказательством многомировой интерпретации. Однако, поскольку любая интерпретация квантовой механики эмпирически неразличима, некоторые ученые скептически относятся к этому утверждению.
Теория де Бройля – Бома
Альтернатива общепринятому пониманию квантовой механики, теория де Бройля-Бома утверждает, что частицы всегда имеют точное местоположение и что их скорости зависят от волновой функции. Таким образом, в то время как отдельная частица пройдет через одну конкретную щель в двухщелевом опыте, так называемая "пилотная волна", которая влияет на нее, пройдет через обе. Траектории двойной щели де Бройля-Бома были впервые рассчитаны Крисом Дьюдни во время работы с Крисом Филиппидисом и Бэзилом Хили в Биркбек-колледже (Лондон).[63] Теория де Бройля-Бома дает те же статистические результаты, что и стандартная квантовая механика, но обходится без многих ее концептуальных трудностей. [64]
См. также
Ссылки
- ↑ 1 2 3 «Physicists Smash Record For Wave-Particle Duality»
- ↑ 1 2 3 Sandra; Eibenberger et al. Matter-wave interference with particles selected from a molecular library with masses exceeding 10000 amu (англ.) // Physical Chemistry Chemical Physics[англ.] : journal. — 2013. — Vol. 15, no. 35. — P. 14696—14700. — doi:10.1039/C3CP51500A. — . — arXiv:1310.8343. — PMID 23900710.
- ↑ While there is no doubt that Young’s demonstration of optical interference, using sunlight, pinholes and cards, played a vital part in the acceptance of the wave theory of light, there is some question as to whether he ever actually performed a double-slit interference experiment.
- ↑ 1 2 Lederman, Leon M.; Christopher T. Hill. Quantum Physics for Poets (неопр.). — US: Prometheus Books[англ.], 2011. — С. 102—111. — ISBN 978-1616142810.
- ↑ 1 2 3 4 5 6 Feynman, Richard P.; Robert B. Leighton; Matthew Sands. The Feynman Lectures on Physics, Vol. 3 (неопр.). — Addison-Wesley, 1965. — С. 1.1—1.8. — ISBN 978-0201021189.
- ↑ Feynman, 1965, p. 1.5
- ↑ Darling. Wave–Particle Duality. The Internet Encyclopedia of Science. The Worlds of David Darling. Дата обращения: 18 октября 2008.
- ↑ Feynman, 1965, p. 1.7
- ↑ Leon Lederman; Christopher T. Hill. Quantum Physics for Poets (неопр.). — Prometheus Books, Publishers, 2011. — С. 109. — ISBN 978-1-61614-281-0.
- ↑ «…if in a double-slit experiment, the detectors which register outcoming photons are placed immediately behind the diaphragm with two slits: A photon is registered in one detector, not in both…» Müller-Kirsten, H. J. W. Introduction to Quantum Mechanics: Schrödinger Equation and Path Integral (англ.). — US: World Scientific, 2006. — P. 14. — ISBN 978-981-2566911.
- ↑ Plotnitsky, Arkady. Niels Bohr and Complementarity: An Introduction (англ.). — US: Springer[англ.], 2012. — P. 75—76. — ISBN 978-1461445173.
- ↑ «It seems that light passes through one slit or the other in the form of photons if we set up an experiment to detect which slit the photon passes, but passes through both slits in the form of a wave if we perform an interference experiment.» Rae, Alastair I.M. Quantum Physics: Illusion Or Reality? (неопр.). — UK: Cambridge University Press, 2004. — С. 9—10. — ISBN 978-1139455275.
- ↑ Feynman, The Feynman Lectures on Physics, 3:Quantum Mechanics p.1-1 «There is one lucky break, however— electrons behave just like light.».
- ↑ See: Davisson-Germer experiment C. J; Davisson. The diffraction of electrons by a crystal of nickel (англ.) // Bell System Technical Journal[англ.] : journal. — 1928. — Vol. 7. — P. 90—105. — doi:10.1002/j.1538-7305.1928.tb00342.x.
- ↑ Charles Sanders Peirce first proposed the use of this effect as an artifact-independent reference standard for length
- ↑ Greene, Brian. The Elegant Universe: Super Strings, Hidden Dimensions, and the Quest for the Ultimate Theory (англ.). — New York: W.W. Norton?!, 1999. — P. 97—109. — ISBN 978-0-393-04688-5.
- ↑ Feynman, 1965, chapter 3
- ↑ Ingram Taylor[англ.]. Interference Fringes with Feeble Light (неопр.) // Prof. Cam. Phil. Soc.. — 1909. — Т. 15.
- ↑ Claus; Jönsson. Elektroneninterferenzen an mehreren künstlich hergestellten Feinspalten (нем.) // Zeitschrift für Physik : magazin. — 1961. — 1 August (Bd. 161, Nr. 4). — S. 454—474. — ISSN 0044-3328. — doi:10.1007/BF01342460. — .
- ↑ Claus; Jönsson. Electron Diffraction at Multiple Slits (англ.) // American Journal of Physics?! : journal. — 1974. — 1 January (vol. 42, no. 1). — P. 4—11. — ISSN 0002-9505. — doi:10.1119/1.1987592. — .
- ↑ P G; Merli. On the statistical aspect of electron interference phenomena (англ.) // American Journal of Physics?! : journal. — 1976. — Vol. 44, no. 3. — P. 306—307. — doi:10.1119/1.10184. — .
- ↑ R; Rosa. The Merli–Missiroli–Pozzi Two-Slit Electron-Interference Experiment (англ.) // Physics in Perspective[англ.] : journal. — 2012. — Vol. 14, no. 2. — P. 178—194. — doi:10.1007/s00016-011-0079-0. — . — PMID 26525832.
- ↑ "The most beautiful experiment". Physics World 2002.
- ↑ Stefano; Frabboni. The Young-Feynman two-slits experiment with single electrons: Build-up of the interference pattern and arrival-time distribution using a fast-readout pixel detector (англ.) // Ultramicroscopy[англ.] : journal. — 2012. — May (vol. 116). — P. 73—76. — ISSN 0304-3991. — doi:10.1016/j.ultramic.2012.03.017.
- ↑ Science Advances 03 May 2019: Vol. 5, no. 5, eaav7610 DOI: 10.1126/sciadv.aav7610
- ↑ Greene, Brian. The Fabric of the Cosmos: Space, Time, and the Texture of Reality (англ.). — Random House LLC?!, 2007. — P. 90. — ISBN 978-0-307-42853-0.
- ↑ O; Donati. An Experiment on Electron Interference (англ.) // American Journal of Physics?! : journal. — 1973. — Vol. 41, no. 5. — P. 639—644. — doi:10.1119/1.1987321. — .
- ↑ 1 2 New Scientist: Quantum wonders: Corpuscles and buckyballs, 2010 (Introduction, subscription needed for full text, quoted in full in Архивировано 25 сентября 2017 года.)
- ↑ Wave Particle Duality of C60 Архивировано 31 марта 2012 года.
- ↑ Olaf; lNairz. Diffraction of Complex Molecules by Structures Made of Light (англ.) // Phys. Rev. Lett. : journal. — 2001. — Vol. 87, no. 16. — doi:10.1103/physrevlett.87.160401. — . — arXiv:quant-ph/0110012. — PMID 11690188.
- ↑ O; Nairz. Quantum interference experiments with large molecules (англ.) // American Journal of Physics?! : journal. — 2003. — Vol. 71, no. 4. — P. 319—325. — doi:10.1119/1.1531580. — . Архивировано 8 августа 2017 года.
- ↑ Brian Greene, The Elegant Universe, p. 104, pp. 109–114
- ↑ Greene, Brian. The Fabric of the Cosmos: Space, Time, and the Texture of Reality (англ.). — Knopf[англ.], 2004. — P. 204—213. — ISBN 978-0-375-41288-2.
- ↑ 1 2 Baggott, Jim (2011). The Quantum Story: A History in 40 Moments. New York: Oxford University Press. pp. 76. ("The wavefunction of a system containing N particles depends on 3N position coordinates and is a function in a 3N-dimensional configuration space or 'phase space'. It is difficult to visualize a reality comprising imaginary functions in an abstract, multi-dimensional space. No difficulty arises, however, if the imaginary functions are not to be given a real interpretation.")
- ↑ Harrison. Complementarity and the Copenhagen Interpretation of Quantum Mechanics. UPSCALE. Dept. of Physics, U. of Toronto. Дата обращения: 21 июня 2008.
- ↑ Cassidy. Quantum Mechanics 1925–1927: Triumph of the Copenhagen Interpretation. Werner Heisenberg. American Institute of Physics.
- ↑ Boscá Díaz-Pintado, María C. (29-31 March 2007). "Updating the wave-particle duality". 15th UK and European Meeting on the Foundations of Physics. Leeds, UK. Дата обращения: 21 июня 2008.
{{cite conference}}: Неизвестный параметр|booktitle=игнорируется (|book-title=предлагается) (справка)Википедия:Обслуживание CS1 (формат даты) (ссылка) - ↑ L.; Bartell. Complementarity in the double-slit experiment: On simple realizable systems for observing intermediate particle-wave behavior (англ.) // Physical Review D : journal. — 1980. — Vol. 21, no. 6. — P. 1698—1699. — doi:10.1103/PhysRevD.21.1698. — .
- ↑ A.; Zeilinger. Experiment and the foundations of quantum physics (англ.) // Reviews of Modern Physics : journal. — 1999. — Vol. 71, no. 2. — P. S288—S297. — doi:10.1103/RevModPhys.71.S288. — .
- ↑ P. Mittelstaedt. Unsharp particle-wave duality in a photon split-beam experiment (англ.) // Foundations of Physics[англ.] : journal. — 1987. — Vol. 17, no. 9. — P. 891—903. — doi:10.1007/BF00734319. — .
- ↑ D.M. Greenberger and A. Yasin, "Simultaneous wave and particle knowledge in a neutron interferometer", Physics Letters A 128, 391–4 (1988).
- ↑ W. K.; Wootters. Complementarity in the double-slit experiment: Quantum nonseparability and a quantitative statement of Bohr's principle (англ.) // Phys. Rev. D : journal. — 1979. — Vol. 19, no. 2. — P. 473—484. — doi:10.1103/PhysRevD.19.473. — .
- ↑ 1 2 Hillmer, R.; Kwiat, P. A do-it-yourself quantum eraser (англ.) // Scientific American : magazine. — Springer Nature, 2007. — Vol. 296, no. 5. — P. 90—95. — doi:10.1038/scientificamerican0507-90. — .
- ↑ 1 2 Chiao, R. Y.; P. G. Kwiat; Steinberg, A. M. Quantum non-locality in two-photon experiments at Berkeley (англ.) // Quantum and Semiclassical Optics: Journal of the European Optical Society Part B : journal. — 1995. — Vol. 7, no. 3. — P. 259—278. — doi:10.1088/1355-5111/7/3/006. — . — arXiv:quant-ph/9501016.
- ↑ Francis. Disentangling the wave-particle duality in the double-slit experiment. Ars Technica (21 мая 2012).
- ↑ Bengt E. Y.; Svensson. Pedagogical Review of Quantum Measurement Theory with an Emphasis on Weak Measurements (англ.) // Quanta : journal. — 2013. — Vol. 2, no. 1. — P. 18—49. — doi:10.12743/quanta.v2i1.12. — arXiv:1202.5148.
- ↑ Pfleegor, R. L. Interference of Independent Photon Beams (англ.) // Physical Review : journal. — 1967. — July (vol. 159, no. 5). — P. 1084—1088. — doi:10.1103/PhysRev.159.1084. — .
- ↑ Interference of Independent Photon Beams: The Pfleegor-Mandel Experiment. Дата обращения: 16 июня 2011. Архивировано 3 января 2011 года.>
- ↑ Sillitto, R.M. An interference experiment with light beams modulated in anti-phase by an electro-optic shutter (англ.) // Physics Letters A[англ.] : journal. — 1972. — Vol. 39, no. 4. — P. 333—334. — doi:10.1016/0375-9601(72)91015-8. — .
- ↑ "To a light particle"
- ↑ Markus; Arndt. Wave–particle duality of C60 molecules (англ.) // Nature. — 1999. — Vol. 401, no. 6754. — P. 680—682. — doi:10.1038/44348.
- ↑ H.F.; Schouten. Plasmon-Assisted Two-Slit Transmission: Young's Experiment Revisited (англ.) // Phys. Rev. Lett. : journal. — 2005. — 7 February (vol. 94, no. 5). — doi:10.1103/physrevlett.94.053901. — . — PMID 15783641.
- ↑ Roger; Bach et al. Controlled double-slit electron diffraction (англ.) // New Journal of Physics?! : journal. — 2013. — March (vol. 15, no. 3). — doi:10.1088/1367-2630/15/3/033018. — . — arXiv:1210.6243.
- ↑ 1 2 John WM; Bush. Pilot-wave hydrodynamics (англ.) // Annual Review of Fluid Mechanics[англ.] : journal. — Annual Reviews, 2015. — Vol. 47, no. 1. — P. 269—292. — doi:10.1146/annurev-fluid-010814-014506. — .
- ↑ John W. M.; Bush. Quantum mechanics writ large (англ.) // Proceedings of the National Academy of Sciences of the United States of America : journal. — 2010. — Vol. 107, no. 41. — P. 17455—17456. — doi:10.1073/pnas.1012399107. — .
- ↑ Natalie Wolchover, Quanta Magazine, Science, 06.30.14. Have We Been Interpreting Quantum Mechanics Wrong This Whole Time? (англ.) // Wired : journal. — 2014. — 30 June.
- ↑ Y.; Couder. Probabilities and trajectories in a classical wave-particle duality (англ.) // Journal of Physics: Conference Series[англ.] : journal. — 2012. — Vol. 361, no. 1. — doi:10.1088/1742-6596/361/1/012001. — .
- ↑ Pengyun; Li. Classical hypercorrelation and wave-optics analogy of quantum superdense coding (англ.) // Scientific Reports[англ.] : journal. — 2016. — Vol. 5. — P. 18574. — doi:10.1038/srep18574. — . — PMID 26689679.
- ↑ Jenkins FA and White HE, Fundamentals of Optics, 1967, McGraw Hill, New York
- ↑ Longhurst RS, Physical and Geometrical Optics, 1967, 2nd Edition, Longmans
- ↑ Carlo[англ.]. Relational Quantum Mechanics (англ.) // International Journal of Theoretical Physics[англ.] : journal. — 1996. — Vol. 35, no. 8. — P. 1637—1678. — doi:10.1007/BF02302261. — . — arXiv:quant-ph/9609002.
- ↑ Thomas; Filk. Relational Interpretation of the Wave Function and a Possible Way Around Bell's Theorem (англ.) // International Journal of Theoretical Physics[англ.] : journal. — 2006. — Vol. 45, no. 6. — P. 1205—1219. — doi:10.1007/s10773-006-9125-0. — . — arXiv:quant-ph/0602060.
- ↑ C.; Philippidis. Quantum interference and the quantum potential (англ.) // Il Nuovo Cimento B[англ.] : journal. — 1979. — Vol. 52, no. 1. — P. 15—28. — ISSN 1826-9877. — doi:10.1007/bf02743566. — .
- ↑ Bohmian Mechanics // The Stanford Encyclopedia of Philosophy (неопр.). — Metaphysics Research Lab, Stanford University, 2017.
Внешние ссылки
Интерактивные анимации
Эксперименты с одной частицей
- Сайт с фильмом и другой информацией о первом одноэлектронном эксперименте Мерли, Миссироли и Поцци.
- Фильм, показывающий одноэлектронные события, формирующие интерференционную картину в экспериментах с двумя щелями. Несколько версий с и без повествования (размер файла = от 3,6 до 10,4 МБ) (длина видеоролика = 1м 8с)
- Freeview видео "Электронные волны раскрывают микрокосмос". Дискурс Королевского института Акиры Тономуры, предоставленный Vega Science Trust
- Сайт Hitachi со справочной информацией о видео Tonomura и ссылкой на видео
Гидродинамический аналог
- "Одночастичная интерференция, наблюдаемая для макроскопических объектов"
- Гидродинамика пилот-волны: дополнительное видео
- Сквозь червоточину : Ив Кудер. Объясняет дуальность волн/частиц с помощью кремниевых капель




![{\displaystyle {\begin{aligned}I(\theta )&\propto \cos ^{2}\left[{\frac {\pi d\sin \theta }{\lambda }}\right]~\mathrm {sinc} ^{2}\left[{\frac {\pi b\sin \theta }{\lambda }}\right]\end{aligned}}}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/5fb832693cac4bc3093639a4c6ccf7916e76a06a)


