Ломаная

Ломаная A₁A₂A₃A₄A₅A₆

Ло́маная, ломаная линия — геометрическая фигура, состоящая из отрезков, последовательно соединённых своими концами.

Определение

Ломаной (ломаной линией) $A_{1}A_{2}\dots A_{n}$ называется фигура, которая состоит из отрезков $[A_{1}A_{2}]$, $[A_{2}A_{3}]$, …, $[A_{n-1}A_{n}]$.

Точки $A_{1}$, …$A_{n}$, называются вершинами ломаной, а отрезки $[A_{1}A_{2}]$, $[A_{2}A_{3}]$, …, $[A_{n-1}A_{n}]$ — звеньями ломаной.

Ломаная называется невырожденной, если для любого $k\in \{1,2,\dots ,n-2\}$ отрезки $[A_{k}A_{k+1}]$ и $[A_{k+1}A_{k+2}]$ не лежат на одной прямой; в противном случае — вырожденной.

Типы ломаных

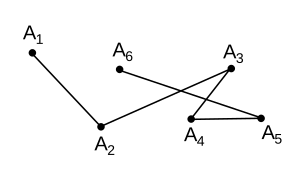
• Ломаная имеет самопересечение, если хотя бы два её звена имеют общую точку помимо общей вершины:

Изображённую здесь ломаную следует называть «ломаная A₁A₂A₃A₄A₅A₆».

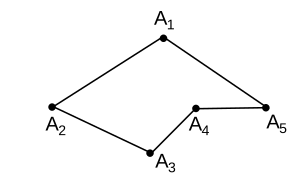
• Ломаная называется замкнутой, если первая и последняя точки ломаной совпадают; в этом случае дополнительно требуют, чтобы отрезки $A_{1}A_{2}$ и $A_{n-1}A_{n}$ также не лежали на одной прямой:

Замкнутую плоскую ломаную часто называют многоугольником: в этом случае изображённая ломаная A₁A₂A₃A₄A₅A₁ будет называться «многоугольник» A₁A₂A₃A₄A₅», а звенья будут называться сторонами многоугольника. В ряде случаев, например, при рассмотрении многогранников, стороны многоугольника называются рёбрами.

См. также

• Многоугольник