Кубик Рубика

Кубик Рубика Магический кубик
Bűvös kocka
Основная информация
Изобретатель	Эрнё Рубик
Год выпуска	1974
Кол-во возможных комбинаций	43 252 003 274 489 856 000
Форма	куб

Классический кубик Рубика 3×3×3 в собранном виде

Ку́бик Ру́бика (первоначально «магический кубик», венг. bűvös kocka) — механическая головоломка, изобретённая в 1974 году (и запатентованная в 1975 году) венгерским скульптором и преподавателем архитектуры Эрнё Рубиком.

Головоломка представляет собой пластмассовый куб 3×3×3 (в первоначальном варианте) с 54 видимыми цветными наклейками. Грани большого куба способны вращаться вокруг 3 внутренних осей куба. Каждая из шести граней состоит из девяти квадратов и окрашена в один из шести цветов, в одном из распространённых вариантов окраски, расположенных парами друг напротив друга: красный — оранжевый, белый — жёлтый, синий — зелёный. Повороты граней позволяют переупорядочить цветные квадраты множеством различных способов. Задача игрока заключается в том, чтобы «собрать кубик Рубика»: поворачивая грани куба, вернуть его в первоначальное состояние, когда каждая из граней состоит из квадратов одного цвета.

Название «Кубик Рубика» принято в большинстве языков мира, за исключением немецкого и китайского, где распространённым осталось его первоначальное наименование «Магический куб» (нем. Zauberwürfel; кит. 魔方 [мофан]), а также иврита, где его называют «венгерским кубиком» (ивр. קובייה הונגרית‎).

История

Принцип устройства изобретения на магнитах патента US3655201

Оригинальная упаковка венгерского кубика Рубика, 1982 год

5×5×5 (Профессорский кубик)

4×4×4 (Месть Рубика, Мастер-кубик)

2×2×2 (Карманный кубик)

Цифровой вариант Кубика Рубика (Судоку кубик)

Устройство кубика

История кубика Рубика началась в марте 1970 года, когда Ларри Николс изобрел куб-головоломку 2×2×2 с вращающимися частями, собранными на магнитах. Изобретатель сразу подал заявку на оформление канадского патента и уже 11 апреля 1972 года Николс получил американский патент под номером 3655201 (позднее, в 1986 году апелляционный суд подтвердил, что карманный кубик Рубика 2×2×2, по причине сходства изобретений, нарушает авторские права Николса). 9 апреля 1970 года Франк Фокс подаёт заявку на сферическую головоломку 3×3×3, и 16 января 1974 года получает патент (1344259).

В середине 1970-х Эрнё Рубик работал в отделе Дизайна интерьера в академии Прикладного искусства в Будапеште. Ему никак не удавалось втолковать студентам математическую теорию групп. Занимаясь группами, Рубик однажды сделал 27 деревянных кубиков, раскрасил каждый в шесть цветов. Неожиданно оказалось довольно трудно сложить из них один куб, чтобы каждая грань была окрашена в свой цвет. Сам Рубик бился над задачей целый месяц (хотя сообщается, что первый кубик Рубика был построен как обучающий инструмент, чтобы помочь его студентам понять трехмерные объекты, фактически первоначальная цель Рубика заключалась в решении проблемы структурного перемещения независимых частей). Но самым сложным оказалось придумать механизм, который состоял из 26 кубиков (в центральном не было необходимости) и структурного крепления. 30 января 1975 года Э. Рубик получил венгерский патент (HU170062) на своё изобретение, «Магический кубик» (Bűvös kocka).

Первые партии кубиков Рубика были выпущены в конце 1977 года для Будапештского магазина игрушек. Игрушкой совершенно случайно заинтересовался^{[когда?]} немецкий компьютерный предприниматель венгерского происхождения Тибор Лаци (зайдя в кафе во время деловой поездки в Венгрию выпить кофе, он увидел занимательную вещицу в руках у официанта). Увлекающийся математикой Лаци пришёл в восхищение от игрушки и буквально на следующий день прибыл уже в государственную торговую фирму Konsumex и предложил продавать кубик на Западе. Тогда же он познакомился и с Рубиком. Заинтересованный Тибор Лаци вышел на владельца Seven Towns Ltd., англичанина Тома Кремера (Tom Kremer), также венгра по линии матери. Кремер взялся добиться привлечения интереса к разноцветному чуду.

В сентябре 1979 года, на переговорах в Будапеште, был заключён договор с крупной американской компанией Ideal Toy Corporation (позже куплена корпорацией CBS) на поставку в США одного миллиона кубиков. В процессе переговоров всплыла ещё одна проблема — Кубик был запатентован лишь в Венгрии. Американцы же могли торговать товарами, авторские права на которые официально зарегистрированы на территории США. Чтобы хоть как-то уладить это препятствие, в самом начале 1980-го «Магический куб» (Magic Cube) решено было переименовать в кубик Рубика (Rubik’s Cube).^{[прояснить]}

Стараниями Лаци и Кремера в январе — феврале [1980 год]а состоялся международный дебют кубика. В феврале 1980 года головоломка дебютировала на ярмарках игрушек Лондона, Парижа, Нюрнберга (Nuremberg Toy Fair) и Нью-Йорка. Американская премьера состоялась 5 мая в Голливуде, а представляла кубик венгерская кинозвезда Габор. Следующие два года стали временем всемирного помешательства, в связи с дефицитом кубов стали производиться подделки в самых разных странах. Только до конца 1982 г. было продано свыше 100 миллионов официальных кубиков и в полтора раза больше подделок. Никаких проблем со сбытом головоломки не было, были проблемы с производством. Венгрия физически не могла делать больше нескольких миллионов штук в год. Фабрики по изготовлению кубиков открываются в Гонконге, Тайване, Коста-Рике и Бразилии. В Советский Союз кубик пришёл в 1981 г.

В 1980 году Кубик Рубика получил венгерский национальный приз за лучшее изобретение и выиграл конкурсы на лучшую игрушку в США, Великобритании, Германии, Франции. Популярность головоломки росла. Сложность сборки кубика вызвала к жизни поток специальных изданий по проблеме: было выпущено более 60 книг. От непрерывной многочасовой игры у людей попросту сводило запястья. Во многих ресторанах кубик входил в число обязательных предметов сервировки стола наряду с солонкой и перечницей. Появилось «Искусство кубика Рубика» (Rubik’s Cube Art) — художники собирали не только сами кубики, но уже из кубиков собирали свои произведения. В 1981 году в Англии проходит церемония представления кубика принцу Чарльзу и леди Диане (тогда же выходит ограниченным тиражом версия, посвящённая их свадьбе, состоявшейся 29 июля 1981, «Royal Puzzle»), головоломка попадает в экспозицию Нью-йоркского музея современного искусства, а годом позже кубик Рубика попадает в Оксфордский словарь.

Сегодня права на кубик Рубика и другие головоломки Эрнё Рубика принадлежат английской компании Seven Towns Ltd., которой уже 40 лет владеет близкий друг Эрнё Рубика — Том Кремер. Под контролем англичан кубик Рубика производится и продаётся во всем мире. Первые оригинальные кубики Рубика были целиком из цельного пластика. Позже стали производить детали, используя полость внутри. Подавляющее большинство головоломок производится в Китае (иногда в Тайване или Гонконге). Также головоломки делают в Германии (Мефферт), Японии (Кацухико Окамото), Греции (Вердес Панайиотис, V-cube), Украине (Разумный кубик/Smartcube, Одесский куб) и некоторые в России. До 1997 года существовал производитель в США Ideal toys, сделавший головоломку звезда Александера.

Механизм

Разобранный на части кубик Рубика

Из центральных и рёберных элементов с внутренней стороны вырезан фрагмент таким образом, что получается полость в виде объединения трёх цилиндров. Помимо этого, на рёберных и угловых элементах имеются выступы особой формы. Эти выступы образуют фрагмент цилиндра, плотно входящий в полость. Благодаря такой конструкции грани кубика свободно вращаются.

В центре конструкции вместо «невидимого кубика» находится трёхмерная крестовина, на которой свободно вращаются центральные элементы. Все остальные элементы держатся друг за друга, входя выступами в вышеуказанную выемку.

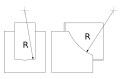
Ориентировочные безмасштабные чертежи

• 
  Центральный элемент
• 
  Рёберный элемент
• 
  Угловой элемент
• 
  Вариант крестовины с центральными элементами

В СССР в журнале «Юный техник» № 7 за 1982 год были опубликованы чертежи для самостоятельного изготовления кубика. Они отличались от известной нам конструкции и были специально рассчитаны на компоненты из дерева. В этих чертежах пазы преобладали над выступами. Однако тому, кто захотел бы собрать такой кубик, потребовались бы 27 одинаковых кубиков из бука или липы, латунные кольца, а также воск для смазывания граней.

Комбинаторика

Основные статьи: Математика кубика Рубика и Группа кубика Рубика

Число всех достижимых различных состояний кубика Рубика 3x3x3 равно:

${8!\times 3^{7}\times {\frac {12!}{2}}\times 2^{11}}=$ 43 252 003 274 489 856 000

Данное число учитывает перестановки, которые могут быть достигнуты поворотами сторон куба, а если учесть также нелегальные состояния, которые могут быть получены при физической разборке куба на детали и сборки обратно, то число состояний станет в двенадцать раз больше:

${8!\times 3^{8}\times 12!\times 2^{12}}=$ 519 024 039 293 878 272 000

Если учитывать ориентацию центральных квадратов, то количество возможных состояний возрастает в 4⁶/2 = 2048 раз. Однако при сборке кубика ориентацию центральных квадратов почти никогда не учитывают, поскольку на большинстве обычных кубиков Рубика нет пометок, которые позволяли бы её отслеживать.

Алгоритм Бога

Основная статья: Алгоритм Бога

История поиска алгоритма Бога для кубика Рубика началась не позже 1980 года, когда открылся список рассылки для любителей кубика Рубика. С тех пор математики, программисты и просто любители стремились найти алгоритм, который бы позволил решать кубик Рубика за минимальное число ходов.

В июле 2010 года программист из Пало-Альто Томас Рокики, учитель математики из Дармштадта Герберт Коцемба, математик из Кентского университета Морли Дэвидсон и инженер компании Google Inc. Джон Детридж доказали, что каждая конфигурация кубика Рубика может быть решена не более чем в 20 ходов. При этом любой поворот грани считался одним ходом. Таким образом, число Бога в метрике FTM оказалось равно 20 ходам.

Скоростная сборка

Скоростная сборка кубика Рубика одной рукой

Сборка кубика Рубика ногами

Люди, увлекающиеся скоростной сборкой кубика Рубика, называются спидкуберами. А сама скоростная сборка — спидкубинг (англ. speedcubing).

На данный момент одним из самых популярных методов скоростной сборки является метод Джессики Фридрих. Более продвинутые спидкуберы изучают алгоритмы, объединяющие 2 этапа сборки последнего слоя в один.

Официальные соревнования по скоростной сборке кубика Рубика регулярно проводятся Всемирной ассоциацией спидкубинга(WCA). Каждые 2 года проходят чемпионаты Европы, Азии, а так же чемпионат мира.

Согласно правилам WCA, перед сборкой кубы должны быть перемешаны по алгоритму (scramble), сгенерированному компьютером с помощью программы TNoodle (для куба 3×3×3, для других головоломок есть отдельные программы генерации скрамблов). При этом у всех участников начальные позиции перемешанного кубика (скрамблы) должны быть одинаковыми.

Победитель определяется не по результату единичной сборки, а по среднему времени из 5 попыток, при этом лучшая и худшая попытки не учитываются, а вычисляется среднее из оставшихся трёх. Однако в других дисциплинах могут использоваться и другие варианты: среднее из 3 (например, для куба 7×7×7), лучшее из 3 (сборка вслепую).

Также спидкуберы могут собирать кубик Рубика одной рукой или ногами.

Официальные соревнования в наше время проводятся в следующих категориях:

Категория	Тип Кубика
Скоростная сборка	2×2×2, 3×3×3, 4×4×4, 5×5×5, 6×6×6, 7×7×7
Сборка одной рукой	3×3×3
Сборка вслепую	3×3×3, 4×4×4, 5×5×5
Сборка на количество ходов	3×3×3

Текущие рекорды

В классической дисциплине (кубик 3×3×3) действующий рекорд 3,47 секунды. Он был установлен представителем КНР Ду Юйшэном (кит. 杜宇生) 24-25 ноября 2018 года на соревновании Wuhu Open 2018 в Китае. Из соревнований, которые официально проводятся Всемирной ассоциацией спидкубинга (WCA) максимальной сложностью обладает сборка кубика 5×5×5 вслепую, действующий рекорд времени в данной дисциплине составляет 2:21.62 и принадлежит американцу Стэнли Чапелу (англ. Stanley Chapel). Остальные рекорды можно посмотреть в таблице.

Роботы

В октябре 2011 года робот CubeStormer II, специально собранный из 4 наборов конструктора Lego Mindstorms, побил рекорд человека и собрал кубик за 5,53 секунды (рекорд был установлен не в присутствии комиссии WCA, и, следовательно, официальным не является, а неофициальный рекорд, установленный человеком, ещё меньше).

В марте 2014 года созданный за полтора года инженерами Дэвидом Гилдэем (англ. David Gilday) и Майком Добсоном (англ. Mike Dobson) CubeStormer III из деталей того же конструктора Lego Mindstorms и с ARM-мозгом в виде смартфона Samsung Galaxy S4, собрал головоломку за 3,253 секунды.

В ноябре 2015 года машина, созданная Захарией Громко (Zackary Gromko), студентом из США, собрала кубик Рубика за 2,39 секунды.

В январе 2016 года Джей Флэтленд (англ. Jay Flatland) и Пол Роуз (англ. Paul Rose) из Канзаса показали свой компьютер официальному представителю Книги рекордов Гиннесса: системе хватило 0,9 секунды.

В январе 2018 года специалист по робототехнике Бен Кац (Ben Katz) и разработчик программного обеспечения Джаред Ди Карло (Jared Di Carlo) создали робота, который способен собрать кубик Рубика за 0,38 секунды.

Соревнования в России

8 марта 2009 года прошёл первый официальный чемпионат России, победителем стал Антон Ростовиков. 26—27 ноября 2011 года в Москве прошёл официальный открытый чемпионат России, в котором приняли участие около 60 человек в дисциплинах от 2×2×2 до 7×7×7, а также сборка кубика Рубика вслепую. Чемпионом в дисциплине 3×3×3 стал Рябко Сергей со средним результатом в финале 10,65 секунды. Рекорд России в единичной сборке принадлежит Андрею Че, он собрал головоломку за 5,29 секунды на чемпионате Ramenskoe Open 2019.

Чемпионат Европы 2010

С 1 по 3 октября 2010 года в Будапеште прошёл чемпионат Европы, собравший участников, соревновавшихся в различных дисциплинах. Чемпионом Европы в сборке классического кубика 3×3×3 стал российский спидкубер Сергей Рябко, опередивший в финале в том числе действующего на тот момент рекордсмена в единичной попытке Эрика Аккерсдейка, со средним временем в финале 10,31 секунды.

Чемпионат Европы 2012

С 12 по 14 октября 2012 года во Вроцлаве (Польша) прошёл чемпионат Европы. Чемпионом второй раз подряд стал участник из России Сергей Рябко, опередивший чемпиона мира. Среднее время Сергея составило 8,89 сек.

Варианты

• 
  Варианты кубика Рубика
• 
  С удлинёнными элементами
• 
  Крейзи кубик
• 
  Кубик Рубика для слепых со шрифтом Брайля
• 
  Электронный кубик Рубика без физического вращения
• 
  Мазекуб

Иллюстрация сборки на примере кубика 2x2

Кубик Рубика 17×17×17

Помимо традиционного 6-цветного исполнения кубика 3×3×3 встречаются 2×2×2, 4×4×4, 5×5×5, 6×6×6, 7×7×7, 8×8×8, 9×9×9, 10×10×10, 11×11×11, 12x12x12, 13×13×13, 14x14x14, 15×15×15, 16x16x16, 17×17×17 , 19x19x19, 21x21x21; кубики с изображениями на гранях или просто нетрадиционной расцветкой; «гибриды», полученные объединением нескольких кубиков, варианты с тетраэдрами, с разным числом деталей в слоях, закруглёнными углами или вообще причудливой формы. Куб со стороной 4 часто называют мастер-кубом (англ.) или «Реваншем Рубика» («местью Рубика»).

После сборки до подобного положения куб 5×5×5 («Профессорский») рассматривается как трёхслойный и дальше собирается как куб 3×3×3. Для кубиков большего размера — то же самое

Алгоритмы сборки гигантских кубиков Рубика сводятся к алгоритму сборки кубика Рубика 3×3×3.

На данный момент самым большим в массовом производстве «не виртуальным» кубиком Рубика является кубик Рубика 21x21x21. Однако рекордсменом является кубик 33×33×33. Этот же человек создал кубоид 1x2x111. Чем больше по числу малых кубиков кубик Рубика, тем обычно труднее и дольше его собирать. Однако в то же время есть и доля единообразия в сборке кубиков различной величины, поскольку популярные методы сборки больших кубиков Рубика (4×4×4, 5×5×5 и т. д.) основаны на редукции, то есть сведении сборки такого кубика к сборке кубика 3×3×3.

Также существуют кубики Рубика для слепых, сборка которых основывается не на визуальном, а тактильном ощущении поверхностей кубика, то есть вместо цветов используется рельефная поверхность.

Одной из последних модификаций кубика Рубика является Зеркальный кубик Рубика, с размером массива 3×3×3, как и в оригинальной версии головоломки, однако выполненный со всеми гранями одного цвета (часто блестящими, зеркальными — откуда и название), но на каждой из которых вместо квадратов — прямоугольники разных размеров.

Другие формы

• 
  Куб Фишера
• 
  Мегаминкс
• 
  Пирамидка Мефферта
• 
  Гигаминкс
• 
  Тераминкс
• 
  Рубик домино
• 
  Плоский кубик Рубика
• 
  Кубик с пустотой
• 
  Кубик Рубика 3x3x5
• 
  Сборка кубиков Рубика 3x3x4 и 3x3x5
• 
  Кубик Рубика 2x2x3
• 
  Кубик Рубика 3x3x2
• 
  Сдвоенный кубик Рубика

Кубик Октостар с элементами разной формы

Кубик 3x3x7 с элементами разной формы

Зеркальный кубик Рубика в несобранном виде

Разнообразие версий и их сочетаний

Существует множество головоломок, аналогичных кубику Рубика по устройству, но имеющих другую форму:

• Куб Фишера — механизм кубика повернут на 45° относительно одной из осей.
• Куб Мельница — механизм кубика повернут на 31,3° относительно одной из осей.
• Модификации «Crazy» для кубов Фишера и Мельницы. Механизм в таких кубах дополнительно повёрнут по остальным двум осям.
• Куб Аксис — механизм кубика повернут на одинаковую величину вокруг всех трех осей.
• Зеркальные кубы 3х3х3, 2х2х2 и 4х4х4. Механизм кубика сдвинут в направлении одного из углов, в результате чего элементы имеют разный размер. Как правило, такие кубы одноцветные и покрыты светоотражающими наклейками, откуда и название.
• Куб «Призрак» (Ghost cube) — одна из сложнейших в сборке модификаций. Сложность состоит в том, что вращение по всем трем осям доступно только после сдвига центрального слоя, то есть собирать куб нужно именно с таким сдвинутым положением среднего слоя. Плюс к этому, все 26 элементов имеют различную форму, а сам куб одноцветный. В серийном производстве есть призрак 2х2х2 и 3х3х3. 4х4х4 существуют только сделанные вручную или при помощи трехмерной печати. 5х5х5 и далее сделать можно, но детали будут либо с криволинейными разрезами, либо непропорциональными.
• Различные модификации 3х3х3 в форме яйца, яблока, банана, звезды, сердечка и т. п. Как правило, тоже одноцветны.
• Куб Скваер. Имеется 2 различные модификации. Есть также головоломка «Наутилус» со схожим механизмом, где все сектора имеют различный размер.
• Супер Скваер. Бывает двухслойным или четырехслойным. Есть разновидность двухслойного Супер Скваера в виде 6-лучевой звезды.
• Кубоиды 1х1х3, 1х2х3, 3x3x1, 2х2х3, 2х2х4, 2х2х5, 2х2х6, 2х2х7, 2х3х4, 3х3х2, 3х3х4, 3х3х5, 3х3х6, 3х3х7, 3х3х8, 4х4х3, 4х4х5, 4х4х6, 5х5х4, 2х4х6 и другие. Все элементы таких кубоидов имеют визуально одинаковый кубический размер. Кубоид 3x3x1 (другое его название — «Флоп») также выпускается в форме функционирующего спиннера. Кубоид 1х2х3 имеет множество модификаций различной формы (медведь, ёлочка и другие). У кубоида 2х2х3 тоже есть различные модификации.
• Кубоиды 3х3х5 и 3х3х7 кубической формы, где слои 3х3х3 разбиты.
• Кубоид 3х3х9 и серия головоломок под названием «Дорожные блоки». Также есть варианты «Crazy».
• Кубоиды 3х3х11-3х3х17 с непропорциональными слоями. У них есть комбинации в сочетании с I-кубами, Roadblock и Crazy.
• Кубоиды Фишера 3х3х5, 3х3х7 и 4х4х6.
• I-куб 4х4х5 и его фишер-вариант.
• Серия «L-X-кросс куб» — на одну, несколько или каждую грань куба 3х3х3 добавлена полностью функциональную грань.
• Версии «Crazy» предыдущего пункта — на гранях есть круги, усложняющие сборку.
• Кубоид 3×4×5
• Бочонок Рубика — может менять форму, но в собранном виде имеет форму цилиндра.
• Диагональный пазл — по сути удлиненный с двух сторон куб Фишера, похожий на прямоугольный параллелепипед.
• Кубики 2х2х2, 3х3х3, 4х4х4 и 5х5х5 из игральных костей и магнитов вместо обычной крестовины и механизма, которые даже продаются.
• Сиамские кубы — 2 или более одинаковые головоломки (в основном, кубы 3х3х3) срощены воедино. За счет общей площади соприкосновения некоторые повороты блокируются. Некоторые изобретатели умудрились сделать полностью функциональные аналоги, где даже можно менять детали между отдельными кубами головоломки через фронтальную грань, но они используют магниты, так как при повороте передней стороны на 90 градусов угловые элементы ни за что не держатся и висят в пространстве. Сиамский 3х3х3, где бы можно было менять детали между двумя пазлами, можно сделать из двух магнитных кубиков 3х3х3. Но со временем Оскар ван Девентер все же придумал способ зафиксировать угловые детали на сиамском 2х2х2 с дополнительным функционалом при помощи защелкивающейся булавки, которая активируется и вылезает, когда грань повернута на 90 градусов, но обратно встает на место, когда поворот на 180 закончен.
• тетраэдр «Пирамидка Мефферта» («Молдавская пирамидка») или «Японский тетраэдр») — изобретена раньше кубика Рубика и является самой простой для сборки из перечисленных головоломок;
• Пираморфикс, Мастер Пираморфикс и так далее. Головоломки с устройством идентичным кубику Рубика, но имеющие форму тетраэдра и другую раскраску;
• Трансформ 3х3х3 в форму шестиугольной призмы.
• Сабля 3х3х3 — мод кубика 3х3х3 в форму ромбоэдра. Каждый поворот за счет вершин.
• Пандора-куб
• Додекаэдрон — трансформ кубика Рубика 3х3х3 в форму додекаэдра.
• Мячик 3х3х3. Может быть как в форме идеального шара, так и в форме ромбокубооктаэдра, который стремится к шару.
• октаэдр, известный как «Trajber's Octahedron 3×3×3» — головоломка, которую можно бы было назвать двойственной Кубику Рубика по аналогии с понятием двойственный многогранник;

У него есть и 4х4х4 вариант, который представляет сложность в сборке, потому что имеет множество собранных состояний. Также была попытка выпустить 4х4х4 вариант икосаэдра, но она провалилась. У прототипа некоторые детали были неправильной формы, неровными, вращения заедали.

• Face и corner turning октаэдры. Они похожи на вид, но у одного ось вращения в гранях, а у другого — в углах. Существует также октаэдр, который вращается ребрами. Его называют Самоцвет 1(Gem 1).
• Wellness куб — кубик Рубика, у которого каждая деталь — не кубик, а шарик.
• Спираль 3х3х3
• Кубик Рубика, у которого вместо наклеек плитки лего.
• додекаэдр «Мегаминкс», являющийся додекаэдрическим аналогом кубика Рубика 3×3×3 (варианты этой головоломки также имеют размерность от киломинкса, являющегося додекаэдрическим аналогом кубика 2×2, заканчивая йотаминксом)
• большой додекаэдр Звезда Александера;
• Кристал пираминкс
• Туттминкс. 32 грани — 12 пятиугольников и 20 шестиугольников. У него также есть Неразлучник(англ. Love bird) или килотуттминкс — 2х2х2 версия туттминкса, Рейминкс или гигатуттминкс — 5х5х5 туттминкс, сквозная версия без центров и в форме сферы с различными цветовыми раскрасками.
• Суперзвезда — аналог звезды Александера, проделанный с туттминксом.
• Dogic — очень редкая головоломка, которую Мефферт перестал выпускать. Является икосаэдром, который представляет собой углы мегаминкса треугольной формы и добавленные на 12 сторон по слою. В 2021 году Кельвин выпустил свой тираж. Головоломку снова стало возможно приобрести.
• Окончательный пираминкс (англ. Pyraminx ultimate) — выпущен под именем Octic. Это 3х3х5 кросс куб, у которого урезаны ребра и углы. Dogic по своей сути является той же головоломкой, проделанной с киломинксом (остальные детали мегаминкса становятся спрятанными).
• Тоже Pyraminx ultimate, но «вывернутый наизнанку». Это урезанный куб 4х4х4 и раскрашенный в 8 цветов. У pyraminx ultimate 6 квадратных сторон, являющихся дополнительными слоями. На этом пазле 8 треугольных сторон, но их нельзя повернуть просто так. Для этого надо делать ходы куба 2х2х2. То есть в данном случае дополнительные слои могут поворачиваться, но не напрямую, а только косвенно. Для этого потребуется не один ход, а массив/последовательность движений/поворотов. Такой пазл сложнее и хитрее в сборке, чем вариант Octic, и менее громоздкий, более дешевый.

Также этот пазл одновременно является 4х4х4 мячиком, так как фигура стремится к шару.

• Куб-бабочка
• Цветковый вертолет — гибрид бабочки и дино куба
• Дино куб
• Радужный куб — кубооктаэдр, у которого вращаются треугольные грани. Тот же дино куб с усеченными вершинами до середины.
• СуперХ — гибрид дино куба и 2х2х2.
• Старминкс 1 — додекаэдрический аналог дино куба.
• Старминкс 2 — более глубокий разрез кристал пираминкса. От пересечения образуются новые детали: пятиугольные центры и лепестки.
• Пышный старминкс — старминкс 2 с криволинейными/гиперболическими разрезами. Появляется новый тип деталей — углы от киломинкса.
• НЛО Рубика
• Шестеренчатый куб. Есть и другие головоломки разной формы с шестеренками.
• Сыр Рубика, есть с двумя и с тремя слоями
• Камуфляжный куб, у него есть несколько вариантов
• Колеса мудрости — кросс куб 3х3х3, у которого добавочные слоя могут вращаться на 45 градусов.
• Машина времени — кросс версия скваера-2.
• Миксап куб — кубик Рубика, у которого центральный слой можно поворачивать на 45 градусов. У него есть также усложненные версии с дополнительными детальками. Миксап есть 3х3х3, 4х4х4, 3х3х4 и 4х4х3.
• Вормхол I, II и III.
• Багуа куб — каждый крайний слой можно поворачивать как на 90, так и на 45 градусов, но иногда из-за этого могут блокироваться те или иные движения.
• Октостар — более простой багуа. Половина кусков на ребрах — цельные детали.
• Клевер куб — каждый ход меняет форму и несимметрично переставляет сегменты из нескольких деталей. У него есть аналоги октаэдра, додекаэдра и икосаэдра, а также плюс версия с некоторыми разбитыми деталями на сегментах.
• Тоже клевер куб, но у которого у каждого ребра не две оси вращения, а одна. Это куб-вертолет, у которого спрятаны угловые элементы.
• Щелкунчик — на гранях есть стрелки, их(грани) можно вращать только в направлении стрелок. Движение заблокируется, если стрелки указывают в разные стороны. Изобретен японцем Кацухико Окамото.
• Constrained кубы — на гранях стоят блокираторы, иногда не дающие сделать поворот.
• Бермуда кубы — на гранях есть треугольники или четырехугольники. Иногда они будут блокировать те или иные повороты. Некоторые детали выполнены в стиле фишер куба, что позволяет делать движения на 45 градусов.
• Little chop — кубик, визуально похожий на дино куб, но где повороты идут из ребер с максимально глубоким возможным разрезом. Механизм основан либо на магнитах и металлической сфере, либо на деталях с прорезанными рельсами и гравитационными булавками.
• Мелинда 2х2х2х2 — физический четырехмерный аналог кубика 2х2х2. Он сделан при помощи магнитов. Им можно делать все ходы и играть в третьем измерении.
• множество головоломок этих же (в особенности октаэдра) и других форм:
  • ромбододекаэдр;
  • кубооктаэдр;
  • усечённые тетраэдр и октаэдр;
  • Мастер-скьюб — на каждой из шести граней находится центральный кубик, окруженный четырьмя внутренними кубиками.
  • Профессор скьюб — следующий по счету после мастер скьюба. Чаще всего его называют «элитным скьюбом».
  • С-скьюб — визуально похож на мастер скьюб, но оси вращения лежат иначе.
  • 7-скьюб — визуально похож на профессор скьюб, но имеет другие оси вращения.
  • F-скьюб — промежуточная головоломка между скьюбом и мастер скьюбом.
    • Айви-кьюб (ivy cube) — разновидность скьюба.
  • Рекс-куб — отсутствуют вершины.
  • Глаза дьявола — 4х4х4 айви ромбододекаэдр по короткой шкале. Могут поворачиваться вершины, где сходятся 4 стороны, и в этом же направлении более глубокий слой. Вершины, где сходятся 3 стороны, не повернуть. На ребрах внутреннего 3х3х3 есть окрашенные цветами глазики, которые надо дополнительно расставить, что усложняет сборку.
  • Баугиния — аналог рекс куба, но в форме додекаэдра.
  • Twistball — дино куб в форме шара. По длинной шкале это 2х2х2 аналог баугинии, если наклеить 12 цветов, как в додекаэдре. Данный пазл выпускали разными вариантами расположения цветов, сторон и рисунков на них.
  • Radiolarian 2 — головоломка в форме икосаэдра. Двойственна баугинии.
  • Пентаграмма — похожая на баугинию головоломка, где убраны ребра, но добавлены углы, вершины. При повороте вершина, которая, казалось бы, закреплена на крестовине, смещает 3 других вершины. Это чем-то похоже на скьюб. Для сравнения, в кубике Рубика центральные элементы всегда находятся на одном и том же месте.
  • Радио додекаэдр 3 или баугиния 2 — есть и ребра из баугинии, и углы из пентаграммы. Этому пазлу двойственен Radiolarian 3.
  • Звезда Эйтана — икосаэдр, очень сложная головоломка. Является двойственной пентаграмме. 4х4х4 версия называется Туманность Эйтана.
  • Икосаикс — более простой Radiolarian 2, у которого спрятаны внутрь 60 треугольников. Они есть внутри механизма, но снаружи их не видно.
  • Радио куб 3 — икосаэдр залатали в форму куба. Еще сложнее Eitan’s star.
  • Гераниум пазлы
• прочие.

Спустя почти 30 лет после изобретения кубика Эрнё Рубик создал новую головоломку — шар Рубика, демонстрация которого состоялась на выставке в Германии в феврале 2009 года.

В 2013 году Рубик обновил механизмы кубов 3х3х3 и 2х2х2. Позже, в 2017 году, был изменен механизм кубика 4х4х4.

Компьютерные программы

Вариант электронного симулятора кубика

Вариант электронной игры с 4-х мерным кубиком 4×4×4

Виртуальные головоломки, подобные кубику Рубика, могут быть смоделированы на компьютере: от простых 2×2×2, 3х3х3 до очень сложных вариантов (100×100×100 или 1000×1000×1000 кубиков), невозможных в физическом мире — 4-, 5-, и даже 7- мерные аналоги.

Существуют компьютерные игры, моделирующие «Магический кубик», но они не получили, по сравнению с оригинальной механической головоломкой, широкого распространения. Одним из мощнейших эмуляторов, где можно собирать даже те головоломки, которых никогда не существовало в природе в каком-либо виде, является pCubes.

Гаджеты и игровые устройства

В 2018 году две независимые команды разработчиков представили электронные версии кубика Рубика. Группа из Тель-Авива (Израиль) представила GoCube — спортивный гаджет аналог Кубик Рубика подключающийся через BlueTooth к планшету. Также 13-летний изобретатель из Новато (США) совместно с отцом представил версию кубика Рубика 2x2x2: WOWCube с 24-экранами и несколькими играми, работающими в качестве игровой консоли.

Кубик Рубика в культуре

Мозаика на стене здания

Фигура на карнавале

Кубик Рубика оказал влияние на культуру, искусство, архитектурные композиции, некоторые обычаи.

Моддинг шарнирных головоломок

Помимо сборки головоломок(в том числе и на скорость) есть еще увлечение в сфере вращабельных головоломок, заключающееся в том, чтобы трансформировать один пазл в другой. Принцип заключается в том, чтобы что-то наклеить или сточить с головоломки(реже-самому выточить механизм или создать с нуля), чтобы из нее сделать какую-то другую головоломку. Тем самым можно сделать головоломку самому вручную без 3д печати. Иногда те или иные головоломки делают руками, так как их нет в продаже и чтобы достать пазл, необходимо его делать вручную.

Первый человек, который начал делать головоломки вручную из других головоломок, - британец Тони Фишер. Самым первым самодельным кубиком по типу кубика Рубика был сиамский кубик Рубика, который был сделан из 2 кубиков Рубика 3х3х3. В дальнейшем он сделал более 100 головоломок вручную, включая предыдущий рекорд Гиннеса, кубик Рубика с длиной ребра более 2 метров. После Тони Фишера множество других людей по свету тоже стали делать головоломки из серии кубика Рубика. Сейчас число таких головоломок - несколько тысяч видов.

Чаще всего материалом для наращивания или заполнения деталей выступает эпоксидная смола(эпоксилин). Обыкновенно головоломки из других головоломок делаются путем спиливания некоторых частей(при этом не повредив механизм), заполнением дыр или же наращиванием деталей. Примером может быть кубик Фишера, где сначала на кубике Рубика 3х3х3 делается 4 среза, а затем другие детали наращиваются, чтобы снова получить куб.

Одни из самых популярных самодельных головоломок - кубоиды(аналоги кубика Рубика с разным числом клеток, где хотя бы одно измерение имеет отличную от оставшихся размерность). Механизмы кубоидов базируются на методе Тони Фишера для самодельных кубоидов. Принцип данного метода - полное или частичное обрезание слоя под круг и покрывание этой внутренней двигающейся крестовины внешними кубиками.

В русскоязычной среде больше всего головоломок вручную сделал Илья Топор-Гилка. Самые крупные его самодельные головоломки - кубоид 54х54х36 в форме бочонка(таблетки), боковые грани которого раскрашены в 16 цветов, который на самом деле является универсальной("собирательной") головоломкой и содержит в себе множество других, и кубоид 54х54х36 в форме сплюснутого эллипсоида(сумасшедшая пилюля или crazypill). Сам Илья Топор-Гилка почти всегда старается делать головоломки "большими порциями"("фермерские" головоломки), например, максимально возможный пазл в семействе или чтобы пазл сразу охватывал несколько семейств головоломок, тем самым как бы "отчитавшись" и "отыгравшись" за все предыдущие. Как говорит изобретатель, это "более эффективно" и позволяет сделать(вернее, охватить) максимально много головоломок, при этом затратив в несколько раз меньше сырья и времени.

Головоломки, изобретенные Ильей Топор-Гилка(все сделаны вручную):

Кубоид 6х6х5, каждый кубик 11х13,2 миллиметра, но на глаз кажется, что это пропорциональный кубоид.

Рекс куб с прямыми разрезами

Звезда 3х3х3 с 6 вершинами. Делается из 2 звезд с 5 вершинами путем перестановки деталей.

Радужный ромбический F-додекаэдр. Ромбододекаэдрический аналог промежуточной головоломки между радужным кубом и мастер радужным кубом.

Пропорциональный зеркальный кубоид 3х3х5

Пропорциональное пасхальное яйцо 3х3х3

Пропорциональный кубоид 6х6х4, каждый кубик 11 миллиметров. Илья Топор-Гилка попытался сделать меньшие порции, но 5х5х3 сделать не удалось, а 4х4х2 вращался слишком туго и ломался. Сам Илья Топор-Гилка относит пропорциональные кубоиды 4х4х2 и 5х5х3 к головоломкам, которые делаются через так называемый "белый оллзинг".

Пропорциональный кубоид 7х7х5, каждый кубик 10 миллиметров.

Пропорциональный двухслойный профессор ментальный флоп

Гигантский ментальный флоп

Гигантский дорожный блок 1х1х2

Ромбододекаэдрический миксап скьюб плюс - куб 3х3х3 Миксап плюс, трансформированный в форму ромбододекаэдра.

Зеркальный флоп I-кубоид 2х2х3

Пропорциональный зеркальный кубик 5х5х5

Пропорциональный зеркальный кубоид 4х4х5

Мини сквозной мыльный батончик 3х9х15 - максимальное и единственное целочисленное решение Диофантового уравнения для трехосного эллипсоида, кроме 1х3х5.

Ромбододекаэдрический мастер самоцвет 4 - 6х6х6, усеченный до формы ромбикубооктаэдра.

Ромботриаконтаэдрический мастер самоцвет 4 - усеченный тераминкс.

Киломоид

Окончательная пирамидка Джингса

Гигантская дипирамидка-привидение размером более 10 сантиметров

Императорский окончательный пираминкс наизнанку - 8х8х8 с усеченными углами и шестерками ребер и раскрашенный в 8 цветов. Каждый из 8 блоков - треугольная сторона.

Кросс октаэдр Трайбера

Ромбододекаэдрический аксис F-скьюб - мастер аксис куб в форме ромбододекаэдра.

Мини десятиугольная призма 25х25х25 - мегамоид в форме десятиугольной призмы.

Профессор изумруд - следующий в линейке после изумруда и самоцвета 3.

Сквозной полулучевик 15 - скьюб в форме икосаэдра с дырками на месте треугольных центров.

Алмаз Атлантиды - модификация куба-призрака 2х2х2 в форму алмаза.

Перочинный ножик 3х3х3 - мини брелок 3х3х3 30мм в форме ромбоэдра.

Мастер двенадцатиугольная дипирамидка - куб 4х4х4 в форме двенадцатиугольной дипирамиды.

Мини кубоид 5х5х4, каждый кубик 12 миллиметров

Двенадцатигранник плюща - тот же Twistball, который обклеен в 12 цветов, как додекаэдр. Является додекаэдрическим аналогом Айви-куба.

Мини биаксис куб

Face turning кубооктаэдр

Гигантский дино скьюб - полный гибрид дино куба и скьюба гигантского размера.

Мини пропорциональный 5х5х5 кросс куб

Гигантский кубоид 5х5х4, каждый кубик 18 миллиметров

Гигантский кубоид 5х5х6, каждый кубик 18 миллиметров

Гигантский кубоид 4х4х6, каждый кубик 16,5 миллиметров

Скубтура 9х9х9

Бриллиантовый ромбододекаэдр - ромбододекаэдрический аналог промежуточной головоломки между золотым кубом Тони Фишера и платиновым кубом Бена Стритера.

Пятикратная императорская шестнадцатиугольная призма - куб 4х4х4, на который сбоку доклеены кубики из других 4х4х4, из них 32 целых и 32 половинчатых. Каждая наклейка поделена на 81 часть и является квадратом 9х9. Боковая поверхность имеет 16 сторон, каждая разного цвета. Головоломка является сегментом(4 средними слоями) гораздо бОльшей по размеру головоломки, которая делается таким же образом, но из кубоида 4х4х12. Данная головоломка является сразу несколькими головоломками:

1)Содержит в себе шестнадцатиугольную призму, сама является 9х9х9 аналогом 2)Содержит в себе пропорциональный кубоид 6х6х4 в форме бочонка 3)Является пропорциональным бочонком 54х54х36 и содержит все предыдущие бочонки. 4)Является девятикратным кросс кубоидом 54х54х18(с 9 добавочными слоями с каждой стороны) в форме бочонка 5)Общая головоломка для семейства призм и кубоидов-бочонков(таблеток) 6)Является иллюстрацией теории чисел и Диофантовых уравнений для семейства призм и головоломок в форме бочонков. Для Диофантового уравнения кубоидов-флопов в форме бочонка это максимальное решение в натуральных числах.

Сумасшедшая пилюля 54х54х36 - заданный кубоид в форме сплюснутого эллипсоида. Название взято с головоломки, сделанной канадцем Дэном Фастом, являющейся кубоидом 4х4х6 в форме растянутого эллипсоида. Форма сплюснутого эллипсоида напоминает игровую фишку. Для усложнения сборки был выбран вариант наклеек из 8 цветов,также на центральные квадраты были наклеены наклейки бирюзово-серого оттенка, чтобы искусственно создать сквозную головоломку. Илья Топор-Гилка следовал логике, что в сквозных головоломок через дырки не видно вообще ничего, кроме темноты серо-бирюзового(для белого пластика) или черного(для черного пластика) цветов.

См. также

• Волшебные кольца
• Змейка Рубика
• Часы Рубика
• Шар Рубика
• Революция Рубика
• Square One
• Gear Cube
• Скьюб
• «Рубик — удивительный кубик»
• Тетрис
• Минус-кубик

Литература

• М. Мыльников. Всем кубикам кубик // Юный техник. — 1982. — № 7.
• И. Константинов. Векторное сложение кубика (рус.) // Наука и жизнь. — 1999. — № 5.
• А. Карасев. Как научиться собирать кубик Рубика в объёме (рус.) // Наука и жизнь. — 1999. — № 5.
• И. Константинов. Собрать кубик? Это несложно! // Наука и жизнь. — 1983. — № 5. — С. 104.
• В. Залгаллер, С. Залгаллер. Венгерский шарнирный кубик // Квант. — 1980. — № 12. — С. 17—21.
• В. Дубровский. Алгоритм волшебного кубика // Квант. — 1982. — № 7. — С. 22—25.

• К. Кноп «Кубик Рубика: штурм твердыни, и снова о кубике». Компьютерра.
• Membrana.Ru: «Рубик и его кубик: раскрутка, сказочное везение, возвращение»
• Публикации из журналов «Наука и жизнь», «Квант», «Юный техник»: алгоритмы, пасьянсы на кубике, каталог вращений кубика.
• Кубик Рубика и проблема Хигмана. Материалы 20-й летней конференции международного математического Турнира городов.
• Э. Рубик. Кубик Рубика. За гранями головоломки, или природа творческой мысли = Cubed: The Puzzle of Us All (рус.) / Ernő Rubik; пер. с англ. Д. Маслов, А. Маслов. — М.: Альпина Паблишер, 2021. — 182 с. — ISBN 978-5-907394-81-0.

Ссылки

• Алгоритмы сборки кубика Рубика для размеров от 2×2×2 до 7×7×7
• 10 фактов о кубике Рубика // Популярная механика
• 5 шагов по сборке кубика Рубика 2х2х2 // Алгоритм сборки

Тематические порталы

• World Cube Association (англ.)
• Rubik’s Official Website (англ.)

Программы

• RubikCube — 3D кубик Рубика для Windows
• Сборка кубика Рубика для любого случая — составление схемы сборки кубика Рубика на основе его конфигурации
• MagicCube4D — кубик Рубика в 4 и более измерениях, на гиперкубе
• Cube Explorer — поиск решений, близких к минимальным по количеству ходов