Обратная функция

Не следует путать с Обратная величина.

Функция $f$ и обратная ей функция $f^{-1}$. Если $f(a)=3$, то $f^{-1}(3)=a$

Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией. Например, если функция от x даёт y, то обратная ей функция от y даёт x. Обратная функция функции $f$ обычно обозначается $f^{-1}$, иногда также используется обозначение $f^{\mathrm {inv} }$.

Функция, имеющая обратную, называется обратимой.

Определение

Функция $g:Y\to X$ называется обратной к функции $f:X\to Y$, если выполнены следующие тождества:

• $f(g(y))=y$ для всех $y\in Y;$
• $g(f(x))=x$ для всех $x\in X.$

Связанные определения

• Функция $g:Y\to X$ называется левой обратной к функции $f:X\to Y$, если $g(f(x))=x$ для всех $x\in X$.
• Функция $g:Y\to X$ называется правой обратной к функции $f:X\to Y$, если $f(g(y))=y$ для всех $y\in Y$.

Существование

Чтобы найти обратную функцию, нужно решить уравнение $y=f(x)$ относительно $x$. Если оно имеет более чем один корень, то функции, обратной к $f$ не существует. Таким образом, функция $f(x)$ обратима на интервале $(a;b)$ тогда и только тогда, когда на этом интервале она взаимно-однозначна.

Для непрерывной функции $F(y)$ выразить $y$ из уравнения $x-F(y)=0$ возможно в том и только том случае, когда функция $F(y)$ строго монотонна (см. теорема о неявной функции). Тем не менее, непрерывную функцию всегда можно обратить на промежутках её строгой монотонности. Например, ${\sqrt {x}}$ является обратной функцией к $x^{2}$ на $[0,+\infty )$, хотя на промежутке $(-\infty ,0]$ обратная функция другая: $-{\sqrt {x}}$.

Для существования обратной функции не являются необходимыми ни непрерывность, ни монотонность исходной функции. Пример: функция $y=x+D(x),$ где $D(x)$ — функция Дирихле, разрывна и не монотонна, однако обратная для неё существует: $x=y-D(y).$

Примеры

• Если $F:\mathbb {R} \to \mathbb {R} _{+},\;F(x)=a^{x}$, где $a>0,a\neq 1,$ то $F^{-1}(x)=\log _{a}x.$
• Если $F(x)=ax+b,\;x\in \mathbb {R}$, где $a,b\in \mathbb {R}$ фиксированные постоянные и $a\neq 0$, то $F^{-1}(x)={\frac {x-b}{a}}.$
• Если $F(x)=x^{n},x\geq 0,n\in \mathbb {Z}$, то $F^{-1}(x)={\sqrt[{n}]{x}}.$

Свойства

Графики функции и обратной ей

• Областью определения $F^{-1}$ является множество $Y$, а областью значений — множество $X$.
• По построению имеем:

$y=F(x)\Leftrightarrow x=F^{-1}(y)$

или

$F\left(F^{-1}(y)\right)=y,\;\forall y\in Y$,

$F^{-1}(F(x))=x,\;\forall x\in X$,

или короче

$F\circ F^{-1}=\mathrm {id} _{Y}$,

$F^{-1}\circ F=\mathrm {id} _{X}$,

где $\circ$ означает композицию функций, а $\mathrm {id} _{X},\mathrm {id} _{Y}$ — тождественные отображения на $X$ и $Y$ соответственно.

• Такое отображение $G\colon \,Y\to X$, что $F\circ G=\mathrm {id} _{Y}$ («обратное справа»), называется сечением отображения $F$.

• Функция $F$ является обратной к $F^{-1}$:

$\left(F^{-1}\right)^{-1}=F$.

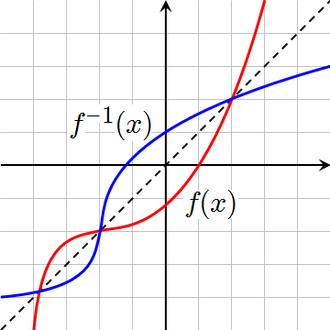
• Пусть $F:X\subset \mathbb {R} \to Y\subset \mathbb {R}$ — биекция. Пусть $F^{-1}:Y\to X$ её обратная функция. Тогда графики функций $y=F(x)$ и $y=F^{-1}(x)$ симметричны относительно прямой $y=x$.
• Также, если у функции $f(x)$ есть обратная ей $f^{-1}(x)$, то графики этих функций будут симметричны относительно линии $y=x$.

Теорема. Композиция любых двух обратимых функций является обратимой функцией, то есть ${\left(f\circ g\right)}^{-1}=g^{-1}\circ f^{-1}$.

Доказательство

Поскольку $\alpha \circ {\alpha }^{-1}=e$ и $\alpha \circ e=\alpha$ для любой обратимой функции $\alpha$, где $e$ — тождественное преобразование, то можно записать следующие равенства. Имеем: $e=e\Longleftrightarrow e=f\circ f^{-1}\Longleftrightarrow e=f\circ g\circ g^{-1}\circ f^{-1}\Longleftrightarrow e=\left(f\circ g\right)\circ \left(g^{-1}\circ f^{-1}\right).$ Подействуем слева функцией ${\left(f\circ g\right)}^{-1}$ и получим: ${\left(f\circ g\right)}^{-1}\circ \mid e={\left(f\circ g\right)}^{-1}\circ \left(f\circ g\right)\circ \left(g^{-1}\circ f^{-1}\right)\Longleftrightarrow {\left(f\circ g\right)}^{-1}\circ e=e\circ .$

Разложение в степенной ряд

Обратная функция аналитической в некоторой окрестности точки $x_{0}$ функции может быть представлена в виде степенного ряда:

$f^{-1}(y)=\sum _{k=0}^{\infty }A_{k}(x_{0}){\frac {(y-f(x_{0}))^{k}}{k!}},$

где функции $A_{k}$ задаются рекурсивной формулой:

$A_{n}(x)={\begin{cases}x\;,\;n=0\\{\frac {A_{n-1}'(x)}{f'(x)}}\;,\;n>0\end{cases}}$

См. также

• Теорема Лагранжа об обращении рядов
• Обратные тригонометрические функции
• Обратимая функция